The molární objem Jedná se o intenzivní vlastnost, která udává, kolik prostoru zabírá mol určité látky nebo sloučeniny. Představuje to symbol Vm, y je vyjádřeno v jednotkách dm3/ mol pro plyny a cm3/ mol pro kapaliny a pevné látky, protože ty jsou více omezeny vyššími mezimolekulárními silami.
Tato vlastnost se opakuje při studiu termodynamických systémů zahrnujících plyny; protože pro kapaliny a pevné látky rovnice určují Vm stávají se komplikovanějšími a nepřesnějšími. Pokud jde o základní kurzy, je tedy molární objem vždy spojen s teorií ideálního plynu..
To je způsobeno skutečností, že strukturální aspekty nejsou pro ideální nebo dokonalé plyny relevantní; všechny jeho částice jsou zobrazeny jako koule, které se navzájem pružně srazí a chovají se stejným způsobem bez ohledu na to, jaké jsou jejich hmotnosti nebo vlastnosti.
V tomto případě bude mol jakéhokoli ideálního plynu zaujímat při daném tlaku a teplotě stejný objem Vm. Potom se říká, že za normálních podmínek P a T, 1 atm, respektive 0 ° C, bude jeden mol ideálního plynu zaujímat objem 22,4 litru. Tato hodnota je užitečná a přibližná i při hodnocení skutečných plynů.
Rejstřík článků
Okamžitý vzorec pro výpočet molárního objemu druhu je:
PROTIm = V / n
Kde V je objem, který zabírá, a n množství druhu v krtcích. Problém je v tom, že Vm závisí na tlaku a teplotě, které molekuly zažívají, a je žádoucí matematický výraz, který zohledňuje tyto proměnné.
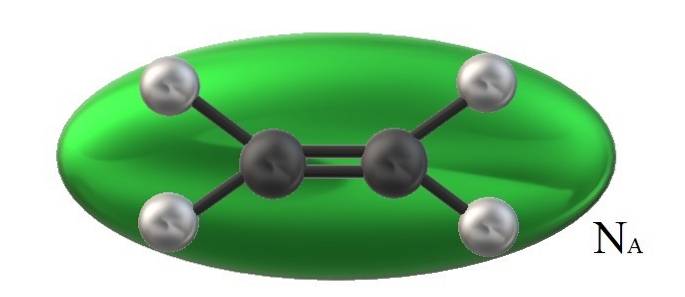
Ethylen na obrázku, HdvaC = CHdva, má přidružený molekulární objem omezený zeleným elipsoidem. Tento HdvaC = CHdva Může se otáčet několika způsoby, což je, jako by se uvedený elipsoid pohyboval v prostoru, aby si představil, jaký objem by zabral (zjevně zanedbatelný).
Pokud však objem takového zeleného elipsoidu vynásobíme NNA, Avogadrovo číslo, pak budeme mít jeden mol molekul ethylenu; jeden krtek elipsoidů vzájemně na sebe působí. Při vyšších teplotách se molekuly od sebe oddělí; zatímco pod vyšším tlakem se smrští a zmenší svůj objem.
Proto Vm je závislá na P a T. Ethylen má rovinnou geometrii, takže nelze předpokládat, že jeho Vm je přesně a přesně stejný jako u metanu, CH4, čtyřboká geometrie a může být reprezentována koulí a ne elipsoidem.
Molekuly nebo atomy kapalin a pevných látek mají také svůj vlastní Vm, což může zhruba souviset s jeho hustotou:
PROTIm = m / (dn)
Teplota ovlivňuje molární objem kapalin a pevných látek více než tlak, pokud se druhá mocně neliší nebo není přehnaná (v řádu GPa). Podobně, jak již bylo uvedeno u ethylenu, mají geometrie a molekulární struktury velký vliv na hodnoty Vm.
Za normálních podmínek se však pozoruje, že hustoty různých kapalin nebo pevných látek se příliš neliší ve svých velikostech; totéž platí pro jeho molární objemy. Všimněte si, že čím jsou hustší, tím menší bude Vm.
Pokud jde o pevné látky, jejich molární objem také závisí na jejich krystalických strukturách (objem jejich jednotkové buňky)..
Na rozdíl od kapalin a pevných látek existuje pro ideální plyny rovnice, která nám umožňuje vypočítat Vm jako funkce P a T a jejich změn; to je to ideálních plynů:
P = nRT / V
Což je vstřícné k vyjádření V / n:
V / n = RT / P
PROTIm = RT / P
Použijeme-li plynovou konstantu R = 0,082 L atm K-1Krtek-1, pak by teploty měly být vyjádřeny v kelvinech (K) a tlaky v atmosféře. Všimněte si, že zde vidíme, proč Vm je intenzivní vlastnost: T a P nemají nic společného s hmotou plynu, ale s jeho objemem.
Tyto výpočty jsou platné pouze za podmínek, kdy se plyny chovají téměř ideálně. Hodnoty získané experimentováním však mají ve srovnání s teoretickým malé rozpětí chyb.
Existuje plyn Y, jehož hustota je 8,5 · 10-4 g / cm3. Pokud máme 16 gramů, což odpovídá 0,92 molů Y, vypočítáme jeho molární objem.
Z vzorce hustoty můžeme vypočítat, jaký objem Y těchto 16 gramů zabírá:
V = 16 g / (8,5 10-4 g / cm3)
= 18,823,52 cm3 nebo 18,82 l
Takže Vm Vypočítává se přímo vydělením tohoto objemu počtem daných molů:
PROTIm = 18,82 l / 0,92 mol
= 20,45 l / mol nebo L mol-1 nebo dm3Krtek-1
V předchozím příkladu Y nebylo kdykoli uvedeno, jaká byla teplota, kterou částice uvedeného plynu zažívaly. Za předpokladu, že Y pracovalo za atmosférického tlaku, vypočítejte teplotu potřebnou k jeho komprimaci na stanovený molární objem.
Prohlášení o cvičení je delší než jeho rozlišení. Používáme rovnici:
PROTIm = RT / P
Ale řešíme pro T a protože víme, že atmosférický tlak je 1 atm, řešíme:
T = VmP / R
= (20,45 l / mol) (1 atm) / (0,082 l atm / K mol)
= 249,39 K.
To znamená, že jeden mol Y obsadí 20,45 litru při teplotě blízké -23,76 ° C.
Podle předchozích výsledků určete Vm při 0 ° C, 25 ° C a při absolutní nule při atmosférickém tlaku.
Při transformaci teplot na kelvin máme nejprve 273,17 K, 298,15 K a 0 K. Vyřešíme to přímo dosazením první a druhé teploty:
PROTIm = RT / P
= (0,082 l atm / K mol) (273,15 K) / 1 atm
= 22,40 l / mol (0 ° C)
= (0,082 l atm / K mol) (298,15 K) / 1 atm
= 24,45 l / mol (25 ° C)
Na začátku byla zmíněna hodnota 22,4 litru. Všimněte si, jak Vm se zvyšuje s teplotou. Když chceme udělat stejný výpočet s absolutní nulou, narazíme na třetí zákon termodynamiky:
(0,082 l atm / K mol) (0 K) / 1 atm
= 0 L / mol (-273,15 ° C)
Plyn Y nemůže mít neexistující molární objem; to znamená, že byl transformován na kapalinu a předchozí rovnice již není platná.
Na druhou stranu nemožnost výpočtu Vm při absolutní nule se řídí třetím zákonem termodynamiky, který říká, že je nemožné ochladit jakoukoli látku na teplotu absolutní nuly.
Zatím žádné komentáře