
Absorbance, co to je, příklady a řešená cvičení
The absorbance je logaritmus se záporným znaménkem kvocientu mezi intenzitou vznikajícího světla a intenzitou dopadajícího světla na vzorku průsvitného roztoku, který byl osvětlen monochromatickým světlem. Tento podíl je propustnost.
Fyzikální proces průchodu světla vzorkem se nazývá propustnost světla, a absorbance je jeho měřítkem. Z tohoto důvodu se absorbance stává nejmenším logaritmem propustnosti a je důležitým údajem pro stanovení koncentrace vzorku, který je obecně rozpuštěn v rozpouštědle, jako je voda, alkohol nebo jakékoli jiné..
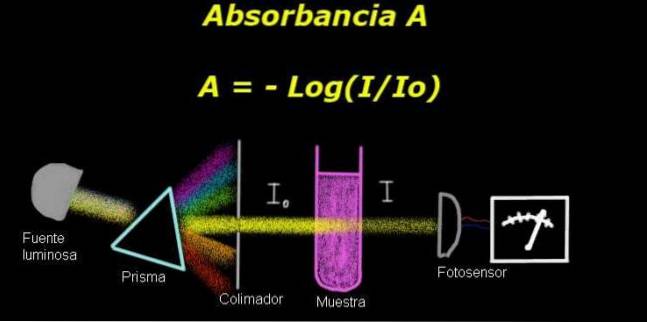
K měření absorbance potřebujete zařízení s názvem elektrofotometr, kterým se měří proud, který je úměrný intenzitě dopadajícího světla na jeho povrchu.
Při výpočtu propustnosti se obvykle nejprve měří signál intenzity odpovídající samotnému rozpouštědlu a tento výsledek se zaznamená jako Io.
Poté se rozpuštěný vzorek umístí do rozpouštědla za stejných světelných podmínek. Signál měřený elektro-fotometrem je označen jako Já, což umožňuje vypočítat propustnost T podle následujícího vzorce:
T = I / Inebo
Je to bezrozměrné množství. The absorbance A je tedy vyjádřen jako:
A = - log (T) = - log (I / Inebo)
Rejstřík článků
- 1 Molární absorbance a absorpční schopnost
- 1.1 Beer-Lambertův zákon
- 2 Příklady
- 2.1 Příklad 1
- 2.2 Příklad 2
- 3 Vyřešená cvičení
- 3.1 Cvičení 1
- 3.2 Cvičení 2
- 3.3 Cvičení 3
- 4 Odkazy
Molární absorbance a absorpční schopnost
Molekuly, které tvoří chemickou látku, jsou schopny absorbovat světlo a jedním z těchto ukazatelů je právě absorbance. Je výsledkem interakce mezi fotony a molekulárními elektrony.
Jedná se tedy o velikost, která bude záviset na hustotě nebo koncentraci molekul, které tvoří vzorek, a také na optické dráze nebo vzdálenosti ujeté světlem..
Experimentální údaje ukazují, že absorbance NA je lineárně úměrný koncentraci C a na dálku d prochází světlem. Takže pro výpočet na základě těchto parametrů lze stanovit následující vzorec:
A = ε⋅C⋅d
Ve výše uvedeném vzorci, ε je konstanta proporcionality známá jako molární nasákavost.
Molární nasákavost závisí na typu látky a vlnové délce, při které se měří absorbance. The molární nasákavost je také citlivý na teplotu vzorku a pH vzorku.
Beer-Lambertův zákon
Tento vztah mezi absorbancí, nasákavostí, koncentrací a vzdáleností tloušťky dráhy, kterou světlo ve vzorku následuje, je známý jako Beer-Lambertův zákon..

Zde je několik příkladů, jak ji používat.
Příklady
Příklad 1
Během experimentu je vzorek osvětlen červeným světlem z helium-neonového laseru, jehož vlnová délka je 633 nm. Elektrofotometr měří 30 mV při přímém dopadu laserového světla a 10 mV při průchodu vzorkem..
V tomto případě je propustnost:
T = I / Io = 10 mV / 30 mV = ⅓.
A absorbance je:
A = - log (⅓) = log (3) = 0,48
Příklad 2
Pokud je stejná látka umístěna do nádoby, která má poloviční tloušťku než ta, která byla použita v příkladu 1, uveďte, kolik označí elektrofotometr, když světlo z helium-neonového laseru projde vzorkem.
Je třeba vzít v úvahu, že pokud se tloušťka zmenší o polovinu, pak se absorbance, která je úměrná optické tloušťce, sníží o polovinu, tj. A = 0,28. Propustnost T bude dána následujícím vztahem:
T = 10-A = 10 ^ (- 0,28) = 0,53
Elektrofotometr bude číst 0,53 * 30 mV = 15,74 mV.
Vyřešená cvičení
Cvičení 1
Chceme určit molární nasákavost určité patentované sloučeniny, která je v roztoku. K tomu je roztok osvětlen světlem ze sodíkové výbojky 589 nm. Vzorek bude umístěn do držáku vzorku o tloušťce 1,50 cm.
Výchozím bodem je roztok s koncentrací 4,00 × 10 ^ -4 mol na litr a měří se propustnost, což vede k 0,06. Pomocí těchto údajů určete molární absorpční schopnost vzorku..
Řešení
Nejprve se určí absorbance, která je definována jako nejmenší logaritmus k základu deseti propustnosti:
A = - log (T)
A = - log (0,06) = 1,22
Poté se použije Lambert-Beerův zákon, který stanoví vztah mezi absorbancí, molární absorpcí, koncentrací a optickou délkou:
A = ε⋅C⋅d
Při řešení molární absorpce se získá následující vztah:
ε = A / (C⋅d)
dosazením daných hodnot máme:
ε = 1,22 / (4,00 × 10 ^ -4 M⋅1,5 cm) = 2030 (M⋅cm) ^ - 1
Výše uvedený výsledek byl zaokrouhlen na tři platné číslice.
Cvičení 2
Aby se zlepšila přesnost a určila chyba měření molární absorbance vzorku při cvičení 1, vzorek se postupně zředí na polovinu koncentrace a v každém případě se měří propustnost..
Počínaje Co = 4 × 10 ^ -4 M s propustností T = 0,06 se získá následující posloupnost dat pro propustnost a absorbance vypočtené z propustnosti:
Co / 1-> 0,06-> 1,22
Co / 2-> 0,25 -> 0,60
Co / 4-> 0,50 -> 0,30
Co / 8-> 0,71-> 0,15
Co / 16-> 0,83-> 0,08
Co / 32-> 0,93-> 0,03
Co / 64-> 0,95-> 0,02
Co / 128-> 0,98-> 0,01
Co / 256-> 0,99-> 0,00
S těmito daty proveďte:
a) Graf absorbance versus koncentrace.
b) Lineární přizpůsobení dat a najděte sklon.
c) Ze získané sklonu vypočítejte molární absorpční schopnost.
Řešení
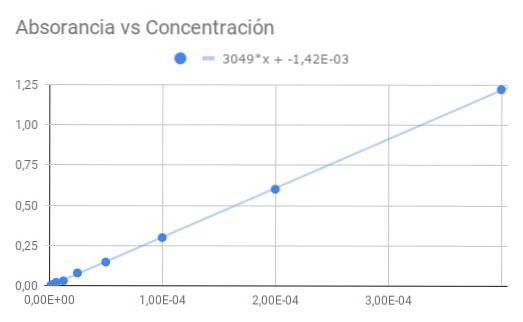
Získaný sklon je součinem molární absorpce a optické vzdálenosti, takže vydělením sklonu délkou 1,5 cm získáme molární absorpci
ε = 3049 / 1,50 = 2033 (M⋅cm) ^ - 1
Cvičení 3
S údaji z cvičení 2:
a) Vypočítejte absorpční schopnost pro každý údaj.
b) Určete průměrnou hodnotu molární absorbance, její směrodatnou odchylku a statistickou chybu spojenou s průměrem..
Řešení
Molární absorpční schopnost se vypočítá pro každou z testovaných koncentrací. Pamatujte, že světelné podmínky a optická vzdálenost zůstávají pevné.
Výsledky molární absorpce jsou:
2033, 2007, 2007, 1983, 2158, 1681, 2376, 1872, 1862 v jednotkách 1 / (M * cm).
Z těchto výsledků můžeme vzít průměrnou hodnotu:
<ε> = 1998 (M * cm) ^ - 1
Se standardní odchylkou: 184 (M * cm) ^ - 1
Střední chyba je směrodatná odchylka dělená druhou odmocninou počtu dat, tj.:
Δ<ε>= 184/9 ^ 0,5 = 60 (M * cm) ^ - 1
Nakonec se dospělo k závěru, že patentovaná látka má molární absorpční schopnost na frekvenci 589 nm produkovanou sodíkovou lampou:
<ε> = (2000 ± 60) (M * cm) ^ - 1
Reference
- Atkins, P. 1999. Fyzikální chemie. Edice Omega. 460-462.
- Průvodce. Propustnost a absorbance. Obnoveno z: quimica.laguia2000.com
- Toxikologie prostředí. Propustnost, absorbance a Lambertův zákon. Obnoveno z: repositorio.innovacionumh.es
- Fyzické dobrodružství. Absorbance a propustnost. Obnoveno z: rpfisica.blogspot.com
- Spektrofotometrie. Obnoveno z: chem.libretexts.org
- Toxikologie prostředí. Propustnost, absorbance a Lambertův zákon. Obnoveno z: repositorio.innovacionumh.es
- Wikipedia. Absorbance Obnoveno z: wikipedia.com
- Wikipedia. Spektrofotometrie. Obnoveno z: wikipedia.com



Zatím žádné komentáře