
Míra oblouku (geometrie), typy oblouků, příklady
The luk, v geometrii je to jakákoli zakřivená čára, která spojuje dva body. Zakřivená čára, na rozdíl od přímky, je čára, jejíž směr je v každém bodě na ní odlišný. Opakem oblouku je segment, protože se jedná o přímý úsek, který spojuje dva body.
Oblouk nejčastěji používaný v geometrii je oblouk obvodu. Jiné oblouky v běžném používání jsou parabolický oblouk, eliptický oblouk a oblouk trolejového vedení. Oblouková forma se také často používá v architektuře jako dekorativní prvek a konstrukční prvek. To je případ překladů dveří a oken, stejně jako mostů a akvaduktů.

Rejstřík článků
- 1 Oblouk a jeho míra
- 2 typy luků
- 2.1 Kruhový oblouk
- 2.2 Parabolický oblouk
- 2.3 Obloukový oblouk
- 2.4 Eliptický oblouk
- 3 Příklady oblouků
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 Odkazy
Luk a jeho míra
Míra oblouku je jeho délka, která závisí na typu křivky, která spojuje dva body, a na jejich umístění..
Délka kruhového oblouku je jednou z nejjednodušších k výpočtu, protože je známa délka celého oblouku nebo obvodu obvodu.
Obvod kruhu jsou dva pi krát vaše rádio: p = 2 π R. S tímto vědomím, pokud chcete vypočítat délku s kruhového úhlového oblouku α (měřeno v radiánech) a poloměr R, použije se poměr:
(s / p) = (α / 2 π)
Pak vyčištění s z předchozího výrazu a dosazení obvodu p vyjádřením jako funkce poloměru R, ty máš:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R..
To znamená, že míra kruhového oblouku je součinem jeho úhlových otevíracích časů poloměru kruhového oblouku.
Pro oblouk obecně je problém komplikovanější, až do té míry, že velcí myslitelé starověku potvrdili, že to byl nemožný úkol..
Až příchod diferenciálního a integrálního počtu v roce 1665 byl problém měření jakéhokoli oblouku uspokojivě vyřešen.
Před vynálezem diferenciálního počtu bylo možné najít řešení pouze pomocí polygonálních čar nebo obvodových oblouků, které se přibližovaly skutečnému oblouku, ale tato řešení nebyla přesná.
Druhy luky
Z hlediska geometrie jsou oblouky klasifikovány podle zakřivené čáry, která spojuje dva body v rovině. Existují i další klasifikace podle jejich použití a architektonické formy.
Kruhový oblouk
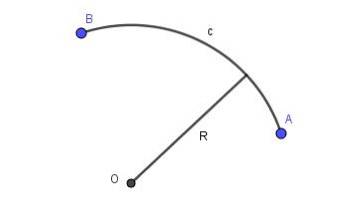
Když přímka spojující dva body roviny je kusem obvodu o určitém poloměru, máme kruhový oblouk. Obrázek 2 ukazuje kruhový oblouk c poloměru R spojovacích bodů A a B.
Parabolický oblouk
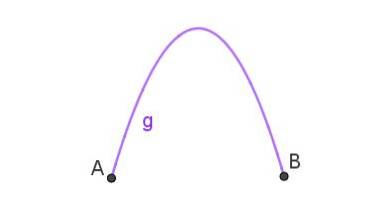
Parabola je cesta, po které následuje předmět, který byl šikmo vyhozen do vzduchu. Když je křivka, která spojuje dva body, parabola, máme parabolický oblouk jako ten, který je znázorněn na obrázku 3.
Toto je tvar paprsku vody, který vychází z hadice směřující nahoru. Ve vodních zdrojích lze pozorovat parabolický oblouk.

Catenary arch
Obloukový řetěz je další přirozený oblouk. Trolejové vedení je křivka, která se přirozeně tvoří, když řetěz nebo lano visí volně ze dvou samostatných bodů.
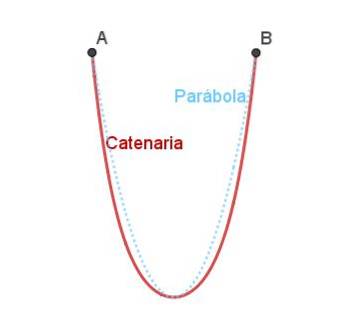
Řetězec je podobný parabole, ale není úplně stejný, jak je vidět na obrázku 4.
Obrácený řetězový oblouk se v architektuře používá jako konstrukční prvek s vysokou pevností v tlaku. Ve skutečnosti se může ukázat jako nejsilnější typ oblouku ze všech možných forem..
Chcete-li vytvořit pevný oblouk trolejového vedení, stačí zkopírovat tvar visícího lana nebo řetězu, poté se kopírovaný tvar převrátí, aby se reprodukoval na překladu dveří nebo oken.
Eliptický oblouk
Oblouk je eliptický, pokud je křivka spojující dva body částí nebo částí elipsy. Elipsa je definována jako lokus bodů, jejichž vzdálenost ke dvěma daným bodům vždy přidává konstantní množství.
Elipsa je křivka, která se objevuje v přírodě: je to křivka trajektorie planet kolem Slunce, jak prokázal Johannes Kepler v roce 1609.
V praxi lze elipsu nakreslit připnutím dvou vzpěr k zemi nebo dvou kolíků na papíře a uvázáním provázku k nim. Poté je lano napnuto značkovačem nebo tužkou a je sledována křivka. Kus elipsy je eliptický oblouk. Následující animace ukazuje, jak je nakreslena elipsa:
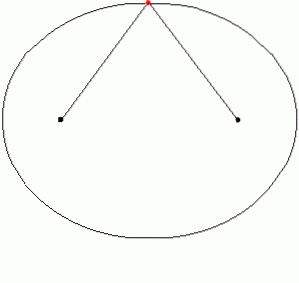
Obrázek 6 ukazuje spojovací body eliptického oblouku G a H.
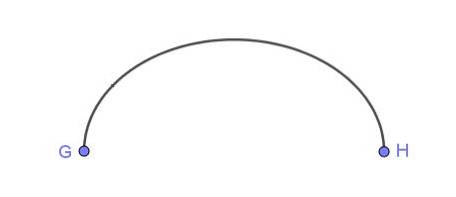
Příklady oblouků
Následující příklady odkazují na to, jak vypočítat obvod některých konkrétních oblouků.
Příklad 1
Obrázek 7 ukazuje okno zakončené řezaným kruhovým obloukem. Rozměry zobrazené na obrázku jsou ve stopách. Vypočítejte délku oblouku.
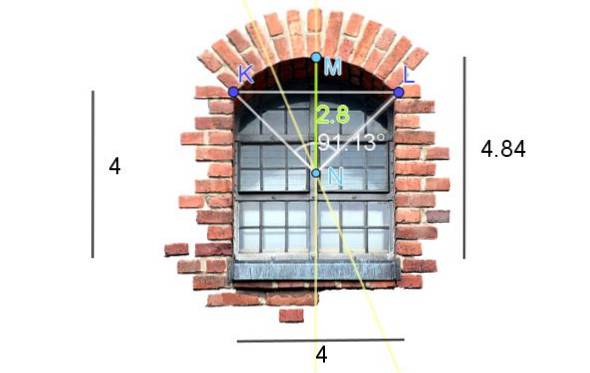
Pro získání středu a poloměru kruhového oblouku okenního překladu jsou na obrázku vytvořeny následující konstrukce:
-Nakreslí se segment KL a nakreslí se jeho půlení.
-Poté je umístěn nejvyšší bod překladu, který nazýváme M. Dále je uvažován segment KM a je sledována jeho prostřední čára..
Průsečík dvou půlících čar je bod N a je také středem kruhového oblouku.
-Nyní musíme změřit délku segmentu NM, který se shoduje s poloměrem R kruhového oblouku: R = 2,8 stopy.
-Chcete-li znát délku oblouku kromě poloměru, je nutné znát úhel, který oblouk tvoří. Což lze určit dvěma metodami, buď se měří úhloměrem, nebo se alternativně počítá pomocí trigonometrie.
V zobrazeném případě je úhel tvořený obloukem 91,13 °, který musí být převeden na radiány:
91,13 ° = 91,13 ° * π / 180 ° = 1,59 radiánů
Nakonec vypočítáme délku s oblouku pomocí vzorce s = αR.
s = 1,59 * 2,8 stopy = 4,45 stopy
Příklad 2
Najděte délku eliptického oblouku zobrazeného na obrázku 8 a znáte hlavní poloosu r a poloviční vedlejší osa s elipsy.
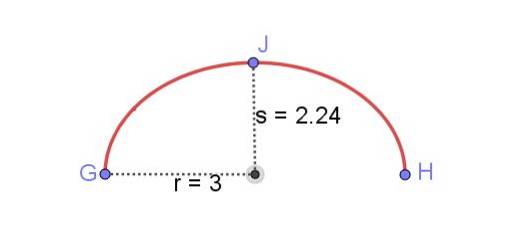
Nalezení délky elipsy bylo po dlouhou dobu jedním z nejobtížnějších problémů v matematice. Můžete získat řešení vyjádřená eliptickými integrály, ale abyste měli číselnou hodnotu, musíte tyto integrály rozšířit v mocninných řadách. Přesný výsledek by vyžadoval nekonečné množství těchto řad.
Naštěstí hinduistický matematický génius Ramanujan, který žil v letech 1887 až 1920, našel vzorec, který se velmi přesně přibližuje obvodu elipsy:
Obvod elipsy = π [3 (r + s) - √ ((3r + s) (r + 3s))]
Obvod elipsy r = 3 cm as = 2,24 cm je 16,55 cm. Zobrazený eliptický oblouk má však poloviční hodnotu:
Délka eliptického oblouku GH = 8,28 cm.
Reference
- Clemens S. 2008. Geometrie a trigonometrie. Pearson Education.
- García F. Numerické procedury v Javě. Délka elipsy. Obnoveno z: sc.ehu.es
- Dynamická geometrie. Luky. Obnoveno z geometriadinamica.es
- Piziadas. Elipsy a paraboly kolem nás. Obnoveno z: piziadas.com
- Wikipedia. Oblouk (geometrie). Obnoveno z: es.wikipedia.com



Zatím žádné komentáře