
Neelastické pády v jedné dimenzi a příklady
The nepružné šoky nebo nepružné srážky jsou krátká a intenzivní interakce mezi dvěma objekty, ve kterých je zachována hybnost, ale ne kinetická energie, jejíž procento je transformováno na nějaký jiný typ energie.
Havárie nebo kolize jsou v přírodě časté. Subatomové částice se srazí extrémně vysokou rychlostí, zatímco mnoho sportů a her spočívá v neustálých srážkách. I galaxie jsou schopné srážky.

Ve skutečnosti je hybnost zachována při jakémkoli typu srážky, pokud srážející se částice tvoří izolovaný systém. V tomto smyslu tedy není žádný problém. Nyní mají objekty kinetickou energii spojenou s pohybem, který mají. Co se s touto energií může stát při srážce??
Vnitřní síly, ke kterým dochází při srážce mezi objekty, jsou silné. Když je uvedeno, že kinetická energie není konzervována, znamená to, že je transformována na jiné druhy energie: například na energii zvukovou (spektakulární srážka má charakteristický zvuk).
Další možnosti využití kinetické energie: třecí teplo a samozřejmě nevyhnutelná deformace, kterou objekty při srážce procházejí, například karoserie automobilů na obrázku výše.
Rejstřík článků
- 1 Příklady nepružných kolizí
- 2 Dokonale nepružné kolize v jedné dimenzi
- 3 Koeficient restituce
- 4 Jak určit restituční koeficient?
- 5 Pracované příklady
- 5.1 - Cvičení 1
- 5.2 - Cvičení 2
- 5.3 - Cvičení 3
- 6 Reference
Příklady nepružných kolizí
- Dvě masy plastelíny se srazily a slepily, pohybovaly se jako jeden kus po srážce.
- Gumový míč, který se odrazí od stěny nebo podlahy. Míč se deformuje, když narazí na povrch.
Ne celá kinetická energie se až na několik výjimek transformuje na jiné druhy energie. Objekty si mohou udržet určité množství této energie. Později uvidíme, jak vypočítat procento.
Když se srážející se kousky drží pohromadě, kolize se nazývá dokonale nepružná a oba mají tendenci se nakonec pohybovat společně..
Dokonale nepružné kolize v jedné dimenzi
Kolize na obrázku ukazuje dva objekty různých hmot m1 Y mdva, pohybující se k sobě rychlostí protii1 Y protii2 resp. Všechno se děje na horizontále, to znamená, že jde o kolizi v jedné dimenzi, kterou je nejsnadněji studovat.
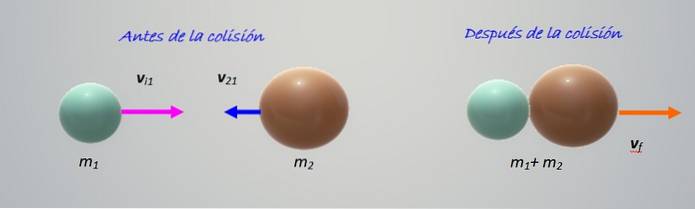
Objekty se srazí a poté se pohybem doprava slepí. Jedná se o dokonale nepružnou kolizi, takže musíme pouze udržet dynamiku:
Pnebo = PF
Hybnost je vektor, jehož jednotky SI jsou N.s. V popsané situaci lze od vektorového zápisu upustit při řešení kolizí v jedné dimenzi:
mvnebo = mvF
Hybnost systému je vektorový součet hybnosti každé částice.
m1 protii1 + mdva protii2 = (m1 + mdva) vF
Konečná rychlost je dána vztahem:
protiF = (m1 protii1 + mdva protii2) / (m1 + mdva)
Koeficient restituce
Existuje množství, které může naznačovat, jak pružná je kolize. Je to o koeficient restituce, který je definován jako záporný kvocient mezi relativní rychlostí částic po srážce a relativní rychlostí před srážkou.
Ať u1 a udva příslušné rychlosti částic zpočátku. A buďte v1 a Vdva příslušné konečné rychlosti. Matematicky lze koeficient restituce vyjádřit takto:
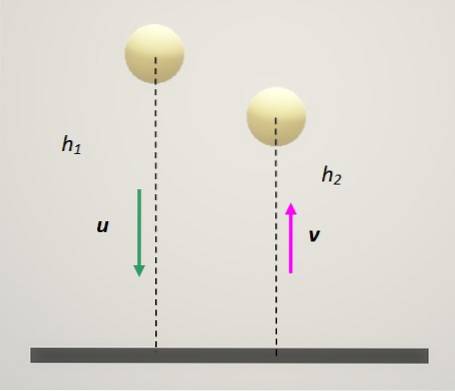
- Pokud ε = 0, je to ekvivalentní potvrzení, že vdva = v1. To znamená, že konečné rychlosti jsou stejné a kolize je nepružná, jako je ta popsaná v předchozí části..
- Když ε = 1, znamená to, že se relativní rychlosti před i po srážce nezmění, v tomto případě je srážka elastická.
- A pokud 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
Jak určit restituční koeficient?
Koeficient restituce závisí na třídě materiálů zapojených do srážky. Velmi zajímavým testem k určení, jak pružný je materiál pro výrobu koulí, je pád koule na pevnou plochu a měření výšky odrazu.

V tomto případě má pevná deska vždy rychlost 0. Pokud je jí přiřazen index 1 a index koule 2 je:
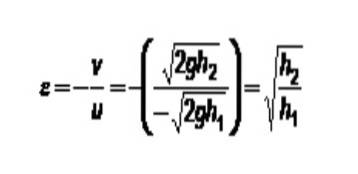



Na začátku bylo navrženo, že veškerá kinetická energie může být přeměněna na jiné druhy energie. Koneckonců, energie není zničena. Je možné, že se pohybující se objekty srazí a spojí a vytvoří jediný objekt, který se náhle zastaví? To není tak snadné si představit.
Představme si však, že se to děje naopak, jako ve filmu viděném v opačném směru. Objekt byl tedy zpočátku v klidu a poté explodoval a roztříštil se na různé části. Tato situace je zcela možná: jedná se o výbuch.
Explozi lze tedy považovat za dokonale nepružnou kolizi při pohledu zpět v čase. Hybnost je také zachována a lze konstatovat, že:
Pnebo = PF
Pracoval příklady
-Cvičení 1
Z měření je známo, že koeficient restituce oceli je 0,90. Ocelová koule spadne z výšky 7 m na pevnou desku. Vypočítat:
a) Jak vysoko se odrazí.
b) Jak dlouho trvá mezi prvním kontaktem s povrchem a druhým.
Řešení
a) Použije se rovnice, která byla odvozena dříve v části o stanovení restitučního koeficientu:
Výška je vyklizena hdva:
0,90dva . 7 m = 5,67 m
b) Aby mohla stoupat 5,67 metru, je vyžadována rychlost daná:


t max = vnebo/ g = (10,54 / 9,8 s) = 1,08 s.
Čas potřebný k návratu je stejný, proto je celkový čas na vylezení 5,67 metrů a návrat do výchozího bodu dvojnásobek maximálního času:
tlet = 2,15 s.
-Cvičení 2
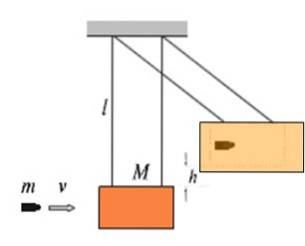
Obrázek ukazuje blok dřeva o hmotnosti M visící v klidu strunami délky l jako kyvadlo. Toto se nazývá balistické kyvadlo a používá se k měření rychlosti v vstupu do střely o hmotnosti m. Čím vyšší je rychlost, jakou kulka zasáhne blok, tím vyšší h bude stoupat.
Kulka v obrázku je vložena do bloku, jedná se tedy o naprosto nepružný šok.

Předpokládejme, že kulka o hmotnosti 9,72 g zasáhne blok hmotnosti 4,60 kg, potom sestava stoupne z rovnováhy o 16,8 cm. Jaká je rychlost proti z kulky?
Řešení
Během srážky je hybnost zachována a neboF je rychlost celku, jakmile se kulka vloží do bloku:
Pnebo = PF
Blok je zpočátku v klidu, zatímco střela míří na cíl rychlostí proti:
m.v + M.0 = (m + M) uF
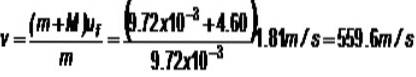
Neznámý neboF stále, ale po srážce je mechanická energie zachována, což je součet gravitační potenciální energie U a kinetické energie K:
Počáteční mechanická energie = konečná mechanická energie
Amo = Emf
NEBOnebo + K.nebo = UF + K.F
Gravitační potenciální energie závisí na výšce, do které souprava dosáhne. Pro rovnovážnou polohu je počáteční výška výškou považovanou za referenční úroveň, proto:
NEBOnebo = 0
Díky střele má celek kinetickou energii K.nebo, který se převede na gravitační potenciální energii, když souprava dosáhne své maximální výšky h. Kinetická energie je dána vztahem:
K = ½ mvdva
Kinetická energie je zpočátku:
K.nebo = (1/2) (M + m) uFdva
Pamatujte, že kulka a blok již tvoří jeden hromadný objekt M + m. Gravitační potenciální energie, když dosáhnou své maximální výšky, je:
NEBOF = (m + M) gh
Proto:
K.nebo = UF
(1/2) (M + m) uFdva = (m + M) gh
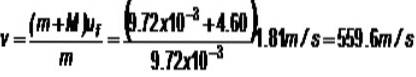
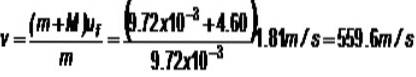
-Cvičení 3
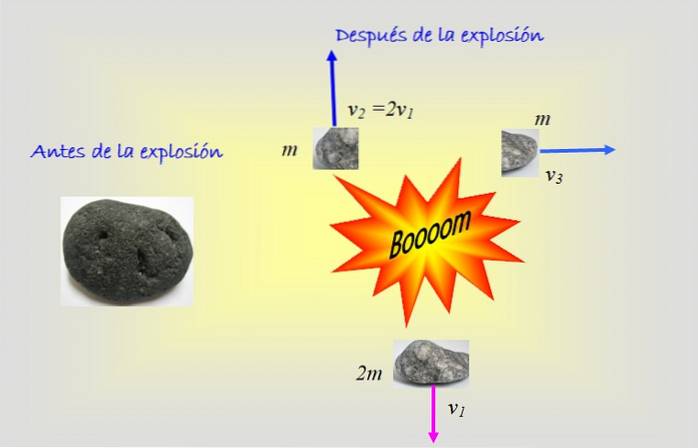
Objekt na obrázku exploduje do tří fragmentů: dva o stejné hmotnosti m a větší o hmotnosti 2 m. Obrázek ukazuje rychlosti každého fragmentu po výbuchu. Jaká byla počáteční rychlost objektu?
Řešení
V tomto problému je vyžadováno použití dvou souřadnic: X a Y, protože dva fragmenty mají vertikální rychlosti, zatímco zbytek má horizontální rychlost.
Celková hmotnost objektu je součtem hmotnosti všech fragmentů:
M = m + m + 2m = 4m
Hybnost je zachována jak v ose x, tak v ose y, je uvedena samostatně:
- 4 m. neboX= m v3
- 4 m. neboY = m. 2v1 - 2 m. proti1
Všimněte si, že velký fragment se pohybuje dolů rychlostí v1, což naznačuje, že na něj byla umístěna záporná značka.
Z druhé rovnice to okamžitě vyplývá neboY = 0, a od prvního se ux okamžitě vymaže:

Reference
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6th. Sál Eda Prentice. 175-181
- Rex, A. 2011. Základy fyziky. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Základy fyziky. 9na Cengage Learning. 172-182
- Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vyd. Svazek 1. Redakční reverté. 217-238
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. MacGraw Hill. 185-195



Zatím žádné komentáře