
Proces Braytonova cyklu, efektivita, aplikace, cvičení
The Braytonův cyklus je termodynamický cyklus, který se skládá ze čtyř procesů a je aplikován na stlačitelnou termodynamickou tekutinu, jako je plyn. Jeho první zmínka pochází z konce 18. století, ačkoli to bylo nějakou dobu předtím, než ji poprvé vznesl James Joule. Proto je také známý jako Jouleův cyklus..
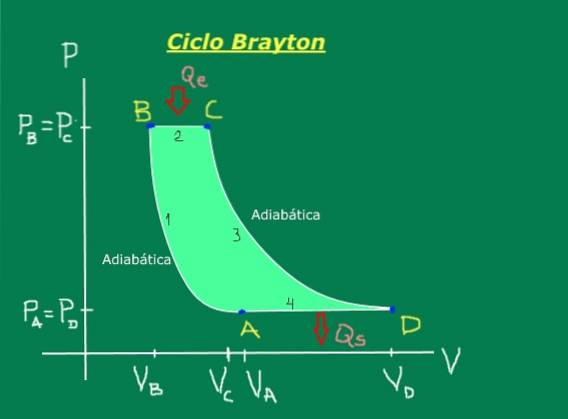
Skládá se z následujících stupňů, které jsou výhodně ilustrovány v diagramu tlaku a objemu na obrázku 1: adiabatická komprese (nedochází k výměně tepla), izobarická expanze (dochází při konstantním tlaku), adiabatická expanze (nedochází k výměně tepla) a izobarická komprese (nastává při konstantním tlaku).
Rejstřík článků
- 1 Proces a popis
- 1.1 Vstupné
- 1.2 Komprese
- 1.3 Spalování
- 1.4 Rozšíření
- 1.5 Výfuk
- 2 Účinnost jako funkce teploty, tepla a tlaku
- 2.1 Vstupní teplo, odchozí teplo a účinnost
- 2.2 Teplo a tlak v Braytonově cyklu
- 2.3 Zjednodušený výsledek
- 2.4 Účinnost jako funkce tlakového poměru
- 3 Aplikace
- 4 Vyřešená cvičení
- 4.1 - Cvičení 1
- 4.2 - Cvičení 2
- 5 Reference
Postup a popis
Braytonův cyklus je ideální termodynamický cyklus, který se nejlépe aplikuje na vysvětlení termodynamického provozu plynových turbín a směsi vzduch-palivo, používaných k výrobě elektrické energie a v leteckých motorech.
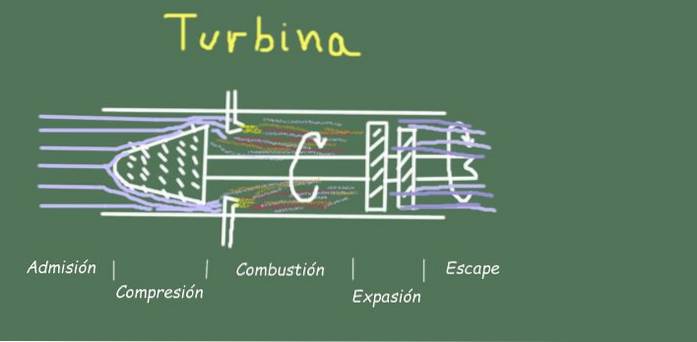
Například při provozu turbíny existuje několik stupňů v proudu provozního plynu, které uvidíme níže.
Přijetí
Skládá se ze vstupu vzduchu při okolní teplotě a tlaku vstupním otvorem turbíny.
Komprese
Vzduch je stlačován otáčením lopatek proti pevným lopatkám v kompresorové části turbíny. Tato komprese je tak rychlá, že nedochází prakticky k žádné výměně tepla, takže je modelována adiabatickým procesem AB Braytonova cyklu. Vzduch na výstupu z kompresoru zvýšil svůj tlak a teplotu.
Spalování
Vzduch se mísí s propanovým plynem nebo práškovým palivem, které se přivádí vstřikovači spalovací komory. Směs produkuje chemickou reakci spalování.
Tato reakce zajišťuje teplo, které zvyšuje teplotu a kinetickou energii plynných částic, které expandují ve spalovací komoře za konstantního tlaku. V Braytonově cyklu je tento krok modelován pomocí procesu BC, ke kterému dochází při konstantním tlaku.
Rozšíření
V části samotné turbíny vzduch pokračuje v expanzi proti lopatkám turbíny, což způsobuje její otáčení a produkci mechanické práce. V tomto kroku vzduch snižuje svoji teplotu, ale prakticky nevyměňuje teplo s okolním prostředím..
V Braytonově cyklu je tento krok simulován jako proces adiabatické expanze CD. Část práce turbíny se přenáší do kompresoru a druhá se používá k pohonu generátoru nebo vrtule.
Uniknout
Odcházející vzduch má konstantní tlak, který se rovná tlaku okolního prostředí a přenáší teplo na obrovské množství vnějšího vzduchu, takže v krátké době přebírá stejnou teplotu jako vstupní vzduch. V Braytonově cyklu je tento krok simulován procesem DA s konstantním tlakem, který uzavírá termodynamický cyklus.
Účinnost jako funkce teploty, tepla a tlaku
Navrhujeme vypočítat účinnost Braytonova cyklu, pro kterou vycházíme z jeho definice.
V tepelném motoru je účinnost definována jako čistá práce vykonaná strojem dělená dodanou tepelnou energií.

První princip termodynamiky uvádí, že čisté teplo přispívající k plynu v termodynamickém procesu se rovná změně vnitřní energie plynu plus jeho práci..
Ale v úplném cyklu je variace vnitřní energie nulová, takže čisté teplo přispívající do cyklu se rovná čisté odvedené práci..

Vstupní teplo, odchozí teplo a účinnost
Předchozí výraz nám umožňuje zapsat účinnost jako funkci absorbovaného nebo příchozího tepla Qe (pozitivní) a přeneseného nebo odchozího tepla Qs (negativní).

Teplo a tlak v Braytonově cyklu
V Braytonově cyklu vstupuje teplo do izobarického procesu BC a vystupuje v izobarickém procesu DA.
Za předpokladu, že n molů plynu při konstantním tlaku je zásobováno citelným teplem Qe v procesu BC, pak se jeho teplota zvyšuje z Tb na Tc podle následujícího vztahu:

Odchozí teplo Qs lze vypočítat podobně podle následujícího vztahu, který platí pro proces konstantního tlaku DA:

Dosazením těchto výrazů do výrazu, který nám dává účinnost jako funkci příchozího a odchozího tepla, což usnadňuje příslušná zjednodušení, se získá následující vztah k účinnosti:

Zjednodušený výsledek
Pokud vezmeme v úvahu to, je možné předchozí výsledek zjednodušit Pa = Pd No a co Pb = Pc protože procesy AD a BC jsou izobarické, tj. při stejném tlaku.
Kromě toho, protože procesy AB a CD jsou adiabatické, je Poissonův poměr splněn pro oba procesy:

Kde gama představuje adiabatický kvocient, tj. kvocient mezi tepelnou kapacitou při konstantním tlaku a tepelnou kapacitou při konstantním objemu.
Pomocí těchto vztahů a vztahu z rovnice stavu ideálního plynu můžeme získat alternativní výraz pro Poissonův poměr:

Jak to víme Pa = Pd No a co Pb = Pc dosazením a dělením prutu prutem získáme následující vztah mezi teplotami:

Pokud je každý člen předchozí rovnice odečten jednotkou, rozdíl je vyřešen a termíny jsou uspořádány, lze ukázat, že:


Výkon jako funkce tlakového poměru
Výraz získaný pro účinnost Braytonova cyklu jako funkce teplot lze přepsat tak, aby byl formulován jako funkce kvocientu tlaku na výstupu a vstupu kompresoru.
Toho je dosaženo, pokud je Poissonův poměr mezi body A a B známý jako funkce tlaku a teploty, přičemž se účinnost cyklu vyjadřuje takto:

Typický tlakový poměr je 8. V tomto případě má Braytonův cyklus teoretický výtěžek 45%..
Aplikace
Braytonův cyklus jako model se aplikuje na plynové turbíny, které se používají v termoelektrických zařízeních, aby se pohnuly generátory vyrábějícími elektřinu.
Jde také o teoretický model, který je vhodný pro provoz turbovrtulových motorů používaných v letadlech, ale v proudových motorech letadel je vůbec nepoužitelný..
Pokud chcete maximalizovat práci produkovanou turbínou na přesunutí generátorů nebo vrtulí letounu, použije se Braytonův cyklus..

Na druhé straně v proudových motorech letadel není zajímavé převádět kinetickou energii spalin na produkci práce, která by stačila k dobití turbodmychadla.
Naopak je důležité získat nejvyšší možnou kinetickou energii vypuzeného plynu, aby se podle principu akce a reakce získala hybnost letadla..
Vyřešená cvičení
-Cvičení 1
Plynová turbína používaná v termoelektrických elektrárnách má tlak na výstupu kompresoru 800 kPa. Vstupní teplota plynu je okolní a je 25 stupňů Celsia a tlak je 100 kPa.
Ve spalovací komoře teplota stoupá až na 1027 Celsia, aby mohla vstoupit do turbíny.
Určete účinnost cyklu, teplotu plynu na výstupu z kompresoru a teplotu plynu na výstupu z turbíny.
Řešení
Protože máme tlak plynu na výstupu z kompresoru a víme, že vstupní tlak je atmosférický, je možné získat tlakový poměr:
r = Pb / Pa = 800 kPa / 100 KPa = 8
Vzhledem k tomu, že plyn, s nímž turbína pracuje, je směsí vzduchu a propanového plynu, použije se adiabatický koeficient pro diatomický ideální plyn, tj. Gama 1,4.
Účinnost by se pak počítala takto:
Tam, kde jsme použili vztah, který udává účinnost Braytonova cyklu jako funkce tlakového poměru v kompresoru.

Výpočet teploty
Pro stanovení teploty na výstupu z kompresoru nebo stejné teploty, s jakou plyn vstupuje do spalovací komory, použijeme vztah účinnosti s teplotou na vstupu a výstupu kompresoru.
Pokud z tohoto výrazu vyřešíme teplotu Tb, získáme:

Jako údaje pro cvičení máme, že po spalování teplota stoupne na 1027 Celsia, aby vstoupila do turbíny. Část tepelné energie plynu se používá k pohybu turbíny, takže teplota na jejím výstupu musí být nižší.
Pro výpočet teploty na výstupu z turbíny použijeme vztah mezi teplotou získanou dříve:

Odtud vyřešíme pro Td získání teploty na výstupu z turbíny. Po provedení výpočtů je získaná teplota:
Td = 143,05 Celsia.
-Cvičení 2
Po Braytonově cyklu následuje plynová turbína. Poměr tlaku mezi vstupem a výstupem kompresoru je 12.
Předpokládejte okolní teplotu 300 K. Jako další údaje je známo, že teplota plynu po spalování (před vstupem do turbíny) je 1 000 K.
Určete teplotu na výstupu z kompresoru a teplotu na výstupu z turbíny. Určete také, kolik kilogramů plynu obíhá turbínou za každou sekundu, protože jeho výkon je 30 KW.
Předpokládejme specifické teplo plynu jako konstantní a vezměte jeho hodnotu při pokojové teplotě: Cp = 1,0035 J / (kg K).
Předpokládejme také, že účinnost komprese v kompresoru a účinnost dekomprese v turbíně je 100%, což je idealizace, protože v praxi vždy dochází ke ztrátám..
Řešení
Abychom určili teplotu na výstupu kompresoru, protože známe teplotu na vstupu, musíme si uvědomit, že se jedná o adiabatickou kompresi, takže Poissonův poměr lze použít pro proces AB.



U jakéhokoli termodynamického cyklu se síťová práce bude vždy rovnat čistému teplu vyměněnému v cyklu..

Čistou práci na pracovní cyklus lze poté vyjádřit jako funkci hmotnosti plynu, který v tomto cyklu cirkuloval, a teplot.

V tomto výrazu m je množství plynu, které cirkuluje turbínou v jednom pracovním cyklu a Str měrné teplo.
Vezmeme-li derivaci s ohledem na čas předchozího výrazu, získáme čistou střední mocninu jako funkci hmotnostního toku.

Čistí se m bod, a dosazením teplot, výkonu a tepelné kapacity plynu získáme hmotnostní tok 1578,4 kg / s.
Reference
- Alfaro, J. Termodynamické cykly. Obnoveno z: fis.puc.cl.
- Fernandez J.F. Braytonův cyklus. Plynová turbína. U.T.N. (Mendoza). Obnoveno z: edutecne.utn.edu.ar.
- Sevillská univerzita. Fyzikální oddělení. Braytonův cyklus. Obnoveno z: laplace.us.es.
- Táchira National Experimental University. Přepravní jevy. Plynové energetické cykly. Obnoveno z: unet.edu.ve.
- Wikipedia. Braytonův cyklus. Obnoveno z: wikiwand.com
- Wikipedia. Plynová turbína. Obnoveno z: wikiwand.com.



Zatím žádné komentáře