
Stlačitelnost pevných látek, kapalin, plynů, příklady
The stlačitelnost látky nebo materiálu je změna objemu, kterou zažívá, když je vystavena změně tlaku. Obecně se objem snižuje, když se na systém nebo objekt aplikuje tlak. Někdy se však stane pravý opak: změna tlaku může způsobit explozi, při které systém zvětší objem nebo dojde k fázové změně..
V některých chemických reakcích k tomu může dojít a také v plynech, protože s rostoucí frekvencí kolizí dochází k odpudivým silám..

Když si představujete, jak snadné nebo obtížné může být komprimování objektu, zvažte tři stavy, ve kterých je hmota normálně: pevná látka, kapalina a plyn. V každém z nich si molekuly udržují určité vzájemné vzdálenosti. Čím silnější jsou vazby, které spojují molekuly látky tvořící předmět, a čím jsou blíže, tím obtížnější bude deformace.
Pevná látka má své molekuly velmi blízko u sebe, a když se je snaží přiblížit, objeví se odpudivé síly, které úkol ztěžují. Proto se říká, že pevné látky nejsou příliš stlačitelné. V molekulách kapalin je více prostoru, takže jejich stlačitelnost je větší, ale i tak změna objemu obvykle vyžaduje velké síly.
Pevné látky a kapaliny jsou tedy těžko stlačitelné. K dosažení znatelné změny objemu za takzvaných normálních tlakových a teplotních podmínek by bylo zapotřebí velmi velké změny tlaku. Na druhé straně jsou plyny, protože jejich molekuly jsou velmi vzdálené, snadno stlačitelné a dekomprimované.
Rejstřík článků
- 1 Stlačitelnost pevných látek
- 1.1 - Stlačitelnost materiálu
- 2 Vyřešená cvičení - příklady
- 2.1 - Vyřešené cvičení 1
- 2.2 - Vyřešené cvičení 2
- 2.3 - Vyřešené cvičení 3
- 3 Stlačitelnost v plynech
- 3.1 - Vyřešené cvičení 5
- 4 Odkazy
Pevná stlačitelnost
Když je předmět ponořen například do kapaliny, vyvíjí na něj tlak ve všech směrech. Tímto způsobem si můžeme myslet, že se objem objektu sníží, i když ve většině případů to nebude znatelné..
Situaci lze vidět na následujícím obrázku:
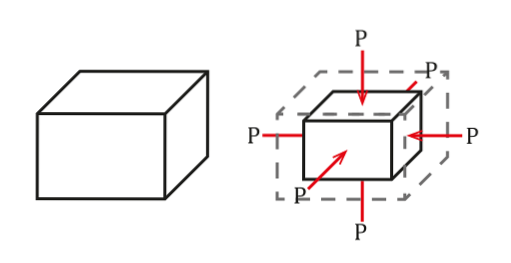
Tlak je definován jako síla na jednotku plochy, která způsobí změnu objemu ΔV úměrnou počátečnímu objemu objektu Vnebo. Tato změna objemu bude záviset na jeho kvalitách..
Hookeův zákon stanoví, že deformace, kterou objekt zažívá, je úměrná namáhání, které na něj působí:
Stres - napětí
Objemová deformace, kterou těleso zažívá, se kvantifikuje pomocí B požadované konstanty úměrnosti, která se nazývá objemový modul materiálu:
B = -pnutí / napětí
B = -ΔP / (ΔV / Vnebo)
Jako ΔV / Vnebo je bezrozměrná veličina, protože jde o kvocient mezi dvěma objemy, volumetrický modul má stejné jednotky tlaku, což jsou v mezinárodním systému Pascaly (Pa).
Záporné znaménko označuje očekávané snížení objemu, když je objekt dostatečně komprimován, to znamená, že se zvyšuje tlak.
-Stlačitelnost materiálu
Inverzní nebo převrácená hodnota objemového modulu je známá jako stlačitelnost a je označen písmenem k. Proto:

Tady k je záporná frakční změna objemu na zvýšení tlaku. Jeho jednotkami v mezinárodním systému jsou inverze Pa, tj. Mdva / N.
Rovnice pro B nebo pro k, pokud chcete, platí pro pevné látky i kapaliny. Koncept objemového modulu se u plynů používá jen zřídka. Níže je vysvětlen jednoduchý model pro kvantifikaci snížení objemu, se kterým může skutečný plyn zažít..
Rychlost zvuku a modul stlačitelnosti
Zajímavou aplikací je rychlost zvuku v médiu, která závisí na jeho modulu stlačitelnosti:

Vyřešená cvičení - příklady
-Vyřešené cvičení 1
Masivní mosazná koule o objemu 0,8 m3 klesá do oceánu do hloubky, kde je hydrostatický tlak o 20 M Pa větší než na povrchu. Jak se změní objem koule? Je známo, že modul stlačitelnosti mosazi je B = 35 000 MPa,
Řešení
1 M Pa = 1 Mega pascal = 1. 10 6 Pa
Kolísání tlaku vzhledem k povrchu je DP = 20 x 10 6 Pa. Použitím rovnice dané pro B máme:
B = -ΔP / (ΔV / Vnebo)
Proto:

ΔV = -5,71,10 -4 x 0,8 m3 = -4,57 x 10-4 m3
Rozdíl v objemu může mít záporné znaménko, pokud je konečný objem menší než počáteční objem, proto tento výsledek souhlasí se všemi předpoklady, které jsme doposud učinili.
Velmi vysoký modul stlačitelnosti naznačuje, že je zapotřebí velké změny tlaku, aby objekt zaznamenal znatelné zmenšení objemu..
-Cvičení vyřešeno 2
Přiložením ucha k železniční trati poznáte, kdy se jedno z těchto vozidel blíží v dálce. Jak dlouho trvá zvuk při cestování po ocelové kolejnici, pokud je vlak vzdálený 1 km?
Data
Hustota oceli = 7,8 x 10 3 kg / m3
Modul stlačitelnosti oceli = 2,0 x 10 jedenáct Pa.
Řešení

Výpočtový modul stlačitelnosti B platí i pro kapaliny, i když je obecně zapotřebí velkého úsilí, aby se dosáhlo znatelného snížení objemu. Kapaliny se však mohou rozpínat nebo smršťovat při zahřívání nebo ochlazování a stejně tak i v případě, že jsou bez tlaku nebo pod tlakem..
Pro vodu za standardních podmínek tlaku a teploty (0 ° C a tlak jedné atmosféry přibližně nebo 100 kPa) je objemový modul 2100 MPa. To znamená asi 21 000násobek atmosférického tlaku.
Z tohoto důvodu jsou ve většině aplikací kapaliny obvykle považovány za nestlačitelné. To lze okamžitě zkontrolovat pomocí numerické aplikace.
-Cvičení vyřešeno 3
Najděte dílčí pokles objemu vody, když je vystavena tlaku 15 MPa.
Řešení

Stlačitelnost v plynech
Plyny, jak je vysvětleno výše, fungují trochu jinak.
Aby věděli, jaký objem mají n moly daného plynu, pokud jsou udržovány v tlaku P a při teplotě T, používá se stavová rovnice. Ve stavové rovnici pro ideální plyn, kde mezimolekulární síly nejsou brány v úvahu, nejjednodušší model uvádí, že:
P.V.ideál = n. R. T.
Kde R je ideální plynová konstanta.
Změny v objemu plynu lze provádět při konstantním tlaku nebo konstantní teplotě. Například udržováním konstantní teploty izotermická stlačitelnost ΚT to je:

Místo symbolu „delta“, který byl použit dříve při definování konceptu pro pevné látky, je pro plyn popisován derivací, v tomto případě částečnou derivací vzhledem k P, udržující T konstantní.
Proto BT modul izotermické stlačitelnosti je:

A adiabatický modul stlačitelnosti B je také důležitý.adiabatický, pro které neexistuje žádný příchozí ani odchozí tok tepla.
Badiabatický = yp
Kde γ je adiabatický koeficient. S tímto koeficientem lze vypočítat rychlost zvuku ve vzduchu:

Pomocí výše uvedené rovnice najděte rychlost zvuku ve vzduchu.
Data
Adiabatický modul stlačitelnosti vzduchu je 1,42 × 105 Pa
Hustota vzduchu je 1 225 kg / m3 (při atmosférickém tlaku a 15 ° C)
Řešení

Namísto práce s modulem stlačitelnosti, jako jednotková změna objemu na jednu změnu tlaku, faktor stlačitelnosti skutečného plynu, odlišný, ale ilustrativní koncept srovnání skutečného plynu s ideálním plynem:
P. PROTInemovitý = Z. R. T.
Kde Z je koeficient stlačitelnosti plynu, který závisí na podmínkách, ve kterých se nachází, přičemž je obecně funkcí tlaku P i teploty T a lze jej vyjádřit jako:
Z = f (P, T)
V případě ideálního plynu Z = 1. U skutečných plynů se hodnota Z téměř vždy zvyšuje s tlakem a klesá s teplotou.
Jak tlak stoupá, plynné molekuly se srazí častěji a odpudivé síly mezi nimi se zvyšují. To může vést ke zvýšení objemu skutečného plynu, přičemž Z> 1.
Naproti tomu při nižších tlacích se molekuly mohou volně pohybovat a převládají atraktivní síly. V takovém případě Z < 1.
Pro jednoduchý případ 1 molu plynu n = 1, pokud jsou zachovány stejné tlakové a teplotní podmínky, vydělením předchozího výrazu rovnicí členem získáme:

PROTInemovitý = Z Videál
-Cvičení vyřešeno 5
Existuje skutečný plyn při 250 ° K a tlaku 15 atm, který má molární objem o 12% menší než ten, který je vypočítán stavovou rovnicí ideálního plynu. Pokud jsou tlak a teplota udržovány konstantní, najděte:
a) Faktor stlačitelnosti.
b) Molární objem skutečného plynu.
c) Jaký typ sil převládá: atraktivní nebo odpudivé?
Řešení
a) Pokud je skutečný objem o 12% menší než ideální, znamená to, že:
PROTInemovitý = 0,88 Videál
Proto pro 1 mol plynu je faktor stlačitelnosti:
Z = 0,88
b) Výběr ideální konstanty plynu s příslušnými jednotkami pro dodaná data:
R = 0,082 L.atm / mol.K
Molární objem se vypočítá řešením a nahrazením hodnot:
c) Převažují atraktivní síly, protože Z je menší než 1.
Reference
- Atkins, P. 2008. Fyzikální chemie. Redakční Médica Panamericana. 10 - 15.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6th. Sál Eda Prentice. 242 - 243 a 314-15
- Mott, R. 2006. Fluid Mechanics. Pearson Education 13-14.
- Rex, A. 2011. Základy fyziky. Pearson Education. 242-243.
- Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vyd. Svazek 1. Redakční reverté. 542.


Zatím žádné komentáře