The tlak nebo tlakové napětí je síla na jednotku plochy, jejímž výsledkem je tlačit, mačkat nebo stlačit předmět, který má tendenci jej zkrátit. Matematicky to je:
E = F / A
Tady A označuje úsilí, F velikost síly a NA oblast, na kterou působí, jednotka v mezinárodním systému SI je newton / mdva nebo pascal (Pa). Tlakový stres je a normální úsilí, protože síla, která ji vytváří, je kolmá na oblast, na kterou působí.
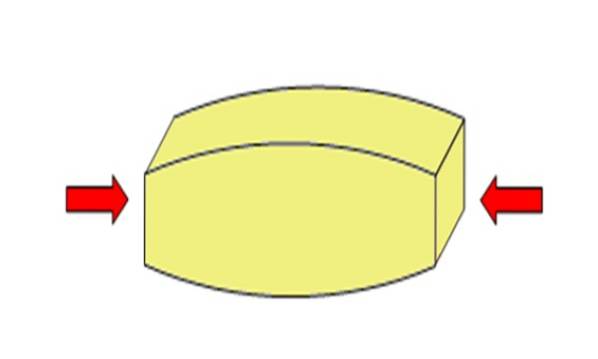
Takové úsilí může předmět stlačit, nebo naopak napnout a natáhnout, jak je aplikováno. V případě tlakového napětí jsou síly aplikovány v opačném směru, aby se dosáhlo účinku stlačení a zkrácení objektu.
Jakmile síly ustanou, mnoho materiálů se vrátí do svých původních rozměrů. Tato vlastnost je známá pod jménem pružnost. Ale když k tomu dojde, deformace elastické jednotky, kterou utrpěl materiál vystavený namáhání, je:
Kmen = (konečná velikost - počáteční velikost) / počáteční velikost
Kmen může být lineární, povrchový nebo objemový, i když kmen je bezjednotkový. Informace, které poskytuje, jsou však velmi důležité, protože není stejné deformovat 10 m dlouhou tyč o 1 cm, deformovat další 1 m dlouhou tyč o 1 cm.
V elastickém materiálu jsou deformace a napětí úměrné a splňují Hookeův zákon:
Úsilí ∝ Deformace jednotky
Rejstřík článků
Napětí v tlaku způsobí, že se částice materiálu přibližují a přibližují, čímž se zmenšuje jejich velikost. V závislosti na směru, ve kterém je úsilí aplikováno, dojde ke zkrácení nebo zmenšení některých jeho rozměrů.
Začněme tím, že předpokládáme tenkou čáru původní délky L, na které je normální napětí velikosti A. Je-li napětí kompresní, dojde u prutu ke zmenšení jeho délky, označené δ. Pokud je to napětí, tyč se prodlouží.
Přirozeně je materiál, ze kterého je prvek vyroben, rozhodující pro jeho schopnost odolávat stresu..
Tyto elastické vlastnosti materiálu jsou zahrnuty do výše uvedené konstanty proporcionality. Je pojmenován modul pružnosti nebo Youngův modul a označuje se jako Y. Každý materiál má modul pružnosti, který je stanoven experimentálně laboratorními testy.
S ohledem na tuto snahu A Vyjadřuje se v matematické formě takto:
Úsilí ∝ Deformace jednotky
Nakonec, aby se tato podmínka stanovila jako rovnice, je nutná konstanta proporcionality, která nahradí symbol proporcionality ∝ a nahradí jej rovností, například takto:
Napětí = Konstanta proporcionality x Jednotkové napětí
E = Y. (δ / L)
Kvocient (δ / L) je kmen, označený jako ε as δ = Konečná délka - počáteční délka. Tímto způsobem úsilí A vypadá jako:
E = Y. ε
Protože deformace je bezrozměrná, jednotky Y jsou stejné jako u A: N / mdva o Pa v systému SI, libry / palcedva nebo psi v britském systému, stejně jako další kombinace síly a plochy, například kg / cmdva.
Hodnoty Y jsou stanoveny experimentálně v laboratoři za kontrolovaných podmínek. Dále modul pružnosti pro materiály široce používané ve stavebnictví a také pro kosti:
stůl 1
| Materiál | Modul pružnosti Y (Pa) x 109 |
|---|---|
| Ocel | 200 |
| Žehlička | 100 |
| Mosaz | 100 |
| Bronz | 90 |
| Hliník | 70 |
| Mramor | padesátka |
| Žula | Čtyři pět |
| Beton | dvacet |
| Kost | patnáct |
| Borové dřevo | 10 |
Tlakové síly působí na různé struktury; Podléhají působení sil, jako je váha každého z prvků, které je tvoří, stejně jako síly od vnějších činitelů: vítr, sníh, další struktury a další..
Je obvyklé, že většina konstrukcí je navržena tak, aby vydržela napětí všeho druhu bez deformace. Proto je třeba vzít v úvahu tlakové napětí, aby se zabránilo ztrátě tvaru součásti nebo předmětu..
Také kosti kostry jsou struktury vystavené různým namáháním. I když jsou kosti vůči nim odolné, při náhodném překročení meze pružnosti vznikají trhliny a zlomeniny.
Stavební sloupy a pilíře musí být vyrobeny tak, aby odolávaly stlačení, jinak mají sklon se uklánět. Toto je známé jako boční ohýbání nebo vzpěr.
Sloupy (viz obrázek 1) jsou prvky, jejichž délka je podstatně větší ve srovnání s jejich průřezovou plochou..
Válcovým prvkem je sloup, pokud je jeho délka stejná nebo větší než desetinásobek průměru průřezu. Pokud však průřez není konstantní, bude použit menší průměr, aby byl prvek klasifikován jako sloup.
Když se lidé posadí na nábytek, jako jsou židle a lavice, nebo přidají nějaké předměty na vrch, pak jsou nohy vystaveny tlakovým tlakům, které mají sklon snižovat jejich výšku..
Nábytek je obvykle vyroben tak, aby dobře odolal hmotnosti a po odstranění se vrátí do svého přirozeného stavu. Pokud je však na křehké židle nebo lavice kladena velká váha, nohy se stlačí a zlomí..
Existuje tyč, která měří původně 12 m na délku a na kterou je vystaveno tlakovému napětí, takže její jednotková deformace je -0 0004. Jaká je nová délka prutu?
Počínaje výše uvedenou rovnicí:
ε = (δ / L) = - 0,0004
Ano LF je konečná délka a Lnebo počáteční délka, protože 5 = LF - Lnebo ty máš:
(L.F - Lnebo) / L.nebo = -0 0004
Proto: LF - Lnebo = -0 0004 x 12 m = -0,0048 m. A nakonec:
LF = (12 - 0,0048) m = 11,9952 m.
Masivní ocelová tyč, válcového tvaru, je 6 m dlouhá a 8 cm v průměru. Pokud je tyč stlačena při zatížení 90 000 kg, najděte:
a) Velikost tlakového napětí v megapascalech (MPa)
b) O kolik se zmenšila délka lišty?
Nejprve najdeme oblast A průřezu tyče, která závisí na jejím průměru D, což má za následek:
A = π. Ddva / 4 = π. (0,08 m)dva / 4 = 5,03 x 10-3 mdva
Síla je okamžitě nalezena, skrz F = m.g = 90 000 kg x 9,8 m / sdva= 882 000 N..
Nakonec se průměrné úsilí vypočítá takto:
E = F / A = 882 000 N / 5,03 x 10-3 mdva = 1,75 x 108 Pa = 175 MPa
Nyní se používá rovnice pro napětí s vědomím, že materiál má elastickou odezvu:
E = Y. (δ / L)
Youngův modul oceli je uveden v tabulce 1:
5 = E.L / Y = 6 m x 1,75 x 108 Pa / 200 x 10 9 Pa = 5,25 x 10 -3 m = 5,25 mm.
Zatím žádné komentáře