
Zachování principu lineární hybnosti, příklady, cvičení.
The zachování lineární hybnosti tělesa stanoví, že součin jeho hmotnosti a jeho vektoru rychlosti je konstantní veličina, když je těleso bez interakce s jinými tělesy a s rychlostí měřenou vzhledem k pevnému nebo nezrychlenému referenčnímu rámci.
Pokud máte několik těl, která interagují pouze navzájem, ale ne s vnějším prostředím, pak lineární hybnost soupravy také časem zůstává konstantní.

Lineární hybnost, hybnost nebo jednoduše hybnost, je označen písmenem p y je vektorová veličina:
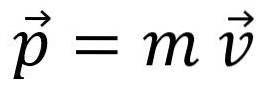
Hybnost není stejná jako rychlost, i když vztah je zřejmý: například nákladní automobil jedoucí rychlostí 20 km / h má větší hybnost než kolo pohybující se stejnou rychlostí.
Aby se lineární hybnost tělesa mohla změnit, musí na něj působit čistá vnější síla, jinak zůstane konstantní. Také lineární moment P systému tvořeného n-těl je vektorový součet jednotlivých momentů:
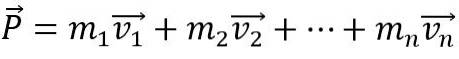
Rejstřík článků
- 1 Princip zachování lineární hybnosti
- 2 Příklady
- 2.1 Příklad 1
- 2.2 Příklad 2
- 2.3 Příklad 3
- 3 Aplikace
- 3.1 Loď ve vesmíru
- 3.2 Každodenní život
- 4 cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Princip zachování lineární hybnosti
V těle bez síly (nebo v těle, ve kterém se všechny síly na něj ruší) se stává, že lineární moment zůstane konstantní.
Totéž se děje v systému tvořeném několika tělesy, která interagují pouze navzájem, ale nikoli s vnějším prostředím: celková lineární hybnost systému zůstává během vývoje pohybu celku neměnná..
Tento princip zachování je uveden následovně:
Celková hybnost sady n-těles, která interagují pouze navzájem, ale ne s vnějším prostředím, je neměnná veličina v čase.
A matematicky je to vyjádřeno takto:
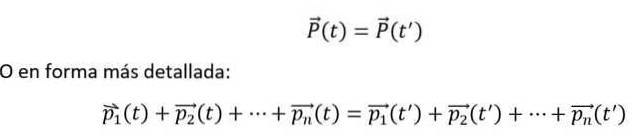
Výše uvedené rovnosti jsou splněny, pouze a pouze v případě, že n-těla interagují navzájem, ale ne s vnějším prostředím. Kromě toho musí být vždy měřeny jednotlivé momenty vzhledem k setrvačnému referenčnímu rámci..
Příklady
Příklad 1

Dva astronauti ve vesmíru se drží za ruce a jsou drženi ve pevné poloze vzhledem ke kosmické lodi. Pokud se však navzájem tlačí, začnou se při pohledu z lodi oddělovat opačným směrem..
V tomto případě, protože interakce mezi astronauty probíhá pouze mezi nimi prostřednictvím kontaktní síly jejich rukou, je celková hybnost po zatlačení stále počáteční hodnotou s ohledem na kosmickou loď. To znamená, že celková hybnost 0.
Hybnost každého astronauta se však změnila. Zpočátku měl každý z nich 0 lineárních momentů vzhledem k lodi, ale poté, co byl tlačen, jeden vystupuje v jednom směru a druhý v opačném směru, s nenulovými lineárními momenty stejné velikosti a opačnými směry..
Když se tedy jednotlivé momenty sčítají vektorově, získá se jako výsledek počáteční celková hybnost, která je nula.
Na druhou stranu zachování množství hybnosti naznačuje, že astronaut s nejnižší hmotností je ten, který se pohybuje rychleji s ohledem na kosmickou loď. Ale výsledek vynásobení jeho hmotnosti jeho rychlostí se rovná produktu získanému vynásobením hmotnosti druhého rychlostí druhého.
Příklad 2
Štěně je na plovoucí plošině v klidném jezeře a jeho majitel ho sleduje z doku. Na začátku je plošina i štěně v klidu, ale když se štěně chce přiblížit k majiteli, plošina se vzdaluje od doku.
Vysvětlení tohoto pozorování je právě v principu zachování množství lineární hybnosti. Systém se skládá ze štěněte a platformy.
Štěně může chodit po plošině díky třecí síle mezi nohama a povrchem, v tomto případě je třecí síla vnitřní silou interakce mezi ní a plošinou.
Celá je izolovaným systémem, protože plošina se může pohybovat vodorovně nad jezerem bez jakéhokoli odporu proti pohybu. Na druhou stranu ve svislém směru jsou všechny síly vyvážené a kompenzované a celek se v tomto směru nepohybuje..
Proto jsou v této situaci splněny všechny hypotézy, takže platí princip zachování lineární hybnosti.
Příklad 3

Eskymák je uvězněn uprostřed zamrzlého jezera, led je tak hladký, že bez ohledu na to, jak moc se snaží, Eskimák uklouzne a vždy zůstane na stejném místě.
Jediným možným způsobem, jak se Eskimák může dostat z jezera, je házet opačným směrem, kterým chce pohnout těžkým předmětem, který nosí v batohu (za předpokladu, že ho nese)..
Aplikace
Loď ve vesmíru

Zachování lineární hybnosti se aplikuje na pohon rakety do vesmíru, kde nepůsobí žádné vnější síly. V tomto případě je impuls lodi dosažen vypuzováním plynů vysokou rychlostí, takže raketa se může pohybovat v opačném směru, do kterého byly vyhozeny..
Pokud je loď původně v klidu, dojde při spalování a vypuzení paliva k síle vypuzení proti samotné lodi. Je to vnitřní síla mezi plyny a lodí. Neexistují žádné vnější síly, a proto platí zachování lineární hybnosti.
Vzhledem k tomu, že lineární hybnost plynů je stejná a opačná než u lodi, dokáže vyjít z klidu a pokračováním ve vypuzování plynů zvyšuje jeho množství pohybu, a tím i rychlost.
Každodenní život

Dalším případem aplikace zachování lineární hybnosti v každodenním životě je zatloukání hřebíku do dřeva s využitím množství pohybu nebo hybnosti kladiva..
Lze tvrdit, že v tomto případě zásada neplatí, protože existuje vnější síla: odpor, který dřevo hřebu nabízí..
V okamžiku kontaktu je však síla, kterou kladivo působí na hřebík, vnitřní silou (mezi systémem, kterým je hřebík a kladivem), mnohem větší než odpor, kterému dřevo odporuje, a proto je tento odpor zanedbatelný.
Celá hybnost kladiva, která je díky své velké hmotnosti a rychlosti poměrně velká, se ihned po srážce přenáší na hřebík. Všimněte si, že se přenáší celý okamžik, ale ne veškerá kinetická energie kladiva, protože část se transformuje na tepelnou energii v hřebíku a v kladivu, která po nárazu zvýší jejich teplotu.
Výcvik
Cvičení 1
Astronauti Andrew a Berenice jsou před vesmírnou stanicí a drží obě ruce v klidu vzhledem ke stanici. Jsou poháněni tlačením rukou jednoho proti druhému a jsou uvolněni. Pokud se Andrew, 70 kg hmoty, pohybuje rychlostí 1 m / s vzhledem k stanici, jaká je rychlost Berenice se 49 kg hmotnosti?
Řešení
V tomto případě platí jasně hypotézy zachování lineární hybnosti, protože ve vesmíru neexistují žádné vnější síly. Síla, kterou oba astronauti tlačí na své ruce, je vnitřní silou.
Předpokládejme, že Andrewova mše je M.na a to Berenice M.b. Podobně jsou rychlosti obou po impulsu PROTIna pro Andrewa a PROTIb pro Berenice. Pak platí zachování lineární hybnosti takto:
Mna∙0 + Mb∙0 = M.na∙PROTIna+ Mb∙PROTIb
Řešení rychlosti Berenice máme:
PROTIb = - (M.na / Mb) ∙ PROTIna
Umístění číselných hodnot:
PROTIb = - (70/49) ∙ (1 m / s) nebo = -1,43 m / s nebo
To znamená, že Berenice se pohybuje rychlostí 1,43 m / s opačným směrem než Andrew.
Cvičení 2

Štěně o hmotnosti 5 kg odpočívá na 15 kg plošině, která plave, také v klidu, na klidném jezeře. Pokud štěně začne na plošině chodit rychlostí 0,5 m / s vzhledem k ní. Jak rychle bude mít štěně a plošina vůči pozorovateli připevněnému k zemi??
Řešení
Inerciální referenční systém bude považován za dokovací stanici, kde je majitel štěněte. Zpočátku je štěně i plovoucí plošina v klidu vzhledem k doku..
Když se štěně rozhodne rychle kráčet směrem k majiteli v ' relativně k plošině, pak se plošina pohybuje od mola rychlostí +PROTI. Rychlost štěněte vzhledem k pružině se získá pomocí vektorového součtu jeho rychlosti vzhledem k plošině plus rychlosti plošiny a označíme ji:
proti = -proti'' + PROTI
Vzhledem k tomu, že odpor vody vůči pohybu plošiny je díky své nízké rychlosti prakticky nulový, lze konstatovat, že systém tvořený štěně + platforma je izolovaný systém a platí princip zachování lineární hybnosti:
0 = m ∙ v + M ∙ V
Pamatujeme, že v = v '+ V máme:
0 = -m ∙ v '+ m ∙ v + M ∙ V
To znamená: m ∙ v '= (m + M) ∙ V
Proto V = [m / (m + M)] v 'a v = - (M / m) V = - [M / (m + M)] v'
Dosazením numerických hodnot máme:
V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s
To je rychlost, jakou se platforma pohybuje od doku.
V = - (15/20) ∙ 0,5 m / s = -0,375 m / s
A to je rychlost, s jakou se štěně přibližuje k doku.
Reference
- Duke University. Systémy částic. Obnoveno z: webhome.phy.duke.edu.
- Rex, A. 2011. Základy fyziky. Pearson.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vyd. 1. díl Pearson.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.
- .


Welcome to the world of adult Dating loveawake.ru