
Absolutní konstantní koncept a vysvětlení, příklady
The absolutní konstanty jsou ty konstanty, které si vždy během procesu výpočtu udržují svoji hodnotu. Všechny absolutní konstanty jsou číselné hodnoty a v některých případech jsou reprezentovány písmeny, která tvoří řeckou abecedu.
Koncept konstantní velikosti odkazuje na ten, jehož hodnota zůstává pevná; To znamená, že jeho hodnota se nemění a vždy zůstává stejná. Tato hodnota se nemění, dokud trvá situace nebo proces, pro který se tato velikost používá.

Rejstřík článků
- 1 Koncept a vysvětlení
- 2 Aplikace a příklady
- 2.1 Aplikace v matematice
- 2.2 Aplikace ve fyzice
- 2.3 Aplikace v chemii
- 2.4 Aplikace v programování
- 3 Odkazy
Koncept a vysvětlení
Konstanty jsou absolutní, protože jejich hodnota se při provádění postupu výpočtu nikdy nemění. Tito jsou také známí jako číselné konstanty, protože, jak naznačuje jejich název, jsou to hodnoty představované čísly a v některých případech písmeny, například:
- V rovnici: y = 4x + 1 jsou absolutní konstanty 4 a 1.
Existuje mnoho oblastí, kde jsou implementovány absolutní konstanty; například v oblastech jako fyzika, chemie a matematika je jejich použití velmi důležité, protože pomáhají řešit nekonečné množství problémů.
Existuje mnoho hodnot konstant, které slouží jako reference v různých alternativách řešení cvičení; Absolutní konstanty, jako je plocha a objem, jsou jednou z nejpoužívanějších v oborech, jako je strojírenství.
Aplikace a příklady
Aplikace v matematice
V této oblasti existuje několik čísel, která představují absolutní konstanty, které historicky pomohly při řešení mnoha problémů, které pomohly při vývoji lidstva..
Pi (π)
Jednou z velmi důležitých konstant je pi (π), která byla studována od starověku (1800 př. N. L.).
O mnoho století později to byl Archimedes, kdo určil jeho hodnotu, což je iracionální číslo, které odráží vztah mezi délkou obvodu a jeho průměrem..
Toto bylo vypočítáno na základě různých aproximací, jeho číselná hodnota je: 3,1415926535… a skládá se z přibližně 5 000 * 109 desetinná místa.
Z konstanty π bylo možné v geometrii odvodit plochu a objem rotačních kónických řezů a těles, jako například kruh, válec, kužel, koule atd. Používá se také k vyjádření rovnic v radiánech.
Zlaté číslo (φ)
Další velmi důležitá konstanta použitá nebo nalezená v různých oblastech je zlaté číslo (φ), nazývané také zlaté číslo nebo zlatá střední cesta. Je to vztah nebo poměr mezi dvěma segmenty úsečky, vyjádřený rovnicí:
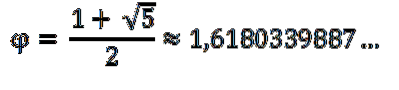
Byl objeven ve starověku a studován Euklidem. Tento vztah je zastoupen nejen v geometrických obrazcích, jako jsou pětiúhelníky, ale také v přírodě, například ve skořápce šneka, v mušlích, v semenech slunečnice a v listech. Může se také nacházet v lidském těle.
Tento vztah je znám jako božská proporce, protože připisuje věcem estetický charakter. Z tohoto důvodu se používá v architektonickém designu a různí umělci, jako je Leonardo Da Vinci, jej implementovali do svých děl..
Ostatní konstanty
Další absolutní konstanty, které jsou široce uznávány a mají stejný význam, jsou:
- Pythagorova konstanta: √2 = 1,41421…
- Eulerova konstanta: γ = 0,57721…
- Přirozený logaritmus: e = 2,71828 ...
Aplikace ve fyzice
Ve fyzice je absolutní konstanta ta velikost, jejíž hodnota vyjádřená v soustavě jednotek zůstává ve fyzikálních procesech v průběhu času nezměněna..
Jsou známé jako univerzální konstanty, protože byly zásadní pro studium různých procesů od nejjednodušších po nejsložitější jevy. Mezi nejznámější patří:
Konstanta rychlosti světla ve vakuu (c)
Jeho hodnota je přibližně 299 792 458 m* s-1. Používá se k definování jednotky délky, kterou světlo prochází za rok, a z toho se rodí měření délkového metru, což je pro měřicí systémy zásadní.
Konstanta univerzální gravitace (G)
To určuje intenzitu gravitační síly mezi tělesy. Je součástí studií Newtona a Einsteina a jeho přibližná hodnota je 6,6742 (10) * 10-jedenáct N*mdva/ kgdva.
Konstanta permitivity ve vakuu (ε0)
Tato konstanta se rovná 8,854187817 ... * 10-12 F.*m-1.
Konstanta magnetické permeability ve vakuu (μ0)
Což se rovná 1,25566370 * 10-6 N.NA-dva.
Aplikace v chemii
V chemii, stejně jako v jiných oblastech, je absolutní konstanta ta data, princip nebo skutečnost, která nepodléhá změnám nebo variacím; odkazuje na konstanty těla nebo na sadu znaků, které nám umožňují odlišit jeden chemický druh od druhého, například molekulární a atomovou hmotnost každého prvku.
Mezi hlavní absolutní chemické konstanty patří:
Avogadro číslo (NNA)
Je to jedna z nejdůležitějších konstant. S tímto je možné počítat mikroskopické částice k určení hmotnosti atomu; vědec Amedeo Avogadro tak stanovil, že 1 mol = 6,022045 * 102. 3 krtek-1.
Hmotnost elektronu (ma)
Rovná se 9, 10938 *10-31
Protonová hmota (mp)
Tato konstanta se rovná 1,67262 *10-27
Neutronová hmota (mn)
Rovná se 1,67492* 10-27
Radio Bohr (a0)
Odpovídá 5,29177*10-11
Poloměr elektronů (ra)
Což se rovná 2, 81794*10-15
Konstanta plynu (R)
Konstanta, která se rovná 8,31451 (mdva*kg) / (K.* krtek* sdva)
Aplikace v programování
Absolutní konstanta se používá také v oblasti počítačového programování, ve které je definována jako hodnota, kterou nelze změnit při provádění programu; to je v tomto případě pevná délka, která je vyhrazena z paměti počítače.
V různých programovacích jazycích jsou konstanty vyjádřeny pomocí příkazů.
Příklad
- V jazyce C jsou absolutní konstanty deklarovány příkazem „#define“. Tímto způsobem bude konstanta udržovat stejnou hodnotu během provádění programu..
Například pro označení hodnoty Pi (π) = 3,14159 napíšeme:
#zahrnout
#define PI 3.1415926
int main ()
printf ("Pi má hodnotu% f", PI);
návrat 0;
- V jazycích C ++ i Pascal jsou konstanty přikázány slovem „const“.
Reference
- Anfonnsi, A. (1977). Diferenciální a integrální počet.
- Arias Cabezas, J. M., & Maza Sáez, I. d. (2008). Aritmetika a algebra.
- Harris, D. C. (2007). Kvantitativní chemická analýza.
- Meyer, M. A. (1949). Analytická geometrie. Redakční program.
- Nahin, P. J. (1998). Imaginární příběh. Princeton University Press;.
- Rees, P. K. (1986). Algebra. Reverte.



Zatím žádné komentáře