The Boltzmannova konstanta je hodnota, která souvisí s průměrnou kinetickou energií termodynamického systému nebo objektu s jeho absolutní teplotou. I když jsou často zmateni, teplota a energie nejsou stejný koncept.
Teplota je měřítkem energie, ale nikoli energií samotnou. S Boltzmannovou konstantou jsou navzájem propojeny následujícím způsobem:
AC = (3/2) kB T
Tato rovnice je platná pro monatomickou ideální molekulu plynu o hmotnosti m, kde AC je jeho kinetická energie daná v Joulech, kB je Boltzmannova konstanta a T je absolutní teplota v Kelvinech.
Tímto způsobem, jak se zvyšuje teplota, se zvyšuje průměrná kinetická energie na molekulu látky, jak se očekává. A opak se stane, když teplota poklesne a bude schopna dosáhnout bodu, kdy pokud veškerý pohyb ustane, je dosaženo nejnižší možné teploty nebo absolutní nuly..
Když mluvíme o průměrné kinetické energii, je třeba si uvědomit, že kinetická energie je spojena s pohybem. A částice se mohou pohybovat mnoha způsoby, například pohybem, otáčením nebo vibracemi. Samozřejmě, ne všichni to udělají stejným způsobem, a protože jsou nepočitatelní, pak se pro charakterizaci systému použije průměr..
Některé energetické stavy jsou pravděpodobnější než jiné. Tento koncept má v termodynamice zásadní význam. Energie uvažovaná ve výše uvedené rovnici je translační kinetická energie. Pravděpodobnost stavů a jejich vztah s Boltzmannovou konstantou budou probrány o něco později..
V roce 2018 byl nově definován Kelvin a s ním Boltzmannova konstanta, která v mezinárodním systému činí přibližně 1,380649 x 10-2. 3 J. K.-1. Mnohem větší přesnosti lze dosáhnout Boltzmannovy konstanty, která byla stanovena v mnoha laboratořích po celém světě, různými metodami..
Rejstřík článků
Slavná konstanta vděčí za své jméno vídeňskému fyzikovi Ludwigovi Boltzmannovi (1844-1906), který zasvětil svůj život vědce studiu statistického chování systémů s mnoha částicemi z pohledu newtonovské mechaniky..
Ačkoli dnes je existence atomu všeobecně přijímána, v devatenáctém století byla v plné debatě víra o tom, zda atom skutečně existoval, nebo byl rafinovaností, s níž bylo vysvětleno mnoho fyzikálních jevů..
Boltzmann byl horlivým obhájcem existence atomu a ve své době čelil tvrdé práci svého kolegu od mnoha kolegů, kteří se domnívali, že obsahuje neřešitelné paradoxy..
Uvedl, že pozorovatelné jevy na makroskopické úrovni lze vysvětlit statistickými vlastnostmi základních částic, jako jsou atomy a molekuly..
Možná, že tato kritika byla způsobena hlubokou epizodou deprese, která ho vedla k tomu, aby si vzal život na začátku září 1906, kdy měl ještě co dělat, protože byl považován za jednoho z velkých teoretických fyziků své doby a tam byl zbývá jen velmi málo, aby ostatní vědci přispěli k potvrzení pravdivosti jejich teorií.
Nedlouho po jeho smrti se objevily nové objevy o povaze atomu a jeho složkách, které prokázaly Boltzmannovu pravdu..
Boltzmannova konstanta kB bylo představeno, jak je dnes známé, nějakou dobu po dílech rakouského fyzika. Byl to Max Planck, podle svého zákona o vyzařování černého těla, dílo, které představil v roce 1901, a v té době mu dal hodnotu 1,34 x 10-23 J / K..
Kolem roku 1933 byla k Boltzmannovu náhrobku ve Vídni přidána pamětní deska s definicí entropie zahrnující slavnou konstantu jako posmrtná pocta: S = kB log W, rovnice, o které bude pojednáno později.
Dnes je Boltzmannova konstanta nepostradatelná při aplikaci zákonů termodynamiky, statistické mechaniky a teorie informace, v nichž byl tento smutně končící fyzik průkopníkem..
Plyny lze popsat makroskopicky a také mikroskopicky. Pro první popis existují pojmy jako hustota, teplota a tlak.
Mělo by se však pamatovat na to, že plyn se skládá z mnoha částic, které mají globální tendenci k určitému chování. Právě tento trend se měří makroskopicky. Jedním ze způsobů, jak určit Boltzmannovu konstantu, je známá rovnice ideálního plynu:
p.V = n. R. T.
Tady p je tlak plynu, PROTI je jeho objem, n je počet přítomných krtků, R je plynová konstanta a T je teplota. V jednom molu ideálního plynu je mezi výrobkem splněn následující vztah p.V, a translační kinetická energie K. celá sada je:
p.V = (2/3). K.
Kinetická energie je tedy:
K = (3/2) n.R.T.
Vydělením celkovým počtem přítomných molekul, které se bude jmenovat N, se získá průměrná kinetická energie jedné částice:
AC = K / N
AC= (3 / 2N) n.R.T.
V jednom molu je Avogadroův počet částic NNA, a proto je celkový počet částic N = nNA, zbývající:
AC = (3 / 2nNNA) n.R.T.
Přesně kvocient R / NNA je Boltzmannova konstanta, čímž se ukazuje, že průměrná translační kinetická energie částice závisí pouze na absolutní teplotě T a nikoli na jiných veličinách, jako je tlak, objem nebo dokonce typ molekuly:
AC = (3/2) kB. T
Plyn má danou teplotu, ale tato teplota může odpovídat různým stavům vnitřní energie. Jak si tento rozdíl vizualizovat?
Zvažte současné losování 4 mincí a způsoby, jak mohou padnout:
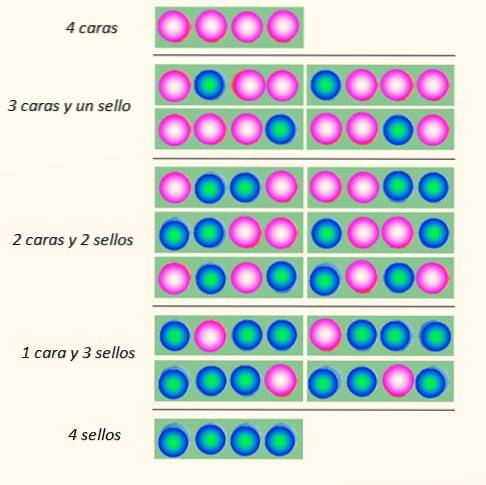
Sada mincí může předpokládat celkem 5 stavů, které jsou brány v úvahu makroskopické, popsáno na obrázku. Čí z těchto států by čtenář řekl, že je nejpravděpodobnější?
Odpovědí by měl být stav 2 hlav a 2 ocasů, protože máte celkem 6 možností, z 16 ilustrovaných na obrázku. A 24 = 16. Jsou ekvivalentní stavům mikroskopický.
Co když se hodí 20 mincí místo 4? Byly by celkem 2dvacet možnosti nebo „mikroskopické stavy“. Je to mnohem větší počet a obtížnější manipulace. Pro usnadnění manipulace s velkými čísly jsou logaritmy velmi vhodné.
Nyní se zdá evidentní, že stát s největší poruchou je nejpravděpodobnější. Uspořádanější stavy jako 4 hlavy nebo 4 pečeti jsou o něco méně pravděpodobné.
Entropie makroskopického stavu S je definována jako:
S = kB ve w
Kde w je počet možných mikroskopických stavů systému a kB je Boltzmannova konstanta. Co ve w je bezrozměrný, entropie má stejné jednotky jako kB: Joule / K..
Toto je slavná rovnice na Boltzmannově náhrobku ve Vídni. Více než entropie je však relevantní její změna:
ΔS = kB ve wdva - kB ve w1 = kB ln (wdva/ t1)
Hodnota Boltzmannovy konstanty se získává experimentálně s extrémní přesností pomocí měření založených na akustická termometrie, které se provádějí pomocí vlastnosti, která stanoví závislost rychlosti zvuku v plynu na jeho teplotě.
Rychlost zvuku v plynu je dána vztahem:
Badiabatický = yp
A ρ je hustota plynu. Pro výše uvedenou rovnici, p je tlak dotyčného plynu a y je adiabatický koeficient, jehož hodnota pro daný plyn je uvedena v tabulkách.
Metrologické ústavy také experimentují s jinými způsoby měření konstanty, jako je např Johnsonova hluková termometrie, který využívá teplotní výkyvy, které se vyskytují náhodně v materiálech, zejména vodičích.
Nalézt:
a) Průměrná translační kinetická energie AC který má ideální molekulu plynu při 25 ° C
b) Translační kinetická energie K. molekul v 1 molu tohoto plynu
c) Průměrná rychlost molekuly kyslíku při 25 ° C
mkyslík = 16 x 10 -3 kg / mol
na) AC = (3/2) k T = 1,5 x 1,380649 x 10-2. 3J. K.-1 x 298 K = 6,2 x 10-dvacet jedna J
b) K = (3/2) n.R.T = 5 x 1 mol x 8,314 J / mol. K x 298 K = 3716 J
C) AC = ½ mvdva, vezmeme-li v úvahu, že molekula kyslíku je rozsivková a molární hmotnost musí být vynásobena 2, budeme mít:
Najděte změnu entropie, když 1 mol plynu zaujímá objem 0,5 m3 expanduje a zabírá 1 m3.
ΔS = kB ln (wdva/ t1)
wdva= 2Nw1 (Byly 24 mikroskopické stavy pro losování 4 mincí, pamatujete?)
Kde N je počet částic přítomných v 0,5 mol plynu 0,5 x NNA:
ΔS = kB ln (2N w1/ t1) = kB ln 2N= kB 0,5NNA ln 2 = 2,88 J / K
Zatím žádné komentáře