Jaké jsou části karteziánské roviny?

The části karteziánské roviny Skládají se ze dvou reálných linií, kolmých, které rozdělují kartézskou rovinu na čtyři oblasti. Každá z těchto oblastí se nazývá kvadranty a prvky karteziánské roviny se nazývají body. Rovina je společně s osami souřadnic volána Kartézské letadlo na počest francouzského filozofa Reného Descarta, který vynalezl analytickou geometrii.

Tyto dvě čáry (nebo souřadnicové osy) jsou kolmé, protože mezi nimi tvoří úhel 90 ° a protínají se ve společném bodě (počátku). Jedna z čar je vodorovná, nazývá se počátek x (nebo úsečka) a druhá čára je svislá, nazývá se počátek y (nebo souřadnice).

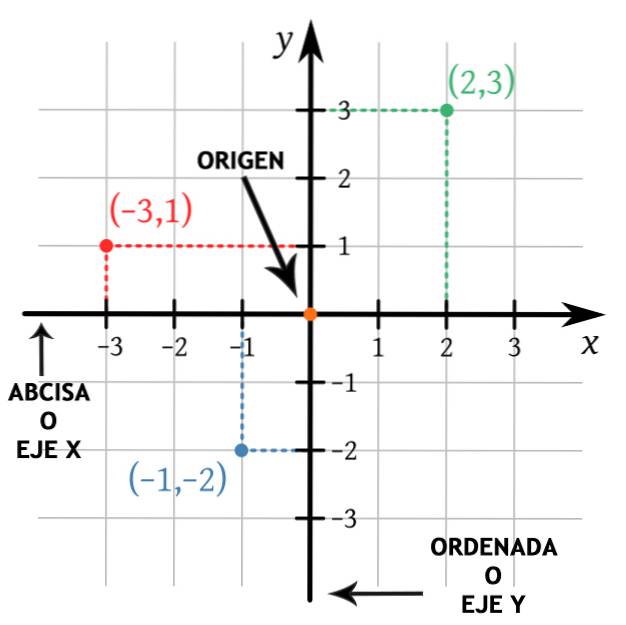
Kladná polovina osy X je napravo od počátku a kladná polovina osy Y je od počátku nahoru. To umožňuje rozlišit čtyři kvadranty karteziánské roviny, což je velmi užitečné při vykreslování bodů v rovině..

Body karteziánské roviny

V každém okamžiku P rovině lze přiřadit dvojici reálných čísel, což jsou její karteziánské souřadnice.

Pokud prochází vodorovná čára a svislá čára P, a tyto protínají osy X a osu Y v bodech na Y b respektive pak souřadnice P Oni jsou (na,b). To se nazývá (na,b) objednaný pár a pořadí, ve kterém jsou čísla zapsána, je důležité.

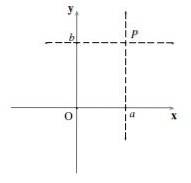
První číslo, na, je souřadnice v „x“ (nebo úsečce) a druhé číslo, b, je souřadnice y (nebo souřadnice). Používá se notace P = (na,b).

Ze způsobu, jakým byla karteziánská rovina konstruována, je zřejmé, že počátek odpovídá souřadnicím 0 na ose „x“ a 0 na ose „y“, tj., NEBO= (0,0).

Kvadranty karteziánské roviny

Jak je vidět na předchozích obrázcích, souřadnicové osy generují čtyři různé oblasti, které jsou kvadranty karteziánské roviny, které jsou označeny písmeny I, II, III Y IV a ty se od sebe liší znakem, který vlastní body, které jsou v každém z nich.

Kvadrant Já

Body kvadrantu Já jsou ty, které mají obě souřadnice s kladným znaménkem, to znamená, že jejich souřadnice x a souřadnice y jsou kladné.

Například bod P = (2,8). Abychom to vytvořili jako graf, bod 2 je umístěn na ose „x“ a bod 8 na ose „y“, potom jsou nakresleny svislé a vodorovné čáry a tam, kde se protínají, je bod. P.

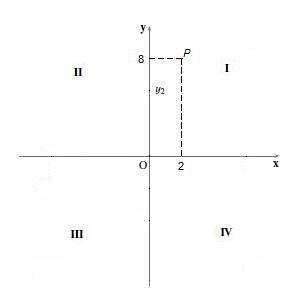
Kvadrant II

Body kvadrantu II mají zápornou souřadnici „x“ a kladnou souřadnici „y“. Například bod Q = (- 4,5). Je graficky znázorněn tak, jako v předchozím případě.

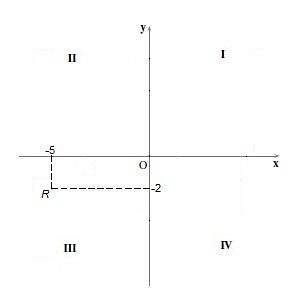
Kvadrant III

V tomto kvadrantu je znaménko obou souřadnic záporné, to znamená, že souřadnice „x“ a souřadnice „y“ jsou záporné. Například bod R = (- 5, -2).

Kvadrant IV

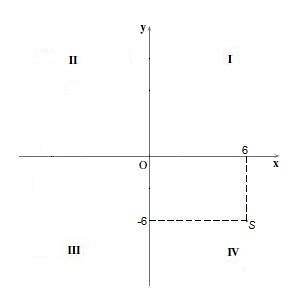
V kvadrantu IV body mají kladnou souřadnici "x" a zápornou souřadnici "y". Například bod S = (6, -6).

Reference

1. Fleming, W., & Varberg, D. (1991). Algebra a trigonometrie s analytickou geometrií. Pearson Education.
2. Larson, R. (2010). Precalculus (8 ed.). Cengage Learning.
3. Leal, J. M. a Viloria, N. G. (2005). Rovinová analytická geometrie. Mérida - Venezuela: Redakční Venezolana C. A.
4. Oteyza, E. (2005). Analytická geometrie (Druhé vydání.). (G. T. Mendoza, ed.) Pearson Education.
5. Oteyza, E. d., Osnaya, E. L., Garciadiego, C. H., Hoyo, A. M., & Flores, A. R. (2001). Analytická geometrie a trigonometrie (První vydání). Pearson Education.
6. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Výpočet (Deváté vydání.). Hala Prentice.
7. Scott, C. A. (2009). Kartézská rovinná geometrie, část: Analytical Conics (1907) (dotisk ed.). Zdroj blesku.