
Derivace kotangensového výpočtu, důkaz, cvičení
The derivace kotangensu se rovná opaku čtverce kosekans "-Cscdva“. Tento vzorec se řídí zákony derivace podle definice a diferenciace trigonometrických funkcí. Označuje se takto:
d (ctg u) = -cscdva nebo du
Kde „du“ symbolizuje výraz odvozený z funkce argumentu s ohledem na nezávislou proměnnou.

Rejstřík článků
- 1 Jak se počítá?
- 2 Charakteristika kotangensové funkce
- 2.1 Vertikální asymptoty
- 2.2 Doména
- 2.3 Rozsah
- 2.4 Frekvence
- 2.5 Chování
- 3 Ukázka
- 3.1 Trigonometrický diferenciální důkaz
- 3.2 Důkaz podle definice derivátu
- 4 Vyřešená cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Jak se to počítá?
Postup vývoje těchto derivátů je poměrně jednoduchý. Jediné, co musíte udělat, je správně identifikovat argument a typ funkce, kterou představuje..
Například výraz Ctg (f / g) má ve svém argumentu rozdělení. To bude vyžadovat rozlišení, pokud jde o U / V, po vytvoření derivace kotangensu.
Kotangens je převrácená hodnota tangensu. Algebraicky to znamená, že:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Je nesprávné tvrdit, že kotangensová funkce je „inverzní“ tečny. Důvodem je, že inverzní tangensová funkce je podle definice oblouková tangenta.
(Tg-1 x) = arctg x
Podle Pythagorovy trigonometrie je kotangens zapojen do následujících částí:
Ctg x = (cos x) / (sin x)
Ctgdva x + 1 = Cscdva X
Podle analytické trigonometrie reaguje na následující identity:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgdva a) / (2tg a)
Vlastnosti kotangensové funkce
Je nutné analyzovat různé charakteristiky funkce f (x) = ctg x, abychom definovali aspekty nutné ke studiu její diferencovatelnosti a aplikace.
Vertikální asymptoty
Funkce kotangens není definována na hodnotách, které činí výraz „Senx“ nula. Díky ekvivalentu Ctg x = (cos x) / (sin x) bude mít neurčitost ve všech „nπ“, přičemž n patří k celým číslům.
To znamená, že v každé z těchto hodnot x = nπ bude vertikální asymptota. Jak se přiblížíte zleva, hodnota kotangensu se rychle sníží a jak se přiblížíte zprava, funkce se bude zvyšovat na neurčito.
Doména
Doménu kotangensové funkce vyjadřuje množina x ∈ R / x ≠ nπ, n ∈ Z. Toto se čte jako „x patřící do množiny reálných čísel tak, že x se liší od nπ, přičemž n patří do množiny celých čísel“.
Hodnost
Rozsah funkce kotangens je od minus do plus nekonečna. Lze tedy dojít k závěru, že jeho rozsah je množina reálných čísel R.
Frekvence
Kotangensová funkce je periodická a její perioda se rovná π. Tímto způsobem je splněna rovnost Ctg x = Ctg (x + nπ), kde n patří Z.
Chování
Je to zvláštní funkce, protože Ctg (-x) = - Ctg x. Tímto způsobem je známo, že funkce představuje symetrii s ohledem na počátek souřadnic. Představuje také pokles v každém intervalu umístěném mezi 2 po sobě následujícími vertikálními asymptoty.
Nemá maximální ani minimální hodnoty, protože jeho aproximace vertikálních asymptot představuje chování, kde se funkce zvyšuje nebo snižuje na neurčito.
Nuly nebo kořeny kotangensové funkce se nacházejí na lichých násobcích π / 2. To znamená, že Ctg x = 0 platí pro hodnoty ve tvaru x = nπ / 2 s n lichým celým číslem.
Demonstrace
Existují 2 způsoby, jak dokázat derivaci kotangensové funkce.
Trigonometrický diferenciální důkaz
Je prokázána derivace kotangensové funkce od jejího ekvivalentu v sinusech a kosinech.
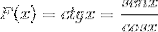
Považuje se to za derivaci rozdělení funkcí
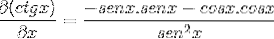
Po odvození jsou faktory seskupeny a cílem je emulovat Pythagorovu identitu
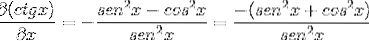
Nahrazením identit a uplatněním vzájemnosti se získá výraz
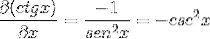
Důkaz podle definice derivátu
Následující výraz odpovídá derivaci podle definice. Kde se vzdálenost mezi 2 body funkce blíží nule.
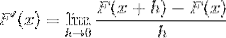
Nahrazení kotangensu máme:
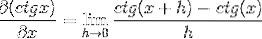
Identity se používají pro součet argumentů a vzájemnosti
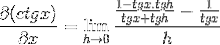
Zlomek čitatele se tradičně ovládá
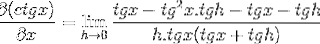
Eliminace opačných prvků a přijetí společného faktoru získáme
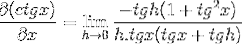
Uplatňování Pythagorovy identity a vzájemnosti musíme
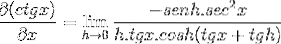
Prvky vyhodnocené v x jsou konstantní vzhledem k limitu, proto mohou opustit argument tohoto. Poté se použijí vlastnosti trigonometrických limitů.
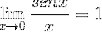
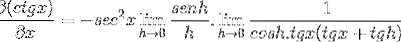
Limit je vyhodnocen
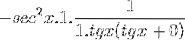
Potom se započítává, dokud není dosaženo požadované hodnoty
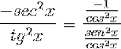
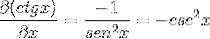
Derivace kotangensu je tak demonstrována jako opak čtverce kosekans.
Vyřešená cvičení
Cvičení 1
Na základě funkce f (x) definujte výraz f '(x)
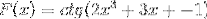
Odpovídající odvození se použije s ohledem na pravidlo řetězu
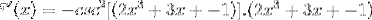
Odvození argumentu
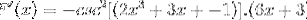
Někdy je nutné k přizpůsobení řešení použít reciproční nebo trigonometrické identity.
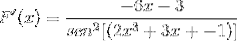
Cvičení 2
Definujte diferenciální výraz odpovídající F (x)
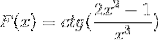
Podle derivačního vzorce a respektování pravidla řetězu
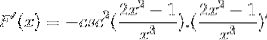
Argument je odvozen, zatímco zbytek zůstává stejný
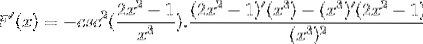
Odvození všech prvků
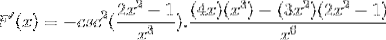
Tradiční provozování produktů stejné základny
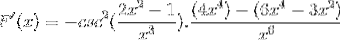
Přidají se stejné prvky a extrahuje se společný faktor
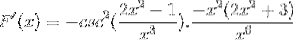
Značky jsou zjednodušené a fungují. Dát cestu plně odvozenému výrazu
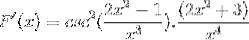
Reference
- Trigonometrická řada, svazek 1. A. Zygmund. Cambridge University Press, 2002
- Počet jedné proměnné. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. listopadu 2008
- Kalkul s trigonometrií a analytickou geometrií. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
- Analýza více proměnných. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. prosince. 2010
- Systémová dynamika: modelování, simulace a řízení mechatronických systémů. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. března 2012
- Matematika a modelování. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. ledna 1999



Zatím žádné komentáře