
Koeficient tepelné roztažnosti, typy a cvičení

The teplotní roztažnost Jedná se o zvětšení nebo změnu různých metrických dimenzí (například délky nebo objemu), které prochází fyzické tělo nebo předmět. K tomuto procesu dochází v důsledku zvýšení teploty obklopující materiál. V případě lineární dilatace dochází k těmto změnám v jedné dimenzi.
Koeficient této expanze lze měřit porovnáním hodnoty velikosti před a po procesu. Některé materiály trpí opakem tepelné roztažnosti; to znamená, že se stane „negativním“. Tento koncept navrhuje, aby se některé materiály při vystavení určitým teplotám stáhly.
U pevných látek se k popisu jejich roztažnosti používá koeficient lineární roztažnosti. Na druhou stranu pro kapaliny se k výpočtu používá objemový koeficient roztažnosti..
V případě krystalizovaných pevných látek, je-li to izometrické, bude expanze obecná ve všech rozměrech krystalu. Pokud to není izometrické, lze ve sklenici najít různé koeficienty roztažnosti a při změně teploty se změní jeho velikost..
Rejstřík článků
- 1 Koeficient tepelné roztažnosti
- 2 Negativní tepelná roztažnost
- 3 typy
- 3.1 Lineární dilatace
- 3.2 Objemová dilatace
- 3.3 Povrchová nebo plošná dilatace
- 4 příklady
- 4.1 První cvičení (lineární dilatace)
- 4.2 Druhé cvičení (povrchní dilatace)
- 5 Proč dochází k dilataci?
- 6 Reference
Koeficient tepelné dilatace
Koeficient tepelné roztažnosti (Y) je definován jako poloměr změny, kterým materiál prošel změnou jeho teploty. Tento koeficient je reprezentován symbolem α pro pevné látky a β pro kapaliny a je veden Mezinárodním systémem jednotek.
Koeficienty tepelné roztažnosti se mění, pokud jde o pevné látky, kapaliny nebo plyny. Každý z nich má jiné zvláštnosti.
Například expanzi tělesa lze vidět po délce. Objemový koeficient je jedním z nejzákladnějších z hlediska tekutin a změny jsou patrné ve všech směrech; tento koeficient se také používá při výpočtu expanze plynu.
Negativní tepelná roztažnost
Negativní tepelná roztažnost nastává u některých materiálů, které se místo zvětšování s vysokými teplotami smršťují kvůli nízkým teplotám.
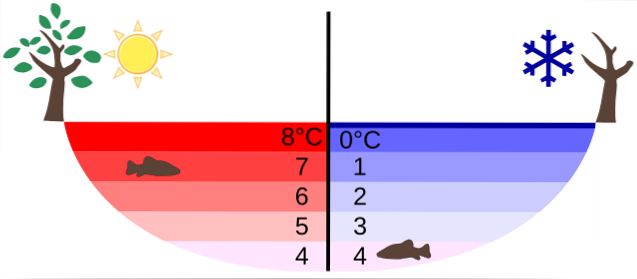
Tento typ tepelné roztažnosti je obvykle vidět v otevřených systémech, kde jsou pozorovány směrové interakce - jako je tomu v případě ledu - nebo v komplexních sloučeninách - jako je tomu u některých zeolitů, mimo jiné Cu20..
Stejně tak některé výzkumy ukázaly, že negativní tepelná roztažnost se vyskytuje také v jednosložkových mřížích v kompaktní formě a s centrální silovou interakcí.
Jasný příklad negativní tepelné roztažnosti lze vidět, když přidáme led do sklenice vody. V tomto případě vysoká teplota kapaliny na ledu nezpůsobuje žádné zvětšení velikosti, ale spíše se zmenší velikost ledu..
Typy
Při výpočtu expanze fyzického objektu je třeba vzít v úvahu, že v závislosti na změně teploty se uvedený objekt může zvětšit nebo zmenšit jeho velikost..
Některé objekty nevyžadují pro změnu své velikosti drastickou změnu teploty, takže je pravděpodobné, že hodnota vrácená výpočty je průměrná.
Jako každý proces, tepelná roztažnost je rozdělena do několika typů, které vysvětlují každý jev zvlášť. V případě pevných látek jsou typy tepelné roztažnosti lineární roztažnost, objemová roztažnost a povrchová roztažnost.
Lineární dilatace
V lineární dilataci převládá jedna variace. V tomto případě je jedinou jednotkou, která prochází změnou, výška nebo šířka objektu.
Snadný způsob výpočtu tohoto typu dilatace je porovnáním hodnoty velikosti před změnou teploty s hodnotou velikosti po změně teploty..
Objemová dilatace
V případě objemové roztažnosti je možné ji vypočítat porovnáním objemu kapaliny před změnou teploty s objemem kapaliny po změně teploty. Vzorec pro jeho výpočet je:
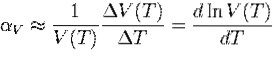
Povrchová nebo plošná dilatace
V případě povrchové dilatace je pozorováno zvětšení plochy těla nebo předmětu v důsledku změny jeho teploty při 1 ° C.
Tato expanze funguje pro pevné látky. Pokud máte také lineární koeficient, uvidíte, že velikost objektu bude dvakrát větší. Vzorec pro jeho výpočet je:
NAF = A0 [1 + YA (T.F - T0)]
V tomto výrazu:
γ = koeficient plošného roztažení [° C-1]
NA0 = Počáteční plocha
NAF = Konečná plocha
T0 = Počáteční teplota.
TF = Konečná teplota
Rozdíl mezi plošnou dilatací a lineární dilatací spočívá v tom, že v první z nich vidíte zvětšení změny v oblasti objektu a ve druhé je změna jednotkovou měrnou jednotkou (například délka nebo šířka fyzické objekt).
Příklady
První cvičení (lineární dilatace)
Kolejnice, které tvoří trať ocelového vlaku, mají délku 1500 m. Jaká bude zeměpisná délka, když teplota klesne z 24 na 45 ° C?
Řešení
Data:
Lο (počáteční délka) = 1500 m
LF (konečná délka) = ?
Tο (počáteční teplota) = 24 ° C
TF (konečná teplota) = 45 ° C
α (koeficient lineární roztažnosti odpovídající oceli) = 11 x 10-6 ° C-1
Data jsou nahrazena následujícím vzorcem:
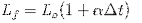
Nejprve však musíte znát hodnotu teplotního rozdílu, abyste mohli tato data zahrnout do rovnice. K dosažení tohoto rozdílu je třeba odečíst nejvyšší teplotu od nejnižší.
Δt = 45 ° C - 24 ° C = 21 ° C
Jakmile jsou tyto informace známy, je možné použít předchozí vzorec:
Lf = 1 500 m (1 + 21 ° C, 11 x 10-6 ° C-1)
Lf = 1 500 m (1 + 2,31 x 10-4)
Lf = 1 500 m (1 000231)
Lf = 1500,3465 m
Druhé cvičení (povrchní dilatace)
Na střední škole má sklad skla plochu 1,4 m ^ 2, pokud je teplota 21 ° C. Jaká bude jeho konečná plocha, když teplota vzroste na 35 ° C?
Řešení
Af = A0 [1 + (Tf - T0)]
Af = 1,4 mdva [1] 204,4 x 10-6]
Af = 1,4 mdva . 1 0002044
Af = 1,40028616 mdva
Proč dochází k dilataci?
Každý ví, že veškerý materiál je složen z různých subatomárních částic. Změnou teploty, jejím zvýšením nebo snížením, tyto atomy zahájí proces pohybu, který může změnit tvar objektu..
Když se teplota zvýší, molekuly se začnou rychle pohybovat v důsledku zvýšení kinetické energie, a proto se zvýší tvar nebo objem objektu..
V případě záporných teplot se stane opak, v tomto případě má objem objektu tendenci se snižovat kvůli nízkým teplotám..
Reference
- Lineární, povrchní a objemová dilatace - cvičení. Vyřešeno Obnoveno 8. května 2018, z Fisimat: fisimat.com.mx
- Povrchní dilatace - vyřešená cvičení. Citováno dne 8. května 2018 z webu Fisimat: fisimat.com.mx
- Teplotní roztažnost. Citováno dne 8. května 2018 z Encyklopedie Britannica: britannica.com
- Teplotní roztažnost. Citováno dne 8. května 2018 z Hyper Physics Concepts: hyperphysics.phy-astr.gsu.edu
- Teplotní roztažnost. Citováno dne 8. května 2018 z webu Lumen Learning: courses.lumenlearning.com
- Teplotní roztažnost. Citováno dne 8. května 2018 z Hypertextbooku The Physics: physics.info
- Teplotní roztažnost. Citováno dne 8. května 2018 z Wikipedie: en.wikipedia.org.



Zatím žádné komentáře