Metoda syntetického dělení a řešená cvičení

The syntetické dělení je jednoduchý způsob, jak rozdělit libovolný polynom P (x) jedním z tvarů d (x) = x - c. Například polynom P (x) = (x⁵+3x⁴-7x³+2x^dva-8x + 1) lze reprezentovat jako násobení dvou nejjednodušších polynomů (x + 1) a (x⁴ + 2x³).

Je to velmi užitečný nástroj, protože kromě toho, že nám umožňuje rozdělit polynomy, umožňuje nám také vyhodnotit polynom P (x) na jakémkoli čísle c, což nám zase říká přesně, zda je dané číslo nula nebo ne polynomiální.

Díky algoritmu dělení víme, že pokud máme dva polynomy P (x) Y d (x) nekonstanty, existují polynomy q (x) Y r (x) jedinečné takové, že platí, že P (x) = q (x) d (x) + r (x), kde r (x) je nula nebo menší než q (x). Tyto polynomy jsou známé jako kvocient a zbytek nebo zbytek.

V případech, kdy má polynom d (x) tvar x- c, syntetické dělení nám dává krátký způsob, jak zjistit, kdo jsou q (x) a r (x).

Rejstřík článků

• 1 Metoda syntetického dělení
• 2 Vyřešená cvičení
  • 2.1 - Příklad 1
  • 2.2 - Příklad 2
  • 2.3 - Příklad 3
  • 2.4 - Příklad 4
• 3 Odkazy

Metoda syntetického dělení

Nechť P (x) = a_nXⁿ+na_n-1X^n-1+… + A₁x + a₀ polynom, který chceme rozdělit a d (x) = x-c dělitel. Při dělení metodou syntetického dělení postupujeme následovně:

1 - Do prvního řádku napíšeme koeficienty P (x). Pokud se nějaká mocnina X neobjeví, dáme jako její koeficient nulu.

2- Ve druhé řadě nalevo od a_n umístíme c a nakreslíme dělicí čáry, jak je znázorněno na následujícím obrázku:

3 - Snížíme vedoucí koeficient do třetí řady.

V tomto výrazu b_n-1= a_n

4- Násobíme c vedoucím koeficientem b_n-1 a výsledek zapíšeme do druhého řádku, ale o jeden sloupec vpravo.

5- Přidáme sloupec, do kterého zapíšeme předchozí výsledek, a výsledek umístíme pod tento součet; to znamená ve stejném sloupci třetí řádek.

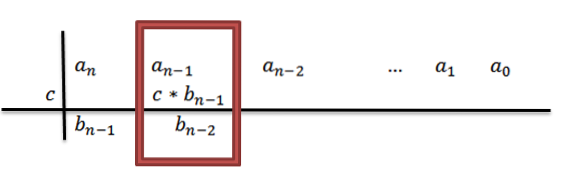
Při přidávání máme jako výsledek_n-1+c * b_n-1, které pro pohodlí budeme nazývat b_n-2

6- Násobíme c předchozím výsledkem a výsledek zapíšeme napravo do druhého řádku.

7- Opakujeme kroky 5 a 6, dokud nedosáhneme koeficientu a₀.

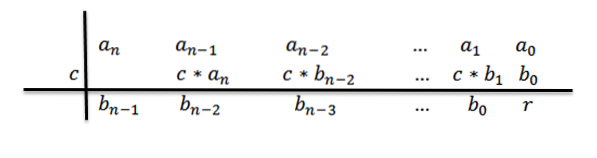
8- Píšeme odpověď; to je kvocient a zbytek. Jelikož dělíme polynom stupně n polynomem stupně 1, máme, že podíl by byl stupně n-1.

Koeficienty kvocientového polynomu budou čísla ve třetím řádku s výjimkou posledního, což bude zbytek nebo zbytek dělení.

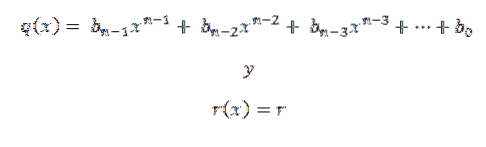
Vyřešená cvičení

- Příklad 1

Proveďte následující dělení metodou syntetického dělení:

(X⁵+3x⁴-7x³+2x^dva-8x + 1): (x + 1).

Řešení

Nejprve napíšeme dividendové koeficienty následovně:

Potom napíšeme c na levou stranu, do druhé řady, spolu s dělicími čarami. V tomto příkladu c = -1.

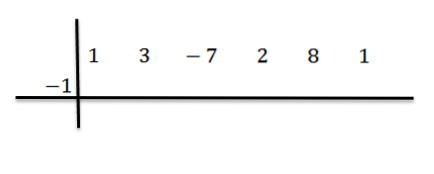
Snižujeme počáteční koeficient (v tomto případě b_n-1 = 1) a vynásobíme to -1:

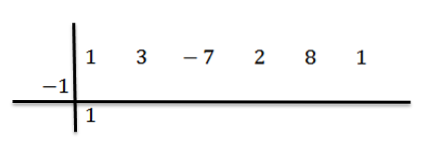
Výsledek zapíšeme vpravo do druhého řádku, jak je znázorněno níže:

Přidáme čísla ve druhém sloupci:

Násobíme 2 číslem -1 a výsledek zapíšeme do třetího sloupce, druhého řádku:

Přidáme do třetího sloupce:

Postupujeme stejným způsobem, dokud nedosáhneme posledního sloupce:

Máme tedy, že poslední získané číslo je zbytek dělení a zbývající čísla jsou koeficienty kvocientového polynomu. Toto je napsáno takto:

Pokud chceme ověřit, že je výsledek správný, stačí ověřit, zda je pravdivá následující rovnice:

P (x) = q (x) * d (x) + r (x)

Můžeme tedy zkontrolovat, že získaný výsledek je správný.

- Příklad 2

Následující dělení polynomů proveďte metodou syntetického dělení

(7x³-x + 2): (x + 2)

Řešení

V tomto případě máme výraz x^dva nezobrazí se, takže jako jeho koeficient napíšeme 0. Polynom by tedy byl 7x³+0x^dva-x + 2.

Píšeme jejich koeficienty za sebou, to je:

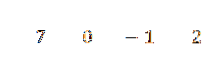
Do druhé řady napíšeme na levou stranu hodnotu C = -2 a nakreslíme dělicí čáry.

Snížíme přední koeficient b_n-1 = 7 a vynásobte jej číslem -2, výsledek zapište do druhého řádku doprava.

Přidáme a pokračujeme, jak již bylo vysvětleno, dokud nedosáhneme posledního termínu:

V tomto případě je zbytek r (x) = - 52 a získaný kvocient je q (x) = 7x^dva-14x + 27.

- Příklad 3

Další způsob, jak použít syntetické dělení, je následující: Předpokládejme, že máme polynom P (x) stupně n a chceme vědět, co je jeho hodnota, a to tak, že jej vyhodnotíme na x = c.

Podle algoritmu dělení máme, že můžeme psát polynom P (x) následovně:

V tomto výrazu q (x) a r (x) jsou kvocient a zbytek. Nyní, pokud d (x) = x- c, při hodnocení v c v polynomu získáme následující:

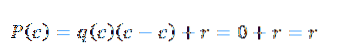
Z tohoto důvodu zbývá najít pouze r (x) a můžeme to udělat díky syntetickému dělení.

Například máme polynom P (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x^dva-37x-37 a chceme vědět, jaká je jeho hodnota, tím, že ji vyhodnotíme na x = 5. Za tímto účelem rozdělíme mezi P (x) a d (x) = x -5 metodou syntetického dělení:

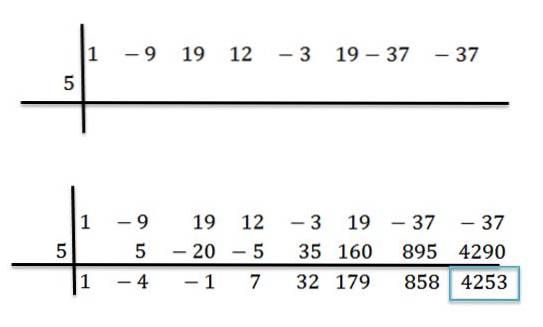
Jakmile jsou operace hotové, víme, že můžeme psát P (x) následujícím způsobem:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x^dva +179x + 858) * (x-5) + 4253

Při jeho hodnocení proto musíme:

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (5-5) + 4253

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (0) + 4253

P (5) = 0 + 4253 = 4253

Jak vidíme, je možné použít syntetické dělení k nalezení hodnoty polynomu vyhodnocením v c namísto jednoduchého nahrazení c za x. 

Pokud bychom se pokusili vyhodnotit P (5) tradičním způsobem, byli bychom nuceni provést nějaké výpočty, které mají tendenci být zdlouhavé.

- Příklad 4

Algoritmus dělení pro polynomy platí také pro polynomy se složitými koeficienty a v důsledku toho máme, že metoda syntetického dělení funguje i pro takové polynomy. Dále uvidíme příklad.

Použijeme metodu syntetického dělení, abychom ukázali, že z = 1+ 2i je nula polynomu P (x) = x³+ (1 + i) x^dva -(1 + 2i) x + (15 + 5i); to znamená, že zbytek dělení P (x) d (x) = x - z se rovná nule.

Postupujeme jako dříve: do prvního řádku napíšeme koeficienty P (x), do druhého napíšeme z a nakreslíme dělicí čáry.

Provádíme rozdělení jako dříve; tohle je:

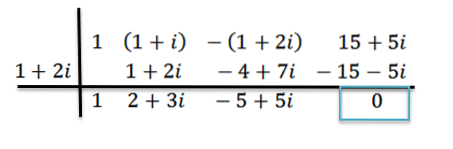
Vidíme, že zbytek je nula; proto jsme dospěli k závěru, že z = 1+ 2i je nula P (x).

Reference

1. Baldor aurelio. Algebra. Grupo Editorial Patria.
2. Demana, Waits, Foley a Kennedy. Precalculus: Graphical, numerical, algebraic 7. ed. Pearson Education.
3. Flemming W & Varserg D. Algebra a trigonometrie s analytickou geometrií. Hala Prentice
4. Michael Sullivan. Předpočet 4. vyd. Pearson Education.
5. Červené. Armando O. Algebra 1 6. vyd. Athenaeum.