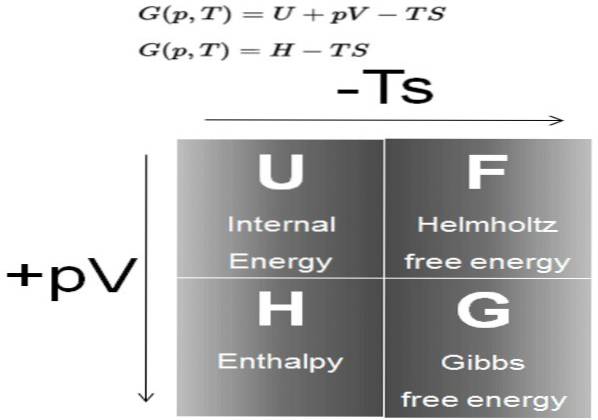
The Gibbsova volná energie (běžně nazývaný G) je termodynamický potenciál definovaný jako rozdíl entalpie H, minus součin teploty T, entropií S systému:
G = H - TS
Gibbsova volná energie se měří v joulech (podle mezinárodního systému), v ergs (pro cegesimální systém jednotek), v kaloriích nebo v elektronvoltech (pro elektrovolty).
V procesech, které se vyskytují při konstantním tlaku a teplotě, je variace Gibbsovy volné energie ΔG = ΔH - T ΔS. V takových procesech představuje (G) energii dostupnou v systému, kterou lze přeměnit na práci.
Například při exotermických chemických reakcích entalpie klesá, zatímco entropie roste. Ve funkci Gibbs jsou tyto dva faktory potlačeny, ale pouze když se Gibbsova energie sníží, dojde k reakci spontánně..
Pokud je tedy variace G negativní, proces je spontánní. Když Gibbsova funkce dosáhne svého minima, systém dosáhne stabilního rovnovážného stavu. Stručně řečeno, v procesu, pro který tlak a teplota zůstávají konstantní, můžeme potvrdit:
- Pokud je proces spontánní, pak ΔG < 0
- Když je systém v rovnováze: ΔG = 0
- V spontánním procesu G stoupá: ΔG> 0.
Rejstřík článků
Gibbsova volná energie (G) se vypočítá pomocí definice uvedené na začátku:
G = H - T⋅S
Entalpie H je zase termodynamický potenciál definovaný jako:
H = U + P V
Dále bude provedena podrobná analýza, aby bylo možné znát nezávislé proměnné, jejichž funkcí je Gibbsova energie:
1- Z prvního zákona termodynamiky máme, že vnitřní energie U souvisí s entropií S systému a jeho objemem V pro reverzibilní procesy prostřednictvím diferenciálního vztahu:
dU = dQ - dW = TdS - PdV
Z této rovnice vyplývá, že vnitřní energie U je funkcí proměnných S a V:
U = U (S, V)
2- Vycházíme z definice H a vezmeme-li diferenciál, získáme:
dH = dU + d (P V) = dU + VdP + PdV
3 - Dosazením výrazu pro dU získaného v (1) máme:
dH = TdS - PdV + VdP + PdV = TdS + VdP
Z toho lze vyvodit, že entalpie H závisí na entropii S a tlaku P, tj.
H = H (S, P)
4 - Nyní se vypočítá celkový rozdíl Gibbsovy volné energie získáním:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
Kde dH byl nahrazen výrazem nalezeným v (3).
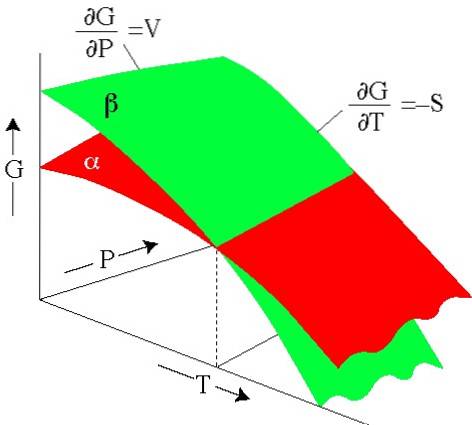
5- Nakonec při zjednodušení získáme: dG = VdP - SdT, je jasné, že volná energie G závisí na tlaku a teplotě T jako:
G = G (P, T)
Z analýzy v předchozí části vyplývá, že vnitřní energie systému je funkcí entropie a objemu:
U = U (S, V)
Pak rozdíl NEBO bude:
dU = ∂SU |PROTI dS + ∂PROTIU |S dV = TdS - PdV
Z tohoto částečného derivačního výrazu lze odvodit tzv. Maxwellovy termodynamické vztahy. Částečné derivace platí, když funkce závisí na více než jedné proměnné a lze je snadno vypočítat použitím věty v následující části.
∂PROTIT |S = -∂SP |PROTI
Abychom dospěli k tomuto vztahu, Clairaut-Schwarzova věta o parciálních derivátech, kde se uvádí:
„Smíšené deriváty druhého řádu s vyměněnými proměnnými jsou stejné, pokud jsou odvozené funkce spojité a diferencovatelné.“.
Na základě toho, co je uvedeno v bodě 3 předchozí části:
H = H (S, P) a dH = TdS + VdP
Lze jej získat:
∂PT |S = ∂SV |P
Podobně postupujeme s Gibbsovou volnou energií G = G (P, T) as Helmholtzovou volnou energií F = F (T, V) získat další dva Maxwellovy termodynamické vztahy.
1- Souvisí s vnitřní energií U: ∂PROTIT |S = -∂SP |PROTI
2 - Ten získaný z entalpie H: ∂PT |S = ∂SV |P
3 - Souvisí s Helmholtzovou energií F: ∂TP |PROTI = ∂PROTIS |T
4 - Souvisí s volnou energií Gibbs G: ∂TV |P = -∂PS |T
Vypočítejte variaci Gibbsovy volné energie pro 2 moly ideálního plynu při teplotě 300 K během izotermické expanze, při které se systém přemění z počátečního objemu 20 litrů na konečný objem 40 litrů.
Připomínajíc definici Gibbsovy volné energie máme:
G = H - TS
Konečná variace F pak bude:
ΔG = ΔH - T ΔS, protože ΔT = 0
V ideálních plynech entalpie závisí pouze na její absolutní teplotě, ale protože se jedná o izotermický proces, pak ΔH = 0 a ΔG = - T ΔS.
Pro ideální plyny je změna entropie izotermického procesu:
ΔS = nR ln (Vdva/ V1)
To platí pro případ tohoto cvičení:
ΔS = 2 moly x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Pak můžeme dosáhnout změny Helmholtzovy energie:
ΔG = - 300 K x 11,53 J / K = -3457,70 J.
Vezmeme-li v úvahu, že Gibbsova volná energie je funkcí teploty a tlaku G = G (T, P); určit variaci G během procesu, ve kterém se teplota nemění (izotermicky) pro n molů ideálního monatomického plynu.
Jak je uvedeno výše, změna Gibbsovy energie závisí pouze na změně teploty T a objemu V, takže její nekonečně malá variace se vypočítá podle:
dG = -SdT + VdP
Pokud však jde o proces, při kterém je teplota konstantní, pak dF = + VdP, takže konečná kolísání tlaku ΔP vede ke změně Gibbsovy energie dané:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = + n R T ln (ΔP)
Pomocí rovnice ideálního plynu:
P V = n R T
Během izotermického procesu dochází k tomu, že:
d (P V) = P dV + V dP = 0
To je:
dP / P = - dV / V
Takže výše uvedený výsledek lze zapsat jako funkci variace hlasitosti ΔV:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = - ∫ (n R T) dV / V = -n R T ln (ΔV)
Vzhledem k následující chemické reakci:
Ndva0 (g) + (3/2) O.dva (g) ↔️ 2NOdva (g) při teplotě T = 298 K.
Najděte variantu Gibbsovy volné energie a pomocí získaných výsledků uveďte, zda se jedná o spontánní proces.
Tady jsou kroky:
- Krok první: Entalpie reakce
ΔHr = 2 * ΔH (NOdva (g)) - ΔH (Ndva0 (g)) = 2 * 33,2-81,6 = -15,2kJ / mol
- Druhý krok: variace reakční entropie
ΔSr = 2 * S (Čdva (g)) - S (čdva0 (g)) - (3/2) S (O.dva (g)) = 2 * 240,1 - 220,1 - 1,5 * 205,2 = -47,7 J / (mol * K).
- Třetí krok: variace funkce Gibbs
Tato hodnota určí rovnováhu mezi klesající energií a rostoucí entropií, aby bylo možné zjistit, zda je reakce spontánní nebo ne.
ΔGr = ΔHr - T ΔSr = -15,2 -298 * (- 47,7) = -985,4 J / mol
Jelikož se jedná o negativní variaci Gibbsovy energie, lze usoudit, že se jedná o spontánní reakci při teplotě 298 K = 25 ° C.
Zatím žádné komentáře