
Vzorkování chybových vzorců a rovnic, výpočet, příklady
The chyba vzorkování nebo chyba vzorku Ve statistikách je to rozdíl mezi střední hodnotou vzorku a střední hodnotou celkové populace. Pro ilustraci této představy si představme, že celková populace města je jeden milion lidí, z nichž je požadována průměrná velikost obuvi, pro kterou je odebrán náhodný vzorek jednoho tisíce lidí.
Průměrná velikost, která vyplyne ze vzorku, se nemusí nutně shodovat s velikostí celkové populace, ačkoli pokud vzorek není předpjatý, hodnota musí být blízká. Tento rozdíl mezi střední hodnotou vzorku a hodnotou celkové populace je chybou vzorkování.
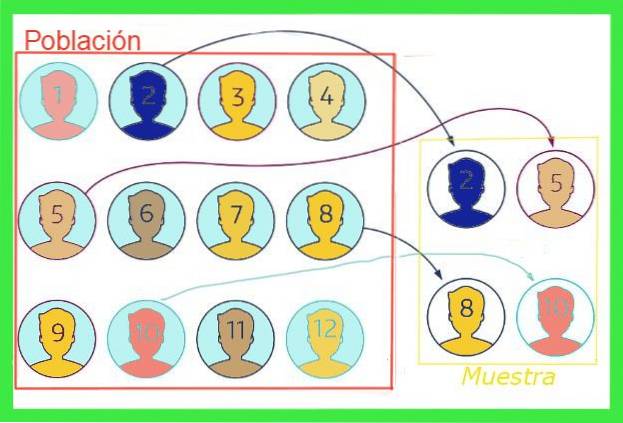
Průměrná hodnota celkové populace obecně není známa, ale existují techniky ke snížení této chyby a vzorce pro odhad chybová marže vzorkování které budou zveřejněny v tomto článku.
Rejstřík článků
- 1 Vzorce a rovnice
- 2 Jak vypočítat chybu vzorkování
- 2.1 Pro hladinu spolehlivosti γ
- 3 příklady
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 3.3 - Příklad 3
- 3.4 - Příklad 4
- 3.5 - Cvičení 5
- 4 Odkazy
Vzorce a rovnice
Řekněme, že chcete znát průměrnou hodnotu určité měřitelné charakteristiky X v populaci velikosti N, ale jak N je velké číslo, není možné provést studii o celkové populaci, pak přistoupíme k a nejistý vzorek velikosti n<
Střední hodnota vzorku je označena
Předpokládejme, že berou m vzorky z celkové populace N, všechny stejné velikosti n se středními hodnotami
Tyto střední hodnoty nebudou navzájem identické a budou se pohybovat kolem střední hodnoty populace μ. The rozpětí chyby vzorkování E označuje očekávané oddělení středních hodnot
The standardní odchylka chyby ε vzorek velikosti n to je:
ε = σ / √n
kde σ je směrodatná odchylka (druhá odmocnina rozptylu), která se vypočítá pomocí následujícího vzorce:
σ = √ [(x -
Význam standardní odchylka chyby ε je následující:
The střední hodnota
Jak vypočítat chybu vzorkování
V předchozí části byl uveden vzorec pro nalezení rozsah chyb Standard vzorku velikosti n, kde slovo standard naznačuje, že se jedná o míru chyby se spolehlivostí 68%.
To znamená, že pokud bylo odebráno mnoho vzorků stejné velikosti n, 68% z nich uvede průměrné hodnoty
Existuje jednoduché pravidlo zvané pravidlo 68-95-99.7 což nám umožňuje najít rozpětí chyba vzorkování E pro úrovně spolehlivosti 68%, 95% Y 99,7% snadno, protože tato marže je 1⋅ε, 2⋅ε a 3⋅ε resp.
Pro jistotu y
Jestli on úroveň spolehlivosti γ není nic z výše uvedeného, pak je chyba vzorkování standardní odchylkou σ vynásobený faktorem Zγ, který se získá následujícím postupem:
1. - Nejprve hladina významnosti α který se počítá z úroveň spolehlivosti γ pomocí následujícího vztahu: α = 1 - γ
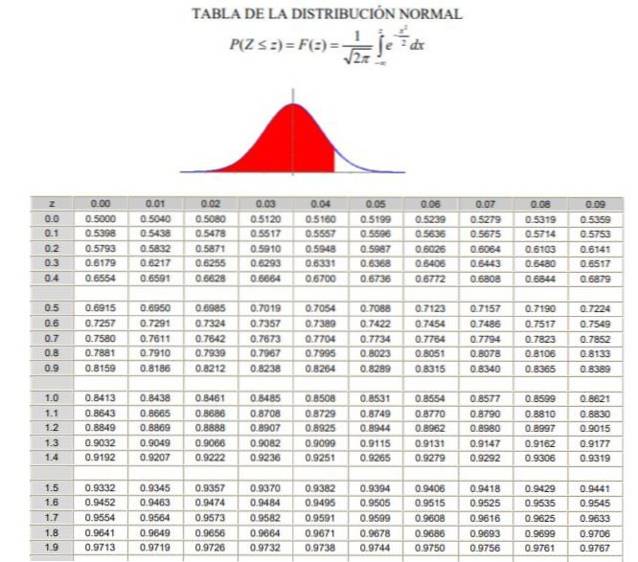
2. - Poté musíte vypočítat hodnotu 1 - α / 2 = (1 + γ) / 2, což odpovídá akumulované normální frekvenci mezi -∞ a Zγ, v normálním nebo standardizovaném Gaussově rozdělení F (z), jehož definici lze vidět na obrázku 2.
3.- Rovnice je vyřešena F (Zγ) = 1 - α / 2 pomocí tabulek normálního rozdělení (kumulativní) F, nebo pomocí počítačové aplikace, která má inverzní standardizovanou Gaussovu funkci F-1.
V druhém případě máme:
Zγ = G-1(1 - α / 2).
4.- Nakonec se tento vzorec použije pro chybu vzorkování s úrovní spolehlivosti γ:
E = Zγ⋅(σ / √n)
Příklady
- Příklad 1
Vypočítejte standardní odchylka v průměrné hmotnosti vzorku 100 novorozenců. Výpočet průměrné hmotnosti byl
Řešení
The standardní odchylka to je ε = σ / √n = (1500 kg) / √100 = 0,15 kg. Což znamená, že z těchto údajů lze odvodit, že hmotnost 68% novorozenců se pohybuje mezi 2950 kg a 3,25 kg.
- Příklad 2
Určit mez chyby vzorkování E a hmotnostní rozsah 100 novorozenců s 95% úrovní spolehlivosti, pokud je průměrná hmotnost 3 100 kg se standardní odchylkou σ = 1 500 kg.
Řešení
Pokud pravidlo 68; 95; 99,7 → 1⋅ε; 2⋅ε; 3⋅ε, ty máš:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
To znamená, že 95% novorozenců bude mít hmotnost mezi 2 800 kg a 3 400 kg.
- Příklad 3
Určete rozsah hmotností novorozenců z příkladu 1 s mírou spolehlivosti 99,7%.
Řešení
Chyba vzorkování s 99,7% spolehlivostí je 3 σ / √n, což je pro náš příklad E = 3 * 0,15 kg = 0,45 kg. Odtud lze odvodit, že 99,7% novorozenců bude mít hmotnost mezi 2 650 kg a 3 550 kg.
- Příklad 4
Určete faktor Zγ pro úroveň spolehlivosti 75%. Určete rozpětí chyby vzorkování s touto úrovní spolehlivosti pro případ uvedený v příkladu 1.
Řešení
The úroveň spolehlivosti to je y = 75% = 0,75, což souvisí s úroveň významnosti α prostřednictvím vztahu y= (1 - α), takže úroveň významnosti je α = 1 - 0,75 = 0,25.
To znamená, že kumulativní normální pravděpodobnost mezi -∞ a Zγ to je:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Co odpovídá hodnotě Zγ 1.1503, jak je znázorněno na obrázku 3.
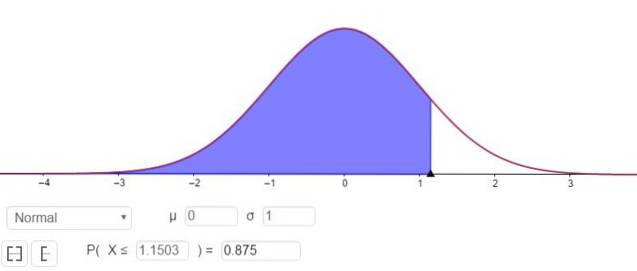
To znamená, že chyba vzorkování je E = Zγ⋅(σ / √n)= 1.15⋅(σ / √n).
Při použití na data z příkladu 1 dává chybu:
E = 1,15 * 0,15 kg = 0,17 kg
S úrovní spolehlivosti 75%.
- Cvičení 5
Jaká je úroveň spolehlivosti, pokud Zα / 2 = 2.4 ?
Řešení
P (Z ≤ Zα / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Úroveň významnosti je:
α = 0,0164 = 1,64%
A konečně zůstává úroveň spolehlivosti:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Reference
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Levin, R. 1988. Statistiky pro správce. 2. místo Edice. Hala Prentice.
- Sudman, S. 1982. Kladení otázek: Praktický průvodce návrhem dotazníku. San Francisco. Baskytara Jossey.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.
- Wonnacott, T.H. a R.J. Wonnacott. 1990. Úvodní statistika. 5. vyd. Wiley
- Wikipedia. Chyba vzorkování. Obnoveno z: en.wikipedia.com
- Wikipedia. Okraj chyby. Obnoveno z: en.wikipedia.com


Zatím žádné komentáře