
Popisná historie statistiky, charakteristika, příklady, pojmy
The Deskriptivní statistika je obor statistiky, který je zodpovědný za shromažďování a organizování informací o chování systémů s mnoha prvky, obecně známých pod jménem populace.
K tomu využívá numerické a grafické techniky, pomocí nichž poskytuje informace, aniž by předpovídal nebo vyvodil závěry o populaci, ze které pochází..

Rejstřík článků
- 1 Historie
- 1.1 Starověký věk
- 1.2 Renesance
- 1.3 Moderní doba
- 2 Charakteristika popisné statistiky
- 3 K čemu slouží popisná statistika?
- 3.1 Ekonomika
- 3.2 Fyzika a mechanika
- 3.3 Medicína
- 3.4 Výživa
- 4 Příklady popisné statistiky
- 4.1 Příklad 1
- 4.2 Příklad 2
- 4.3 Příklad 3
- 5 Základní pojmy popisné statistiky
- 5.1 Obyvatelstvo
- 5.2 Ukázka
- 5.3 Proměnná
- 5.4 Opatření ústřední tendence
- 5.5 Měření disperze
- 6 Témata zájmu
- 7 Reference
Příběh
Starý věk
Statistika má původ v lidské potřebě organizovat informace nezbytné pro její přežití a pohodu a předvídat události, které ji ovlivňují. Velké civilizace starověku zanechaly záznamy o osadnících, vybraných daních, množství úrody a velikosti armád.
Například během své dlouhé vlády Ramses II. (1279–1213 př. N. L.) Nařídil sčítání zemí a obyvatel v Egyptě, které mělo v té době asi 2 miliony obyvatel..
Stejně tak Bible vypráví, že Mojžíš provedl sčítání lidu, aby zjistil, kolik vojáků mělo dvanáct izraelských kmenů.
Také ve starověkém Řecku se počítali lidé a zdroje. Římané, pozoruhodní svou vysokou organizací, pravidelně registrovali obyvatelstvo a každých pět let vypracovávali sčítání, včetně území a zdrojů..
renesance
Po úpadku Říma byly důležité statistické záznamy vzácné až do příchodu renesance, kdy se statistika znovu objevila jako pomůcka při rozhodování.
Na konci sedmnáctého století se zrodila teorie pravděpodobností, výsledek sklonu lidí k hazardním hrám, což dalo statistice matematickou přesnost, která z ní udělala samostatnou vědu.
Moderní doba
Nový impuls přišel s teorií chyb a nejmenších čtverců v 19. století, po které následovala metoda korelace mezi proměnnými, aby bylo možné kvantitativně posoudit vztah mezi nimi..
Až do konce 20. století se statistika rozšířila do každého odvětví vědy a techniky jako nepostradatelný nástroj při řešení problémů..
Popisné statistické charakteristiky
Popisné statistiky se vyznačují:
- Uspořádejte shromážděné informace ve formě dat a grafů. Grafy mohou být různorodé: histogramy, frekvenční polygony, kruhové diagramy a další..
- Distribuujte data ve frekvenčních rozsazích, abyste usnadnili jejich správu. Pomocí aritmetiky vyhledejte nejreprezentativnější hodnoty dat pomocí opatření centrální tendence a analyzujte jejich rozptyl.
- Určete tvar distribucí, jejich symetrii, jsou-li vycentrovány nebo zkoseny a jsou-li špičaté nebo spíše zploštělé.
K čemu jsou popisné statistiky?
Kdykoli je třeba shromažďovat, organizovat a prezentovat údaje, jsou popisné statistiky nezbytné v oblastech vědy, které se zabývají mnoha prvky a veličinami, a také v mnoha lidských činnostech: ekonomie, politika, zdraví, sport a další..
Zde jsou nějaké příklady:
Ekonomika
Popisná statistika se zabývá důsledným zaznamenáváním a uspořádáním údajů o populacích a jejich věku, příjmech, investicích, výdělcích a výdajích. Tímto způsobem vlády a instituce plánují zlepšení a vhodným způsobem investují zdroje..
S jeho pomocí jsou sledovány nákupy, prodeje, návratnost a efektivita služeb. Z tohoto důvodu jsou při rozhodování zásadní statistiky.
Fyzika a mechanika
Fyzika a mechanika používají statistiku ke studiu kontinuálních médií, která se skládají z velkého počtu částic, jako jsou atomy a molekuly. Ukazuje se, že není možné sledovat každou z nich samostatně..
Ale studium globálního chování systému (například části plynu) z makroskopického hlediska je možné najít průměry a definovat makroskopické proměnné, aby bylo možné znát jejich vlastnosti. Příkladem toho je kinetická teorie plynů.
Lék
Je základním nástrojem při sledování nemocí, od jejich vzniku a během jejich vývoje, jakož i účinnosti léčby.
Statistiky, které popisují míru morbidity, míru vyléčení, inkubační dobu nebo dobu vývoje onemocnění, věk, ve kterém se obvykle objevuje, a podobné údaje jsou nezbytné při navrhování nejúčinnějších způsobů léčby..
Výživa
Jednou z mnoha aplikací popisné statistiky je zaznamenávání a objednávání údajů o spotřebě potravin v různých populacích: jejich množství, kvalita a které jsou nejvíce konzumovány, kromě mnoha dalších pozorování, které zajímají odborníky..
Popisné statistické příklady
Tady je několik příkladů, které ilustrují, jak užitečné jsou nástroje popisné statistiky, které vám pomohou při rozhodování:
Příklad 1

Institucionální zlepšení plánují vzdělávací orgány dané země. Předpokládejme, že budete implementovat nový systém školní jídelny.
K tomu je nezbytné mít k dispozici údaje o studentské populaci, například o počtu studentů na ročníku, jejich věku, pohlaví, výšce, hmotnosti a socioekonomickém postavení. Tyto informace jsou poté prezentovány ve formě tabulek a grafů..
Příklad 2
Aby udrželi přehled o místním fotbalovém týmu a vytvářeli nové autogramiády, manažeři sledují počet odehraných, vyhraných, nerozhodných a ztracených her, stejně jako počet gólů, střelců a způsob, jakým dokázali skórovat: volný kop, poloviční soud, pokuty, mimo jiné s levou nebo pravou nohou.
Příklad 3
Zmrzlinový salon má několik příchutí zmrzliny a chce zlepšit svůj prodej, proto majitelé provedou studii, kde spočítají počet zákazníků, rozdělí je do skupin podle pohlaví a věkových skupin.
V této studii je například zaznamenána oblíbená zmrzlinová příchuť a nejprodávanější prezentace. A se shromážděnými údaji plánují nákupy příchutí a nádob a příslušenství nezbytných pro jejich přípravu..
Základy popisné statistiky
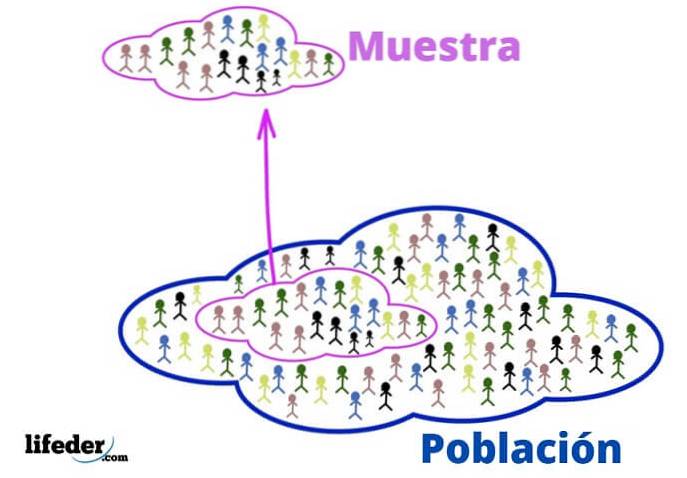
Tyto základní pojmy jsou nezbytné pro použití statistických technik, pojďme se podívat:
Populace
Ve statistickém kontextu se populace týká vesmíru nebo skupiny, ze které informace pochází.
Nejsou vždy o lidech, protože to mohou být skupiny zvířat, rostlin nebo předmětů, jako jsou auta, atomy, molekuly, a dokonce i události a nápady..
Ukázat
Pokud je populace velmi velká, je z ní odebrán reprezentativní vzorek a analyzován bez ztráty příslušných informací..
Může být vybrán náhodně nebo podle některých kritérií dříve stanovených analytikem. Výhodou je, že je podmnožinou populace, je mnohem lépe zvládnutelná.
Variabilní
Odkazuje na soubor hodnot, které může určitá charakteristika populace nabývat. Studie může obsahovat několik proměnných, jako je věk, pohlaví, váha, akademická úroveň, rodinný stav, příjem, teplota, barva, čas a mnoho dalších.
Proměnné mohou mít různou povahu, takže existují kritéria pro jejich klasifikaci a poskytnutí nejvhodnějšího zacházení.
Kategorické proměnné a numerické proměnné
V závislosti na způsobu, jakým jsou měřeny, mohou být proměnné:
-Kategorický
-Numerické
Kategorické proměnné, nazývané také kvalitativní, představují vlastnosti, jako je rodinný stav osoby, který může být svobodný, ženatý, rozvedený nebo ovdovělý.
Místo toho číselné proměnné nebo kvantitativní, lze měřit, například věk, čas, hmotnost, příjem a další.
Diskrétní proměnné a spojité proměnné
Diskrétní proměnné berou pouze diskrétní hodnoty, jak naznačuje jejich název. Příkladem je počet dětí v rodině, počet předmětů v určitém kurzu a počet aut na parkovišti.
Tyto proměnné neberou vždy celočíselné hodnoty, protože existují i zlomkové.
Na druhé straně spojité proměnné připouštějí nekonečné hodnoty v určitém rozmezí, jako je hmotnost člověka, pH krve, doba telefonické konzultace a průměr fotbalových míčů..
Opatření centrální tendence
Poskytují představu o obecném trendu následovaném údaji. Uvedeme tři nejpoužívanější centrální opatření:
-Polovina
-Medián
-móda
Polovina
Ekvivalent k průměru hodnot. Vypočítává se sečtením všech pozorování a vydělením celkovým počtem:

móda
Je to hodnota, která se v datové sadě opakuje nejčastěji, nejčastěji nebo nejčastěji, protože v distribuci může existovat více než jeden režim.
Medián
Při třídění sady dat je střední hodnota centrální hodnotou všech z nich.
Míra disperze
Poukazují na variabilitu dat a poskytují představu o tom, jak daleko nebo rozptýleny jsou od centrálních opatření. Nejpoužívanější jsou:
Hodnost
Je to rozdíl mezi největší hodnotou xM a nejmenší xm ze souboru dat:
Pořadí = xM - Xm
Rozptyl
Měří, jak daleko jsou data od průměrné hodnoty. K tomu se vytvoří průměr, ale s rozdíly mezi jakoukoli hodnotou xi a průměr, kvadratura, aby se zabránilo jejich vzájemnému rušení. Obvykle se označuje řeckým písmenem σ na druhou nebo sdva:

Rozptyl nemá stejné jednotky jako data, takže standardní odchylka je definována jako druhá odmocnina rozptylu a je označena jako σ nebo s:

Místo toho, aby se jednotlivá data brala v úvahu, je lepší je seskupit do rozsahů, což usnadňuje práci, zejména pokud existuje mnoho hodnot. Například při práci s dětmi ve škole je lze rozdělit do věkových skupin: 0 až 6 let, 6 až 12 let a 12 až 18 let.
Grafy
Jsou skvělým způsobem, jak vidět distribuci dat na první pohled, a obsahují všechny informace shromážděné v tabulkách a tabulkách, ale mnohem dostupnější.
Existuje celá řada z nich: s pruhy, lineární, kruhové, stopkové a listové, histogramy, frekvenční polygony a piktogramy. Příklady statistických grafů jsou uvedeny na obrázku 3..
Témata zájmu
Větve statistik.
Statistické proměnné.
Populace a vzorek.
Inferenční statistiky.
Reference
- Faraldo, P. Statistika a metodologie výzkumu. Obnoveno z: eio.usc.es.
- Fernández, S. 2002. Popisné statistiky. 2. místo Edice. ESIC Editorial. Obnoveno z: Knihy Google.
- Historie statistik. Obnoveno z: eumed.net.
- Ibañez, P. 2010. Matematika II. Kompetenční přístup. Cengage Learning.
- Monroy, S. 2008. Popisné statistiky. 1. místo Edice. Národní polytechnický institut v Mexiku.
- Vesmírné vzorce. Deskriptivní statistika. Obnoveno z: universoformulas.com.



Zatím žádné komentáře