
Historie inferenční statistiky, charakteristiky, k čemu slouží, příklady

The inferenční statistiky nebo deduktivní statistika je statistika odvozující charakteristiky populace ze vzorků odebraných z ní pomocí řady analytických technik. Se získanými informacemi jsou vyvinuty modely, které poté umožňují předpovídat chování uvedené populace..
Z tohoto důvodu se inferenční statistika stala vědou číslo jedna v nabídce podpory a nástrojů, které při rozhodování vyžaduje nespočet oborů..

Fyzika, chemie, biologie, inženýrství a společenské vědy z těchto nástrojů neustále těží, když vytvářejí své modely a navrhují a provádějí experimenty..
Rejstřík článků
- 1 Stručná historie inferenční statistiky
- 1.1 Římská říše
- 1.2 Středověk
- 1.3 Moderní doba
- 1.4 Současná doba
- 2 Funkce
- 3 K čemu slouží popisná statistika? Aplikace
- 3.1 Sociologie a demografické studie
- 3.2 Inženýrství
- 3.3 Ekonomika a správa podniku
- 4 Příklady inferenční statistiky
- 4.1 Příklad 1
- 4.2 Příklad 2
- 5 základních pojmů v inferenční statistice
- 5.1 Událost
- 5.2 Ukázkový prostor
- 5.3 Populace a vzorek
- 5.4 Odběr vzorků
- 5.5 Statistické proměnné
- 5.6 Rozdělení pravděpodobnosti
- 5.7 Parametry a statistiky
- 5.8 Statistická hypotéza
- 5.9 Testy hypotéz
- 6 Témata zájmu
- 7 Reference
Stručná historie inferenčních statistik
Statistiky vznikly ve starověku kvůli potřebě lidí organizovat věci a optimalizovat zdroje. Před vynálezem psaní byly vedeny záznamy o počtu lidí a dostupných hospodářských zvířat pomocí symbolů, které byly vyryty do kamene..
Později čínští, babylonští a egyptští panovníci nechali na hliněných tabulkách, sloupech a pomnících vyryto údaje o množství plodin a počtu obyvatel..
Římská říše
Když Řím vykonával svou nadvládu ve Středomoří, bylo běžné, že úřady prováděly sčítání každých pět let. Slovo „statistika“ ve skutečnosti pochází z italského slova statistik, co to znamená vyjádřit.
Zároveň v Americe podobné záznamy vedly i velké předkolumbovské říše.
Středověk
Během středověku si evropské vlády i církev zaregistrovaly vlastnictví půdy. Totéž udělali při narození, křtu, sňatku a smrti.
Moderní doba
Anglický statistik John Graunt (1620-1674) jako první provedl předpovědi na základě takových seznamů, jako je například to, kolik lidí může zemřít na určité nemoci a odhadovaný podíl narozených mužů a žen. Z tohoto důvodu je považován za otce demografie..
Současná doba
Později, s příchodem teorie pravděpodobnosti, statistiky přestaly být pouhou sbírkou organizačních technik a dosáhly netušeného rozsahu jako prediktivní vědy..
Odborníci tak mohli začít vyvíjet modely chování populací a spolu s nimi odvodit, jaké věci se mohou stát lidem, předmětům a dokonce i myšlenkám.
Vlastnosti

Níže uvádíme nejdůležitější vlastnosti této oblasti statistiky:
- Inferenční statistiky studují populaci, která z ní odebírá reprezentativní vzorek.
- Výběr vzorku se provádí různými postupy, nejvhodnější jsou ty, které náhodně vybírají komponenty. Jakýkoli prvek populace má tedy stejnou pravděpodobnost, že bude vybrán, a tak se zamezí nechtěným předsudkům..
- K uspořádání shromážděných informací se využívá popisných statistik.
- Statistické proměnné se počítají na vzorku, který se používá k odhadu vlastností populace..
- Inferenční nebo deduktivní statistika využívá ke studiu náhodných událostí teorii pravděpodobnosti, tedy ty, které vznikají náhodně. Každá událost má přiřazenu určitou pravděpodobnost výskytu.
- Vytváří hypotézy - předpoklady - o parametrech populace a porovnává je, aby zjistil, zda jsou správné nebo ne, a také vypočítá úroveň spolehlivosti odpovědi, to znamená, že nabízí míru chyb. První postup se nazývá testování hypotéz, zatímco míra chyby je interval spolehlivosti.
K čemu slouží popisná statistika? Aplikace

Studium celé populace může vyžadovat velké množství peněz, času a úsilí. Je lepší odebírat reprezentativní vzorky, které jsou mnohem lépe zvládnutelné, shromažďovat z nich data a vytvářet hypotézy nebo předpoklady o chování vzorků.
Jakmile jsou stanoveny hypotézy a je ověřena jejich platnost, výsledky se rozšíří na populaci a použijí se k rozhodování..
Pomáhají také vytvářet modely této populace a vytvářet projekce pro budoucnost. Proto je inferenční statistika velmi užitečnou vědou pro:
Sociologie a demografické studie
Toto jsou ideální oblasti použití, protože statistické techniky jsou aplikovány s myšlenkou zavedení různých modelů lidského chování. Něco, co je apriori poměrně komplikované, protože do něj zasahují četné proměnné.
V politice je v době voleb široce používáno znát volební tendenci voličů, takto strany navrhují strategie.
inženýrství
Metody inferenčních statistik jsou v Engineering široce používány, nejdůležitějšími aplikacemi jsou kontrola kvality a optimalizace procesů, například zlepšování časů při provádění úkolů a prevence pracovních úrazů..
Ekonomika a správa podniku
Pomocí deduktivních metod můžete provádět projekce o fungování společnosti, očekávané úrovni prodeje a také pomoci při rozhodování.
Jejich techniky lze například použít k odhadu, jaká bude reakce kupujících na nový produkt, který má být uveden na trh..
Slouží také k vyhodnocení toho, jak se mění konzumní návyky lidí, vzhledem k důležitým událostem, jako je epidemie COVID..
Příklady inferenční statistiky
Příklad 1
Jednoduchý problém deduktivní statistiky je následující: učitel matematiky má na univerzitě na starosti 5 sekcí elementární algebry a rozhodne se použít průměrné známky jen jeden jejích sekcí odhadnout průměr Všechno.

Další možností je odebrat vzorek z každé sekce, prostudovat její vlastnosti a rozšířit výsledky na všechny sekce..
Příklad 2
Vedoucí obchodu s dámským oblečením chce vědět, kolik určité blůzy prodá během letní sezóny. Za tímto účelem analyzuje prodej oděvu během prvních dvou týdnů sezóny a určuje tak trend..
Základní pojmy v inferenční statistice
Existuje několik klíčových konceptů, včetně těch, které vycházejí z teorie pravděpodobnosti, v nichž musíte mít jasno, abyste pochopili celý rozsah těchto technik. Některé z nich, jako populace a vzorek, jsme již zmínili v celém textu.
událost
Událost nebo událost je něco, co se stane a které může mít několik výsledků. Příkladem události může být otočení mince a existují dva možné výsledky: hlavy nebo ocasy.
Ukázkový prostor
Jedná se o soubor všech možných výsledků události.
Populace a vzorek
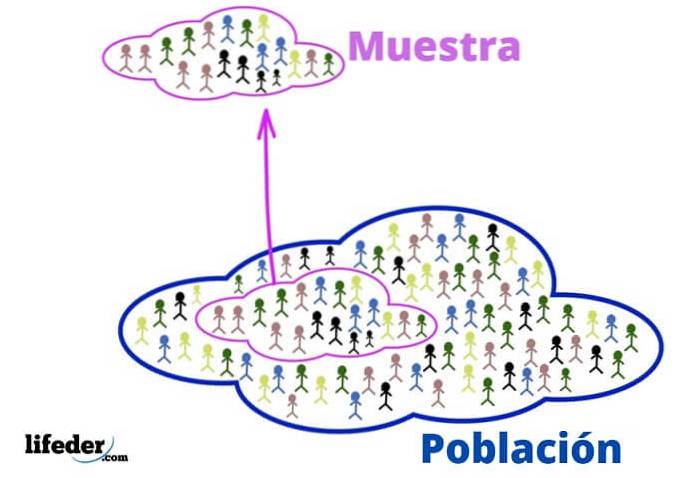
Populace je vesmír, který chcete studovat. Není to nutně o lidech nebo živých bytostech, protože populace se ve statistikách může skládat z předmětů nebo nápadů.
Vzorek je podmnožinou populace, která je z ní pečlivě extrahována, protože je reprezentativní..
Vzorkování
Jedná se o soubor technik, kterými je vzorek vybírán z dané populace. Vzorkování může být náhodné, pokud se k výběru vzorku použijí pravděpodobnostní metody, nebo nepravděpodobné, pokud má analytik podle svých zkušeností vlastní výběrová kritéria..
Statistické proměnné
Sada hodnot, které mohou mít charakteristiky populace. Jsou klasifikovány různými způsoby, například mohou být diskrétní nebo spojité. S přihlédnutím k jejich povaze mohou být také kvalitativní nebo kvantitativní..
Pravděpodobnostní rozdělení
Pravděpodobnostní funkce, které popisují chování velkého počtu systémů a situací pozorovaných v přírodě. Nejznámější jsou Gaussova nebo Gaussova distribuce zvonu a binomické rozdělení.
Parametry a statistiky
Teorie odhadu stanoví, že existuje vztah mezi hodnotami populace a hodnotami vzorku odebraného z této populace. The parametry jsou charakteristiky populace, které neznáme, ale chceme je odhadnout: například průměr a směrodatná odchylka.
Z jejich strany statistika jsou vlastnosti vzorku, například jeho průměr a směrodatná odchylka.
Jako příklad předpokládejme, že populaci tvoří všichni mladí lidé ve věku od 17 do 30 let v komunitě a chceme znát podíl těch, kteří v současné době mají vysokoškolské vzdělání. To by byl parametr populace k určení.
Pro jeho odhad je vybrán náhodný vzorek 50 mladých lidí a je vypočítán jejich podíl studující na univerzitě nebo vysokoškolském institutu. Tento podíl je statistický.
Pokud se po studii zjistí, že 63% z 50 mladých lidí má vysokoškolské vzdělání, jedná se o populační odhad ze vzorku.
Toto je jen jeden příklad toho, co mohou inferenční statistiky dělat. Je známý jako odhad, ale existují také techniky pro predikci statistických proměnných a pro rozhodování.
Statistická hypotéza
Jedná se o domněnku týkající se hodnoty průměru a směrodatné odchylky některé charakteristiky populace. Pokud není populace plně prozkoumána, jedná se o neznámé hodnoty.
Testování hypotéz
Jsou předpoklady o parametrech populace platné? Chcete-li zjistit, je ověřeno, zda je výsledky vzorku podporují, či nikoli, je tedy nutné navrhnout testy hypotéz.
Toto jsou obecné kroky k provedení jednoho:
Krok 1
Určete typ distribuce, kterou má populace následovat.
Krok 2
Uveďte dvě hypotézy, označené jako Hnebo a H1. První je nulová hypotéza ve kterém předpokládáme, že parametr má určitou hodnotu. Druhý je alternativní hypotéza který předpokládá jinou hodnotu než nulová hypotéza. Pokud je to odmítnuto, je přijata alternativní hypotéza.
Krok 3
Stanovte přijatelnou rezervu pro rozdíl mezi parametrem a statistikou. Zřídka se ukáží jako identické, i když se očekává, že budou velmi blízko..
Krok 4
Navrhněte kritérium pro přijetí nebo odmítnutí nulové hypotézy. K tomu se používá statistika testu, což může být průměr. Pokud je střední hodnota v určitých mezích, je přijata nulová hypotéza, jinak je odmítnuta.
Krok 5
Jako poslední krok se rozhodne, zda přijmeme nulovou hypotézu či nikoli..
Témata zájmu
Větve statistik.
Statistické proměnné.
Populace a vzorek.
Deskriptivní statistika.
Reference
- Berenson, M. 1985. Statistiky pro management a ekonomiku, koncepty a aplikace. Redakční Interamericana.
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage Learning.
- Historie statistik. Obnoveno z: eumed.net.
- Ibañez, P. 2010. Matematika II. Kompetenční přístup. Cengage Learning.
- Levin, R. 1981. Statistiky pro správce. Hala Prentice.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.


Zatím žádné komentáře