
Definice surjektivní funkce, vlastnosti, příklady
A surjektivní funkce je jakýkoli vztah, kde každý prvek patřící do codomainu je obrazem alespoň jednoho prvku domény. Také známý jako funkce na, jsou součástí klasifikace funkcí s ohledem na způsob, jakým jsou jejich prvky příbuzné.
Například funkce F: A → B definován F (x) = 2x
Který zní „F co takhle NA dokud B definován F (x) = 2x "
Je čas definovat počáteční a cílové sady A a B.
Odpověď: 1, 2, 3, 4, 5 Nyní hodnoty nebo obrázky, které každý z těchto prvků zobrazí při vyhodnocení F, budou prvky codomain.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Tak tvoří celek B: 2, 4, 6, 8, 10
Lze tedy dojít k závěru, že:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definován F (x) = 2x Je to surjektivní funkce
Každý prvek codomain musí být výsledkem alespoň jedné operace nezávislé proměnné prostřednictvím příslušné funkce. Neexistuje žádné omezení obrázků, prvek codomain může být obrazem více než jednoho prvku domény a stále se snaží jeden surjektivní funkce.
Obrázek ukazuje 2 příklady s surjektivní funkce.
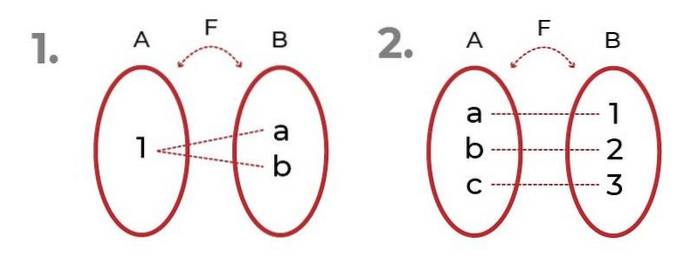
V první je pozorováno, že obrázky mohou být odkazovány na stejný prvek, aniž by byl ohrožen surjektivita funkce.
Ve druhém vidíme spravedlivé rozdělení mezi doménou a obrázky. To vede k bijektivní funkce, kde kritéria injektivní funkce a surjektivní funkce.
Další způsob identifikace surjektivní funkce, je zkontrolovat, zda se doména rovná rozsahu funkce. To znamená, že pokud je sada příchozích shodná s obrázky poskytnutými funkcí při hodnocení nezávislé proměnné, funkce je surjektivní.
Rejstřík článků
- 1 Vlastnosti
- 1.1 Podmínka funkce
- 2 Příklady: vyřešená cvičení
- 2.1 Cvičení 1
- 2.2 Cvičení 2
- 2.3 Cvičení 3
- 2.4 Cvičení 4
- 2.5 Cvičení 4
- 2.6 Cvičení 5
- 3 Navrhovaná cvičení
- 4 Odkazy
Vlastnosti
Zvážit surjektivní k funkci musí být splněno následující:
Být F: DF → CF
∀ b ℮ CF A do ℮ DF / F (a) = b
Toto je algebraický způsob, jak to dokázat pro všechna „b“, která patří CF existuje „a“, které patří D.F tak, že funkce F vyhodnocená v „a“ se rovná „b“.
Surjectivity je zvláštnost funkcí, kde codomain a rozsah jsou podobné. Prvky vyhodnocené ve funkci tedy tvoří sadu příchodů.
Podmínka funkce
Někdy funkce, která není surjektivní, může být vystaven určitým podmínkám. Tyto nové podmínky mohou způsobit, že surjektivní funkce.
Platí všechny druhy úprav domény a codomain funkce, kde cílem je splnit vlastnosti surjectivity v odpovídajícím vztahu.
Příklady: vyřešená cvičení
Splnit podmínky surjektivita musí být použity různé techniky úpravy, aby bylo zajištěno, že každý prvek codomain je v sadě obrazů funkce.
Cvičení 1
- Nechte funkci F: R → R definovaný řádkem F (x) = 8 - x
A: [All real numbers]
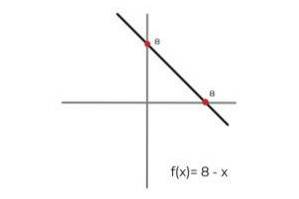
V tomto případě funkce popisuje spojitou čáru, která pokrývá všechna reálná čísla v doméně i rozsahu. Protože rozsah funkce RF rovná se codomain R Lze vyvodit závěr, že:
F: R → R definovaný řádkem F (x) = 8 - x je surjektivní funkce.
To platí pro všechny lineární funkce (funkce, jejichž největší stupeň proměnné je jedna).
Cvičení 2
- Prostudujte funkci F: R → R definován F (x) = xdva : Určete, zda se jedná o a surjektivní funkce. Pokud ne, uveďte podmínky nezbytné k tomu, aby to bylo surjektivní.
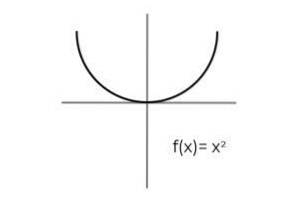
První věc, kterou je třeba zvážit, je codomain F, který se skládá ze skutečných čísel R. Funkce nemůže vrátit záporné hodnoty, což vylučuje skutečné negativy z možných obrázků.
Upravení domény na interval [0 , ∞ ]. Je vyloučeno, aby prvky komodity byly vzájemně nesouvisející F.
Obrázky se opakují pro dvojice prvků nezávislé proměnné, jako např x = 1 Y x = - 1. Ovlivňuje to však pouze injekčnost funkce, což pro tuto studii není problém.
Tímto způsobem lze dojít k závěru, že:
F: R →[0, ∞ ) definován F (x) = xdva Je to surjektivní funkce
Cvičení 3
- Definujte podmínky codomain, které budou dělat surjektivy k funkcím
F: R → R definován F (x) = Sen (x)
F: R → R definován F (x) = Cos (x)
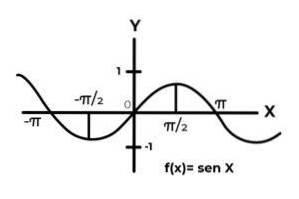
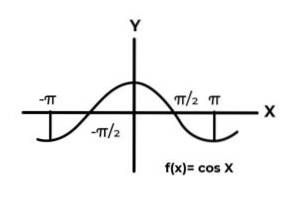
Chování trigonometrických funkcí je podobné chování vln, přičemž je velmi běžné najít mezi obrázky opakování závislé proměnné. Ve většině případů je také rozsah funkce omezen na jeden nebo více sektorů skutečné linie.
To je případ funkcí Sine a Cosine. Kde jejich hodnoty kolísají v intervalu [-1, 1]. Tento interval musí podmínit doménu, aby se dosáhlo surjektivity funkce.
F: R →[-elven] definován F (x) = Sen (x) Je to surjektivní funkce
F: R →[-elven]definován F (x) = Cos (x) Je to surjektivní funkce
Cvičení 4
- Prostudujte funkci
F: [0, ∞ ) → R definován F (x) = ± √x označte, zda se jedná o a surjektivní funkce
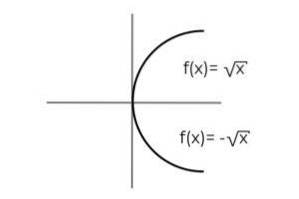
Funkce F (x) = ± √x Má tu zvláštnost, že definuje 2 závislé proměnné pro každou hodnotu „x“. To znamená, že rozsah přijímá 2 prvky pro každý vyrobený v doméně. Kladná a záporná hodnota musí být ověřena pro každou hodnotu „x“.
Při pozorování počáteční množiny je třeba poznamenat, že doména již byla omezena, aby se zabránilo indeterminacies vytvořené při hodnocení záporného čísla v sudém kořenu.
Při ověřování rozsahu funkce je třeba poznamenat, že každá hodnota codomainu patří do rozsahu.
Tímto způsobem lze dojít k závěru, že:
F: [0, ∞ ) → R definován F (x) = ± √x Je to surjektivní funkce
Cvičení 4
- Prostudujte funkci F (x) = Ln x označte, zda se jedná o a surjektivní funkce. Podmínkou sady příletu a odletu je přizpůsobení funkce kritériím surjektivity.
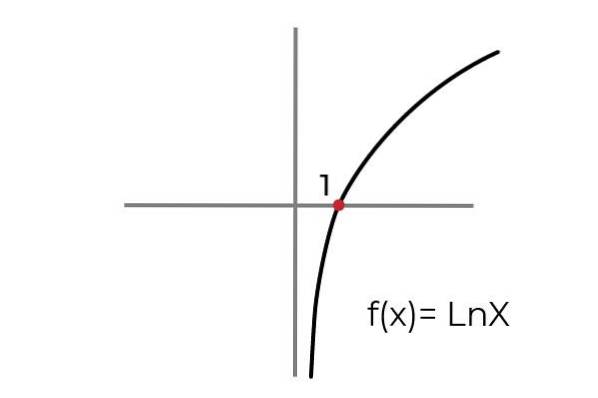
Jak ukazuje graf, funkce F (x) = Ln xje definován pro hodnoty "x" větší než nula. Zatímco hodnoty „a“ nebo obrázky mohou nabývat skutečné hodnoty.
Tímto způsobem můžeme omezit doménu F (x) = do intervalu (0 , ∞ )
Dokud lze rozsah funkce zachovat jako množinu reálných čísel R.
Vzhledem k tomu lze vyvodit závěr, že:
F: [0, ∞ ) → R definován F (x) = Ln x Je to surjektivní funkce
Cvičení 5
- Prozkoumejte funkci absolutní hodnoty F (x) = | x | a určit sady příletů a odletů, které splňují kritéria surjectivity.
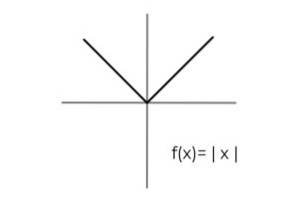
Doména funkce platí pro všechna reálná čísla R. Tímto způsobem musí být v doméně provedeno jediné kondicionování, přičemž se vezme v úvahu, že funkce absolutní hodnoty má pouze kladné hodnoty..
Pokračujeme ve stanovení codomainu funkce, která ji přirovná k hodnosti stejné
[0 , ∞ )
Nyní lze dojít k závěru, že:
F: [0, ∞ ) → R definován F (x) = | x | Je to surjektivní funkce
Navrhovaná cvičení
- Zkontrolujte, zda jsou následující funkce surjektivní:
- F: (0, ∞ ) → R definován F (x) = Log (x + 1)
- F: R → R definován F (x) = x3
- F: R →[1, ∞ ) definován F (x) = xdva + 1
- [0, ∞ ) → R definován F (x) = Log (2x + 3)
- F: R → R definován F (x) = Sec x
- F: R - 0 → R definován F (x) = 1 / x
Reference
- Úvod do logiky a kritického myšlení. Merrilee H. Salmon. University of Pittsburgh
- Problémy v matematické analýze. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polsko.
- Prvky abstraktní analýzy. Mícheál O'Searcoid PhD. Katedra matematiky. University College Dublin, Beldfield, Dublind 4
- Úvod do logiky a metodologie dedukčních věd. Alfred Tarski, New York Oxford. Oxford University Press.
- Principy matematické analýzy. Enrique Linés Escardó. Redakční Reverté S. A 1991. Barcelona Španělsko.


Zatím žádné komentáře