Vzorce magnetické indukce, způsob výpočtu a příklady

The magnetická indukce nebo hustota magnetického toku je změna prostředí způsobená přítomností elektrických proudů. Upravují povahu prostoru, který je obklopuje, a vytvářejí a venkov vektor.

Vektor magnetická indukce, hustota magnetického toku Nebo jednoduše magnetické pole B, má tři charakteristické vlastnosti: intenzitu vyjádřenou číselnou hodnotou, směr a také smysl daný v každém bodě vesmíru. Je zvýrazněn tučně, aby se odlišil od čistě číselných nebo skalárních veličin.

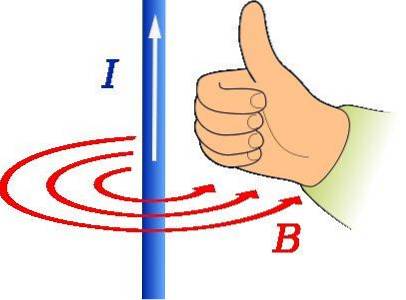
Pravidlo pravého palce se používá k nalezení směru a směru magnetického pole způsobeného vodičem pro vedení proudu, jak je znázorněno na obrázku výše.

Palec pravé ruky by měl směřovat ve směru proudu. Poté rotace čtyř zbývajících prstů označuje tvar B, který je na obrázku reprezentován soustřednými červenými kruhy.

V takovém případě adresa B je tangenciální k obvodu soustředné s drátem a je proti směru hodinových ručiček.

The magnetická indukce B V mezinárodním systému se měří Tesla (T), ale častěji se měří v jiné jednotce zvané Gauss (G). Obě jednotky byly pojmenovány na počest Nikoly Tesly (1856-1943) a Carla Friedricha Gaussa (1777-1855) za mimořádný přínos v oblasti vědy o elektřině a magnetismu..

Rejstřík článků

• 1 Jaké jsou vlastnosti magnetické indukce nebo hustoty magnetického toku?
• 2 Biot-Savartův zákon
• 3 vzorce
• 4 Jak se počítá?
  • 4.1 Příklad
• 5 Reference

Jaké jsou vlastnosti magnetické indukce nebo hustoty magnetického toku?

Kompas umístěný v blízkosti živého drátu se vždy zarovná s B. Dánský fyzik Hans Christian Oersted (1777-1851) si tento fenomén všiml jako první na počátku 19. století.

A když proud ustane, kompas opět jako vždy ukazuje na zeměpisný sever. Pečlivou změnou polohy kompasu se získá mapa tvaru magnetického pole.

Tato mapa má vždy tvar kruhů soustředných s drátem, jak je popsáno na začátku. Tímto způsobem si můžete vizualizovat B.

I v případě, že drát není rovný, vektor B vytvoří kolem něj soustředné kruhy. Chcete-li určit tvar pole, představte si velmi malé segmenty drátu, tak malé, že vypadají jako přímočaré a obklopené soustřednými kruhy..

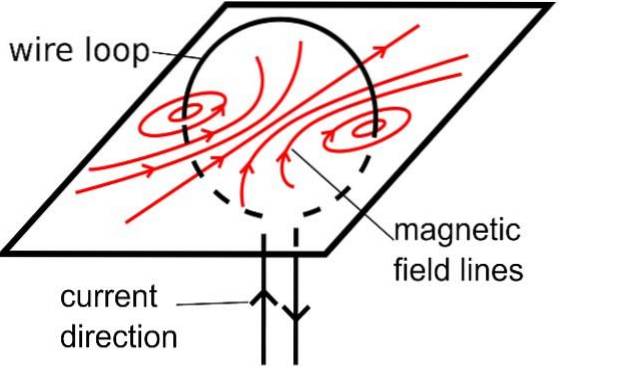
To ukazuje na důležitou vlastnost čar magnetického pole. B: nemají začátek ani konec, jsou to vždy uzavřené křivky.

Biot-Savartův zákon

19. století znamenalo začátek věku elektřiny a magnetismu ve vědě. Kolem roku 1820 francouzští fyzici Jean Marie Biot (1774-1862) a Felix Savart (1791-1841) objevili zákon, který nese jejich jméno a který nám umožňuje vypočítat vektor B.

Provedli následující pozorování o příspěvku k magnetickému poli produkovanému segmentem drátu o diferenciální délce dl který nese elektrický proud Já:

• Velikost B klesá s inverzním čtvercem vzdálenosti od drátu (to dává smysl: od drátu intenzita B musí být menší než blízké body).
• Velikost B je úměrná intenzitě proudu Já který prochází drátem.
• Adresa B je tangenciální k obvodu poloměru r soustředěný na drát a smysl pro B je dáno, jak jsme řekli, pravidlem pravého palce.

Křížový součin nebo křížový součin je vhodný matematický nástroj k vyjádření posledního bodu. K vytvoření vektorového produktu jsou zapotřebí dva vektory, které jsou definovány takto:

• dl je vektor, jehož velikost je délka diferenciálního segmentu dl
• r je vektor, který vede z drátu do bodu, kde chcete najít pole

Vzorce

To vše lze spojit do matematického výrazu:

Konstanta proporcionality nezbytná pro nastolení rovnosti je magnetická permeabilita volného prostoru μ_nebo  = 4π.10^-7 T.m / A

Tímto výrazem je Biotův a Savartův zákon, který nám umožňuje vypočítat magnetické pole aktuálního segmentu.

Takový segment zase musí být součástí většího a uzavřenějšího obvodu: distribuce proudu.

Podmínka, že je obvod uzavřen, je nutná pro tok elektrického proudu. V otevřených obvodech nemůže proudit elektrický proud.

Nakonec, aby se zjistilo celkové magnetické pole uvedeného rozdělení proudu, sečtou se všechny příspěvky každého diferenciálního segmentu dl. To odpovídá integraci v celé distribuci:

Chcete-li použít zákon Biot-Savart a vypočítat vektor magnetické indukce, je nutné vzít v úvahu několik velmi důležitých důležitých bodů:

• Křížový produkt mezi dvěma vektory má vždy za následek jiný vektor.

• 

• Je vhodné najít vektorový produkt před přejít na rozlišení integrálu, pak je vyřešen integrál každé ze složek získaných samostatně.
• Je nutné vykreslit situaci a vytvořit vhodný souřadnicový systém.
• Kdykoli je pozorována existence nějaké symetrie, měla by být použita k úspoře času výpočtu.
• Pokud existují trojúhelníky, Pythagorova věta a kosinová věta jsou velkou pomocí k vytvoření geometrického vztahu mezi proměnnými.

Jak se to počítá?

S praktickým příkladem výpočtu B pro přímý vodič platí tato doporučení.

Příklad

Vypočítejte vektor magnetického pole, který vytváří velmi dlouhý přímočarý drát v bodě P v prostoru, podle zobrazeného obrázku.

Z obrázku musíte:

• Drát je směrován ve svislém směru, přičemž proud I proudí nahoru. Tento směr je + y v souřadnicovém systému, jehož počátek je v bodě O.

• 

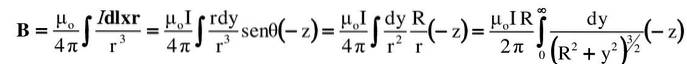
• V takovém případě podle pravidla pravého palce, B v bodě P je směrován dovnitř papíru, proto je označen malým kroužkem a „x“ na obrázku. Tato adresa bude brána jako -z.
• Pravý trojúhelník, jehož nohy jsou Y Y R, vztahují obě proměnné podle Pythagorovy věty: r^dva= R.^dva+Y^dva

To vše je v integrálu nahrazeno. Křížový produkt nebo kříž je označen svou velikostí plus svým směrem a smyslem:

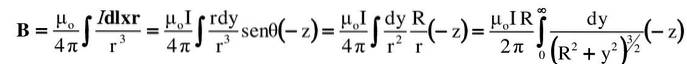
Navrhovaný integrál se nachází v tabulce integrálů nebo je řešen vhodnou trigonometrickou substitucí (výsledek si může čtenář ověřit pomocí y = Rtg θ):

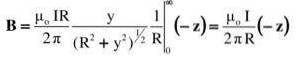
Výsledek souhlasí s tím, co se očekávalo: velikost pole klesá se vzdáleností R a úměrně se zvyšuje s intenzitou proudu I.

Ačkoli nekonečně dlouhý drát je idealizace, získaný výraz je velmi dobrou aproximací pro pole dlouhého drátu.

S Biotovým a Savartovým zákonem je možné najít magnetické pole jiných vysoce symetrických distribucí, jako je kruhová smyčka, která nese proud, nebo ohnuté dráty kombinující přímočaré a křivočaré segmenty..

Samozřejmě, aby bylo možné analyticky vyřešit navrhovaný integrál, musí mít problém vysoký stupeň symetrie. Jinak je alternativou řešení numerického integrálu.

Reference

1. Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 2. Mexiko. Cengage Learning Editors. 367-372.