
Grashofovy právní případy, mechanismy, příklady, aplikace
The Grashofův zákon tvrdí, že: V plochém mechanismu se čtyřmi kloubovými tyčemi, přičemž jedna z nich je pevná, může alespoň jedna z tyčí provést úplnou zatáčku za předpokladu, že součet nejkratší tyče a nejdelší tyče je menší nebo roven součtu ostatních dvou.
Existuje pět plochých čtyřbarevných nebo spojovacích mechanismů, které jsou v souladu s Grashofovým zákonem (Příklad je uveden na obrázku 1). Aby se tyče nebo články mechanismů, které jsou v souladu se zákonem, mohly úplně otočit, je nutné, aby ve skutečném uspořádání každá tyč zabírala různé paralelní roviny.
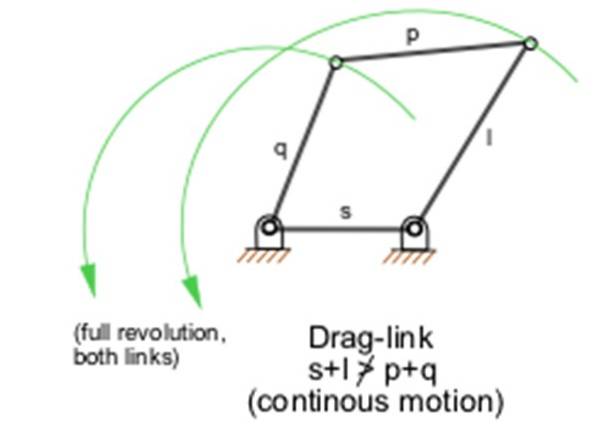
Grashofův zákon je jednoduché pravidlo, které vám umožňuje navrhnout mechanismus, který vyžaduje plnou rotaci, buď proto, že bude připojen motor, nebo naopak, protože chcete transformovat oscilační pohyb na rotační, a to takovým způsobem, že je matematický a fyzicky životaschopný.
Rejstřík článků
- 1 Hraniční případy
- 1.1 Druhy pohybu
- 2 Mechanismy, které jsou v souladu se zákonem Grashof
- 2.1 - Mechanismus dvojité kliky
- 2.2 - Více mechanismů, které jsou v souladu se zákonem Grashof
- 3 Aplikace
- 3.1 Mechanismus klikové houpačky
- 3.2 Mechanismus kloubového rovnoběžníku
- 3.3 Kloubový mechanismus proti paralelogramu
- 4 Odkazy
Hraniční případy
Předpokládejme, že čtyři spojovací pruhy mají následující délky seřazené od nejmenší po největší podle:
s> p> q> l
Grashofův zákon stanoví, že alespoň u jednoho pruhu nebo odkazu k dokončení revoluce nebo obratu musí být splněna podmínka:
s + l <= p + q
Tato nerovnost má následující důsledky:
- Jediným pruhem nebo článkem, který může poskytnout plné otáčky vůči druhému, je nejkratší pruh.
- Pokud se kratší pruh dostane do plných otáček vzhledem k druhému, provede také plné otáčky vzhledem ke všem ostatním.
Druhy pohybu
Pohyb kloubového čtyřúhelníku, který je v souladu s Grashofovým zákonem, může být následujících typů:
- Dvojitým otočením nebo klikou, pokud je nejkratší tyč pevná a sousední tyče provedou úplné zatáčky.
- Tam a zpět, pokud krátká lišta sousedí s pevnou lištou.
- Double rocker, pokud je nejkratší lišta naproti pevné.
Když je rovnost splněna ve vzorci Grashof, pak jsme v omezujícím případě, kdy se součet nejkratší lišty s nejdelší lištou rovná součtu ostatních dvou.
V tomto případě může mechanismus nabrat konfiguraci, ve které jsou čtyři pruhy zarovnány. A v této poloze mohou nefixované klouby lhostejně jít tak či onak, což způsobí zablokování mechanismu..
Mechanismy, které splňují podmínku Grashof, jsou spolehlivější a méně trpí na své klouby a vazby, pokud jsou dále od omezujícího případu rovnosti.
Mechanismy, které jsou v souladu se zákonem Grashof
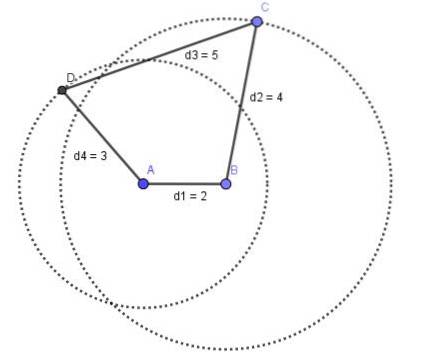
Označíme po sobě jdoucí klouby A, B, C a D, poté:
- A a B jsou pevné čepy.
- AB = d1 (pevná lišta)
- BC = d2
- CD = d3
- DA = d4
- Mechanismus dvojité kliky
Tyče b2 a b4 se zcela otáčejí a Grashofův zákon je splněn:
d1 + d3 <= d2+d4.
- Více mechanismů, které jsou v souladu se zákonem Grashof
Vlastnosti dalších mechanismů, které jsou v souladu se zákonem Grashof, jsou pojmenovány a popsány níže:
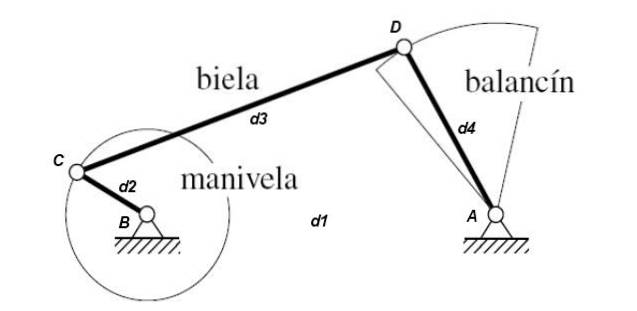
Klikový mechanismus - kolébkový
D2 + d3 je splněno <= d1 + d4
Kratší tyč d2 se plně otáčí a protilehlá tyč d4 provádí kolébkový pohyb.
Zdvojený kolébkový mechanismus
- Pevná lišta AB je větší než lišta opačné lišty CD a splňuje to:
d1 + d3 <= d2 + d3
- U kratší tyče (opak pevné tyče) je schopna provést celou zatáčku.
Kloubový mechanismus rovnoběžníku
- Tyče AD a BC jsou stejně dlouhé a vždy rovnoběžné.
- Na druhou stranu jsou lišty AB a CD stejně dlouhé a vždy rovnoběžné.
- V případě protilehlých tyčí mají stejnou délku a d1 + d2 = d3 + d4 je splněn podle zákona Grashof.
- Nakonec se tyče AD a BC otočí úplně stejným směrem.
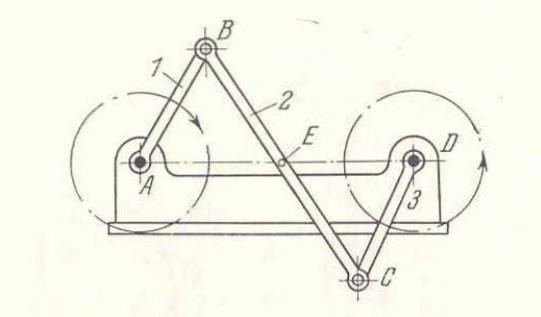
Kloubový anti-paralelogram
- Tyče AD a BC jsou stejně dlouhé a nejsou rovnoběžné.
- U tyčí AB a CD musí mít stejnou délku a nesmí být rovnoběžné.
- Na druhé straně mají protilehlé pruhy stejnou délku, dvě z nich jsou zkřížené.
- V tomto mechanismu musí být splněna následující podmínka:
d1 + d2 = d3 + d4
- Otočení tyčí AD a BC je úplné, ale v opačných směrech.
Aplikace
Mechanismy, které splňují zákon Grashof, mají několik aplikací:
Crank Mechanism - Rocker
Aplikuje se na šicí stroj na pedály, což je užitečné v místech, kde není elektrická energie, ve kterých pedál provádí kývavý nebo kývavý pohyb, který se přenáší na kolo spojené kladkou se šicím strojem.
Dalším příkladem, který je třeba zmínit, je mechanismus stěrače čelního skla. V tomto případě je k klikové tyči připojen motor, který provádí úplné zatáčky a přenáší kolébkový pohyb na tyč, která pohybuje prvním kartáčem systému..
Další aplikací klikového mechanismu jsou vahadla pro čerpání oleje ze země.

K klikě je připojen motor, který se zcela otáčí a přenáší pohyb na čerpací hlavu nebo vahadlo..
Kloubový mechanismus rovnoběžníku
Tento mechanismus se dříve používal pro spojování kol parních lokomotiv, takže se obě kola otáčí stejným směrem a stejnou rychlostí..
Hlavní charakteristikou tohoto mechanismu je, že tyč, která spojuje obě kola, má stejnou délku jako oddělení jejich náprav..
Pantograf je kreslicí nástroj používaný ke kopírování a zvětšování obrázků. Je založen na čtyřtaktovém mechanismu, ve kterém jsou čtyři klouby, které tvoří vrcholy rovnoběžníku..
Kloubový mechanismus proti paralelogramu
Jedná se o mechanismus používaný ve vrhacím stroji na tenisový míček, kde se musí kola, která pohánějí a odpalují míč, otáčet v opačných směrech..
Reference
- Clemente C. Virtuální laboratoř klikového mechanismu. Diplomová práce ve strojírenství. University of Almería. (2014). Obnoveno z: repositorio.ual.es
- Zákon Hurtada F. Grashofa. Obnoveno z: youtube.com
- Mech Designer. Kritérium Kinematics Grashof. Obnoveno z: mechdesigner.support.
- Shigley, J. Teorie strojů a mechanismů. Mc-Graw Hill.
- Jsme F1. Analýza mechanismu čtyř pruhů. Obnoveno z: youtube.com
- UNAM. Vývoj čtyřtaktního mechanismu pro použití ve výuce. Obnoveno z: ptolomeo.unam.mx
- Wikipedia. Vazba čtyř tyčí. Obnoveno z: en.wikipedia.com
- Wikipedia. Grashofův zákon. Obnoveno z: es.wikipedia.com


Zatím žádné komentáře