
Vysvětlení Keplerových zákonů, cvičení, experiment
The Keplerovy zákony o planetárním pohybu formuloval německý astronom Johannes Kepler (1571-1630). Kepler je odvodil na základě práce svého učitele dánského astronoma Tycha Braheho (1546-1601).
Brahe pečlivě shromažďoval údaje o planetárních pohybech za více než 20 let s překvapivou přesností a přesností, vzhledem k tomu, že dalekohled v té době ještě nebyl vynalezen. Platnost vašich údajů platí dodnes.

Rejstřík článků
- 1 Keplerovy 3 zákony
- 2 Zákon univerzální gravitace a třetí Keplerův zákon
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 experiment
- 4.1 Materiály
- 4.2 Postup
- 5 Reference
Keplerovy 3 zákony
Keplerovy zákony stanoví:
-První zákon: všechny planety popisují eliptické dráhy se Sluncem v jednom z ohnisek.
-Druhý zákon nebo zákon stejných oblastí: čára směrovaná ze Slunce na jakoukoli planetu (ohniskový poloměr), zametá stejné oblasti ve stejných časech.
-Třetí zákon: čtverec času potřebného na oběžnou dráhu planety kolem Slunce je úměrný krychli jeho průměrné vzdálenosti od Slunce.
Být T řekl čas, zavolal oběžná doba, Y r průměrná vzdálenost, pak:
Tdva je úměrný r3
T = k r3
To znamená, že podíl Tdva/ r3 je stejný pro všechny planety, což umožňuje vypočítat oběžný poloměr, pokud je známa oběžná doba.
Když T je vyjádřena v letech a r v astronomických jednotkách AU * je konstanta proporcionality k = 1:
Tdva= r3
* Astronomická jednotka se rovná 150 milionům kilometrů, což je průměrná vzdálenost mezi Zemí a Sluncem. Oběžná doba Země je 1 rok.
Zákon univerzální gravitace a třetí Keplerův zákon
Univerzální gravitační zákon uvádí, že velikost gravitační síly přitažlivosti mezi dvěma objekty hmot M Y m jejichž středy jsou odděleny vzdáleností r, darováno:
F = G mM / rdva
G je univerzální gravitační konstanta a její hodnota je G = 6 674 x 10 -jedenáct N.mdva/ kgdva .
Oběžné dráhy planet jsou nyní eliptické s velmi malou excentricitou.
To znamená, že oběžná dráha není příliš daleko od obvodu, s výjimkou některých případů, jako je trpasličí planeta Pluto. Pokud aproximujeme oběžné dráhy na kruhový tvar, zrychlení pohybu planety je:
naC = vdva/ r
Vzhledem k F = ma, mít:
G mM / rdva = m.v.dva/ r
Tady proti je lineární rychlost planety kolem Slunce, předpokládaná statická a hmotná M, zatímco planeta je m. Pak:

To vysvětluje, že planety dále od Slunce mají nižší orbitální rychlost, protože to závisí na 1 / √r.
Vzhledem k tomu, že vzdálenost, kterou planeta urazí, je přibližně délka obvodu: L = 2πr a trvá čas rovný orbitální periodě T, získáme:
v = 2πr / T
Rovnice obou výrazů pro v dává platný výraz pro Tdva, čtverec orbitálního období:

A toto je přesně třetí Keplerův zákon, protože v tomto výrazu je závorka 4πdva / GM je proto konstantní Tdva je úměrná vzdálenosti r krychlový.
Definitivní rovnice pro oběžné období se získá druhou odmocninou:

Kolik stojí hmotnost Slunce? To je možné zjistit pomocí této rovnice. Víme, že oběžná doba Země je jeden rok a oběžný poloměr je 1 AU, což odpovídá 150 milionům kilometrů, takže máme všechna potřebná data.
V naší předchozí rovnici řešíme pro M, ne bez předchozího převodu všech hodnot do Mezinárodního systému jednotek SI:
1 rok = 3,16 x 107 sekundy.
1 AU = 150 milionů km = 1,5 x10jedenáct m.

Výcvik
Ačkoli Kepler měl při odvozování svých slavných zákonů na mysli pouze planety, jsou platné i pro pohyb satelitů a jiných těles sluneční soustavy, jak uvidíme níže..
- Cvičení 1
S vědomím, že oběžná dráha Jupitera je 5,19krát větší než oběžná dráha Země, najděte oběžnou dobu Jupitera.
Řešení
Podle definice Astronomické jednotky je Jupiter vzdálený od Slunce 5,19 AU, tedy podle třetího Keplerova zákona:
Tdva= r3= (5,19)3 let
Proto T = (5,19)3/2 let = 11,8 let
- Cvičení 2
Kometa Halley navštěvuje Slunce každých 75,3 let. Nalézt:
a) Poloviční hlavní osa jeho oběžné dráhy.
b) Míra afélií, pokud perihélium měří 0,568 AU.
Řešení
Kometa Halley navštěvuje Slunce každých 75,3 let. Nalézt:
a) Poloviční hlavní osa jeho oběžné dráhy.
b) Míra afélií, pokud perihélium měří 0,568 AU.
Řešení
Když je planeta nebo jakákoli jiná hvězda v nejbližším bodě ke Slunci, říká se, že je v přísluní, a když je dále, v afélium. Ve zvláštním případě kruhové oběžné dráhy je r ve třetím Keplerově zákoně poloměr oběžné dráhy.
Na eliptické oběžné dráze je však nebeské těleso víceméně daleko od Slunce, přičemž hlavní poloosa „a“ je průměr mezi aphelionem a perihelionem:

Proto ve třetím Keplerově zákoně dosadíme r za, což pro Halleyho znamená:
Tdva= a3→ a = (T)2/3 → a = (75,3) 2/3 UA = 17 832 UA
Řešení b
a = ½ (Perihelion + Aphelion)
17,832 = ½ (0,568+ Aphelion) → Aphelion = 2 x 17,832 - 0,568 AU = 35,10 AU.
Experiment
Analýza pohybu planet vyžaduje týdny, měsíce a dokonce roky pečlivého pozorování a zaznamenávání. Ale v laboratoři lze provést velmi jednoduchý experiment v měřítku, aby se prokázalo, že platí Keplerův zákon rovných oblastí..
K tomu je zapotřebí fyzický systém, ve kterém je síla, která řídí pohyb, ústřední, což je dostatečná podmínka pro splnění zákonů oblastí. Takový systém se skládá z hmoty vázané na dlouhé lano, přičemž druhý konec nitě je připevněn k podpěře..
Hmota se pohybuje ze své rovnovážné polohy o malý úhel a je jí dán mírný impuls, takže provádí oválný (téměř eliptický) pohyb v horizontální rovině, jako by to byla planeta kolem Slunce..
Na křivce popsané kyvadlem můžeme dokázat, že zametá stejné oblasti ve stejných časech, pokud:
-Uvažujeme vektorové poloměry, které jdou od středu přitažlivosti (počátečního bodu rovnováhy) k poloze hmoty.
-A zametáme mezi dvěma po sobě jdoucími instancemi se stejnou dobou trvání ve dvou různých oblastech pohybu.
Čím delší je struna kyvadla a čím menší je úhel od svislice, bude čistá obnovovací síla vodorovnější a simulace se podobá případu pohybu s centrální silou v rovině.
Poté se popsaný ovál přiblíží k elipsě, jako je ta, kterou planety cestují.
Materiály
-Neroztažitelná nit
-1 těsto nebo kovová koule natřená bílou barvou, která funguje jako kyvadlo
-Pravítko
-Dopravník
-Fotografická kamera s automatickým stroboskopickým diskem
-Závorky
-Dva světelné zdroje
-List černého papíru nebo lepenky
Proces
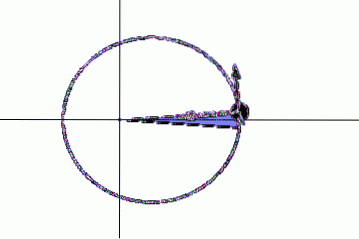
Sestavení obrázku je nutné pro pořízení fotografií několika záblesků kyvadla, které sleduje jeho dráhu. K tomu musíte umístit kameru těsně nad kyvadlo a automatický stroboskopický disk před objektiv.
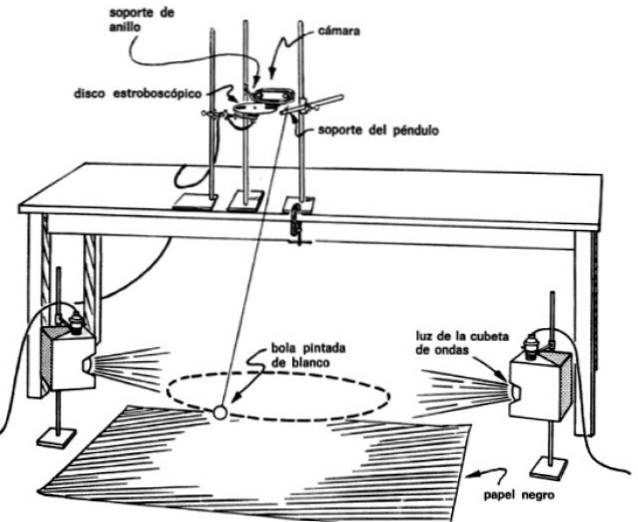
Tímto způsobem se získávají obrazy v pravidelných časových intervalech kyvadla, například každých 0,1 nebo každých 0,2 sekundy, což umožňuje zjistit čas potřebný k pohybu z jednoho bodu do druhého..
Musíte také správně osvětlit hmotu kyvadla a světla umístit na obě strany. Čočka by měla být natřena bílou barvou, aby se zlepšil kontrast pozadí, který se skládá z černého papíru na zemi.
Nyní musíte zkontrolovat, zda kyvadlo zametá stejné oblasti ve stejných časech. K tomu je zvolen časový interval a body obsazené kyvadlem v uvedeném intervalu jsou označeny na papíře..
Na obrázku je nakreslena čára od středu oválu k těmto bodům, a tak budeme mít první z oblastí zametených kyvadlem, což je přibližně eliptický sektor, jako je ten zobrazený níže:
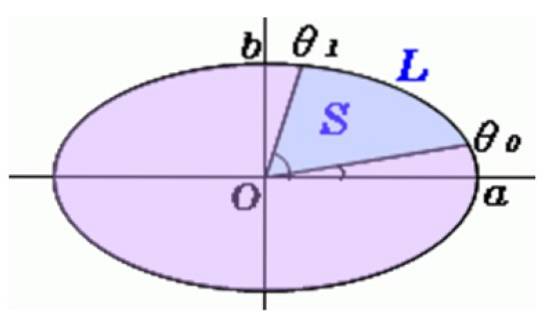
Výpočet plochy eliptického řezu
Úhly se měří úhloměrem θnebo Y θ1, a tento vzorec se používá k nalezení S, oblasti eliptického sektoru:
S = F (θ1) - F (θnebo)
S F (θ) dána:

Všimněte si, že na Y b jsou poloviční a vedlejší osy. Čtenář se musí starat pouze o pečlivé měření poloos a úhlů, protože online kalkulátory umožňují tento výraz snadno vyhodnotit..
Pokud však trváte na ručním výpočtu, nezapomeňte, že úhel θ se měří ve stupních, ale při zadávání dat do kalkulačky musí být hodnoty vyjádřeny v radiánech.
Poté musíte označit další dvojici bodů, ve kterých kyvadlo převrátilo stejný časový interval, a nakreslit příslušnou plochu, vypočítat její hodnotu stejným postupem.
Ověření práva rovných oblastí
Nakonec zbývá ověřit, zda je splněn zákon o oblastech, tj. Že stejné oblasti jsou zametány ve stejných časech.
Liší se výsledky trochu od toho, co se očekávalo? Vždy je třeba mít na paměti, že všechna měření jsou doprovázena příslušnou experimentální chybou.
Reference
- Keisan online kalkulačka. Oblast eliptické sektorové kalkulačky. Obnoveno z: keisan.casio.com.
- Openstax. Keplerův zákon planetárního pohybu. Obnoveno z: openstax.org.
- PSSC. Laboratorní fyzika. Redakční reverté. Obnoveno z: books.google.co.
- Palen, S. 2002. Astronomy. Série Schaum. Mcgraw kopec.
- Pérez R. Jednoduchý systém s centrální silou. Obnoveno z: francesphysics.blogspot.com
- Stern, D. Keplerovy tři zákony planetárního pohybu. Obnoveno z: phy6.org.


Zatím žádné komentáře