
Charakteristika kolmé přímky, příklady, cvičení
A kolmá čára Je to ten, který svírá úhel 90 ° vzhledem k jiné přímce, křivce nebo ploše. Všimněte si, že když jsou dvě čáry kolmé a jsou ve stejné rovině, když se protínají, tvoří čtyři stejné úhly, každá z nich má 90 °.
Pokud jeden z úhlů není 90 °, říká se, že čáry jsou šikmé. Svislé čáry jsou běžné v designu, architektuře a konstrukci, například síť potrubí na následujícím obrázku.

Orientace kolmých čar může být různá, například ty, které jsou uvedeny níže:
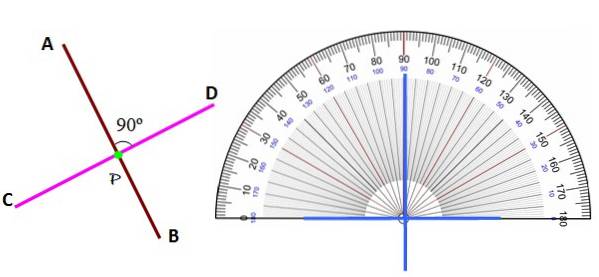
Bez ohledu na polohu jsou čáry navzájem kolmé rozpoznány podle úhlu mezi nimi jako 90 ° pomocí úhloměru.
Všimněte si, že na rozdíl od rovnoběžných čar v rovině, které se nikdy neprotínají, kolmé čáry to vždy dělají v bodě P, zvaném chodidlo jedné z čar nad druhou. Proto jsou také dvě kolmé čáry blottery.
Jakákoli přímka má nekonečné kolmice, protože pouhým pohybem segmentu AB doleva nebo doprava po segmentu CD budeme mít nové kolmice s další nohou.
Je však volána kolmice, která prochází středem segmentu půlení uvedeného segmentu.
Rejstřík článků
- 1 Příklady kolmých čar
- 1.1 Další příklady kolmých čar
- 2 Cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Příklady kolmých čar
Kolmé čáry jsou v městské krajině běžné. Na následujícím obrázku (obrázek 3) je zvýrazněno pouze několik z mnoha kolmých čar, které lze vidět na jednoduché fasádě této budovy a jejích prvků, jako jsou dveře, kanály, schody a další:

Dobrá věc je, že tři vzájemně na sebe kolmé čáry nám pomáhají určit polohu bodů a objektů v prostoru. Jsou to souřadnicové osy označené jako Osa X., Osa y Y osa z, jasně viditelné v rohu obdélníkové místnosti, jako je ta níže:
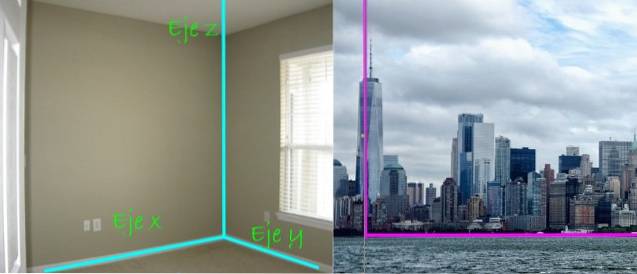
Na panoramatickém pohledu na město je vpravo také patrná kolmost mezi mrakodrapem a zemí. První, řekli bychom, se nachází podél osa z, zatímco země je rovina, což je v tomto případě rovina xy.
Pokud země tvoří rovinu xy, mrakodrap je také kolmý na jakoukoli cestu nebo ulici, což zaručuje jeho stabilitu, protože šikmá konstrukce je nestabilní.
A v ulicích, kdekoli jsou obdélníkové rohy, existují kolmé čáry. Mnoho ulic a ulic má kolmé rozložení, pokud to terén a geografické rysy umožňují..
Ke krátkému vyjádření kolmosti mezi čarami, segmenty nebo vektory se používá symbol ⊥. Například pokud je řádek L1 je kolmá na přímku Ldva, psali jsme:
L1 ⊥ L.dva
Další příklady kolmých čar
- V návrhu jsou kolmé čáry velmi přítomné, protože mnoho běžných objektů je založeno na čtvercích a obdélnících. Tyto čtyřúhelníky se vyznačují vnitřními úhly 90 °, protože jejich strany jsou rovnoběžné dvě po druhé:
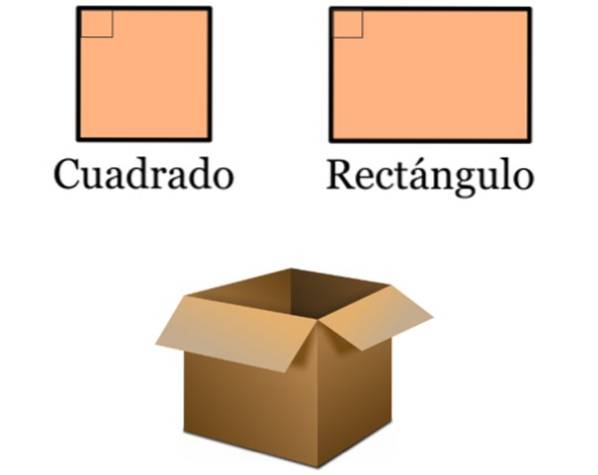
- Pole, ve kterých se cvičí různé sporty, jsou ohraničena četnými čtverci a obdélníky. Ty zase obsahují kolmé čáry.
- Dva ze segmentů, které tvoří pravý trojúhelník, jsou na sebe kolmé. Tito se nazývají nohy, zatímco je volán zbývající řádek přepona.
- Čáry vektoru elektrického pole jsou kolmé na povrch vodiče v elektrostatické rovnováze.
- U nabitého vodiče jsou ekvipotenciální vedení a povrchy vždy kolmé k elektrickému poli.
- V potrubních nebo potrubních systémech používaných k přepravě různých druhů tekutin, jako je plyn znázorněný na obrázku 1, jsou pravoúhlé lokty běžné. Proto tvoří kolmé čáry, jako je tomu v případě kotelny:

Výcvik
- Cvičení 1
Pomocí pravítka a kompasu nakreslete dvě kolmé čáry.
Řešení
Je to velmi jednoduché, postupujte podle těchto kroků:
-První čára je nakreslena, nazývá se AB (černá).
-Nahoře (nebo níže, pokud chcete) označte bod P, kterým projde kolmice. Pokud je P těsně nad (nebo pod) středem AB, je tato kolmice půlící částí segmentu AB.
-S kompasem soustředěným na P nakreslete kruh, který prořízne AB ve dvou bodech, nazývaných A 'a B' (červená).
-Kompas se otevře na A'P, je vycentrován na A 'a nakreslí se kruh, který prochází P (zelený).
-Opakujte předchozí krok, ale nyní otevřete míru délky segmentu B'P (zelená). Oba oblouky obvodu se protínají v bodě Q pod P a samozřejmě v druhém.
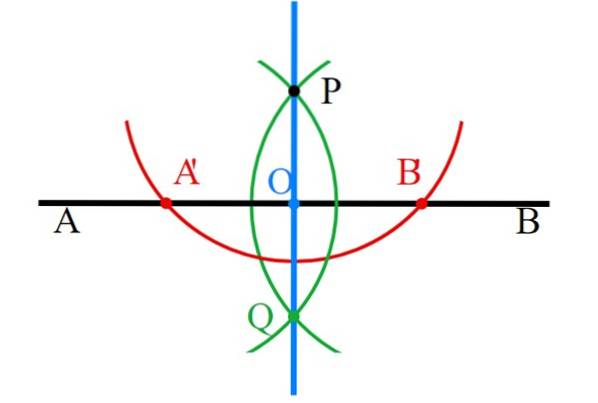
-Body P a Q jsou spojeny s pravítkem a svislá čára (modrá) je připravena.
-Nakonec musí být všechny pomocné konstrukce pečlivě vymazány a ponechány pouze ty kolmé..
- Cvičení 2
Dvě řádky L1 a L.dva jsou kolmé, pokud jejich příslušné svahy m1 a mdva splnit tento vztah:
m1 = -1 / mdva
Vzhledem k přímce y = 5x - 2 najděte přímku kolmou k ní, která prochází bodem (-1, 3).
Řešení
-Nejprve najděte sklon kolmé čáry m⊥, jak je uvedeno v prohlášení. Sklon původní přímky je m = 5, koeficient doprovázející „x“. Pak:
m⊥= -1/5
-Potom se vytvoří rovnice kolmé přímky a⊥, nahrazení dříve nalezené hodnoty:
Y⊥= -1 / 5x + b
-Dále se určí hodnota b pomocí bodu daného výrokem (-1,3), protože jím musí projít kolmá čára:
y = 3
x = -1
Střídání:
3 = -1/5 (-1) + b
Vyřešte hodnotu b:
b = 3- (1/5) = 14/5
-Nakonec je vytvořena definitivní rovnice:
Y⊥= -1 / 5x + 14/5
Reference
- Baldor, A. 2004. Rovina a prostorová geometrie. Kulturní publikace.
- Clemens, S. 2001. Geometrie s aplikacemi a řešením problémů. Addison Wesley.
- Matematika je zábava. Kolmé čáry. Obnoveno z: mathisfun.com.
- Montereyův institut. Kolmé čáry. Obnoveno z: montereyinstitute.org.
- Wikipedia. Kolmé čáry. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře