
Vlastnosti ortogonální matice, důkaz, příklady

Má to ortogonální matice když uvedená matice vynásobená její transpozicí vede k matici identity. Pokud je inverze matice rovna transpozici, pak je původní matice ortogonální.
Ortogonální matice mají charakteristiku, že počet řádků se rovná počtu sloupců. Rovněž řádkové vektory jsou jednotkové ortogonální vektory a transpoziční řádkové vektory také jsou.
Když je ortogonální matice vynásobena vektory vektorového prostoru, produkuje a izometrická transformace, to znamená transformace, která nemění vzdálenosti a zachovává úhly.
Typickým představitelem ortogonálních matic jsou rotační matice. Jsou nazývány transformace ortogonálních matic ve vektorovém prostoru ortogonální transformace.
Geometrické transformace rotace a odrazu bodů představovaných jejich kartézskými vektory se provádějí aplikací ortogonálních matic na původní vektory, aby se získaly souřadnice transformovaných vektorů. Z tohoto důvodu jsou ortogonální matice široce používány při zpracování výpočetní grafiky..
Rejstřík článků
- 1 Vlastnosti
- 2 Demo
- 3 příklady
- 3.1 Příklad 1
- 3.2 Příklad 2
- 3.3 Příklad 3
- 3.4 Příklad 4
- 4 Odkazy
Vlastnosti
Pole M je ortogonální, pokud se vynásobí její transpozicí MT vrátí matici identity Já. Podobně výsledkem produktu transpozice ortogonální matice původní maticí je matice identity:
M MT = M.T M = já
V důsledku předchozího tvrzení máme, že transpozice ortogonální matice se rovná její inverzní matici:
MT = M.-1.
Sada kótovacích ortogonálních matic n x n tvoří skupinu ortogonálních O (n). A podmnožina O (n) ortogonálních matic s determinantem +1 tvoří Skupina unitárních speciálních matic SU (n). Skupinové matice Slunce) jsou matice, které produkují lineární transformace rotace, známé také jako rotační skupina.
Demonstrace
Ukažme si, že matice je ortogonální tehdy a jen tehdy, jsou-li řádkové vektory (nebo sloupcové vektory) vzájemně kolmé a normy 1.
Předpokládejme, že řádky ortogonální matice n x n jsou n orthonormální vektory dimenze n. Pokud je označeno proti1, protidva,…., Vn n vektory jsou splněny:
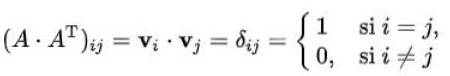
Kde je evidentní, že množina řádkových vektorů je skutečně množina ortogonálních vektorů s normou jedna.
Příklady
Příklad 1
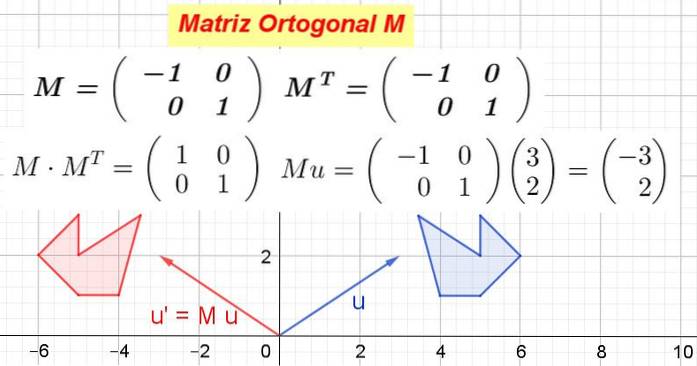
Ukažte, že matice 2 x 2, která má v první řadě vektor v1= (-1 0) a v jeho druhém řádku vektor v2= (0 1) je ortogonální matice.
Řešení: Matice je postavena M a vypočítá se jeho transpozice MT:
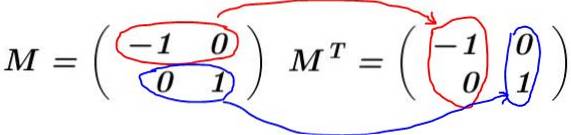
V tomto příkladu pole M je samovolně transponován, to znamená, že matice a její transpozice jsou identické. Znásobuje se M jeho transpozicí MT:
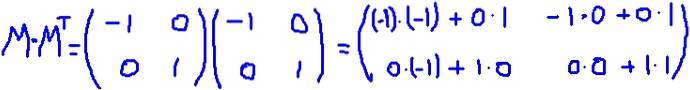
Je ověřeno, že M MT se rovná matici identity:
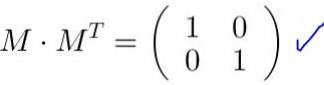
Když matice M se vynásobí souřadnicemi vektoru nebo bodu, získají se nové souřadnice, které odpovídají transformaci, kterou matice provede na vektoru nebo bodu.
Obrázek 1 ukazuje jak M transformovat vektor nebo na nebo' a také jak M přeměňte modrý mnohoúhelník na červený mnohoúhelník. Co M je ortogonální, pak jde o ortogonální transformaci, která zachovává vzdálenosti a úhly.
Příklad 2
Předpokládejme, že máte matici 2 x 2 definovanou v realitách daných následujícím výrazem:
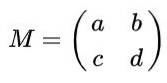
Najděte skutečné hodnoty na, b, C Y d tak, že matice M být ortogonální matice.
Řešení: Podle definice je matice ortogonální, pokud se vynásobí její transpozicí a získá se matice identity. Pamatujeme, že transponovaná matice je získána z originálu, výměnou řádků za sloupce, je získána následující rovnost:
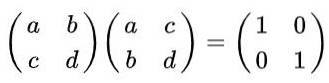
Provádění maticového násobení máme:
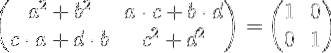
Rovnicí prvků levé matice s prvky matice identity vpravo získáme systém čtyř rovnic se čtyřmi neznámými a, b, c a d.
Navrhujeme následující výrazy pro a, b, c a d, pokud jde o trigonometrické poměry sinus a kosinus:
S tímto návrhem a vzhledem k základní trigonometrické identitě jsou první a třetí rovnice automaticky splněny v rovnosti prvků matice. Třetí a čtvrtá rovnice jsou stejné a v rovnosti matice po nahrazení navrhovaných hodnot to vypadá takto:
což vede k následujícímu řešení:
Nakonec se pro ortogonální matici M získají následující řešení:
Všimněte si, že první z řešení má determinant +1, takže patří do skupiny SU (2), zatímco druhé řešení má determinant -1, a proto do této skupiny nepatří.
Příklad 3
Vzhledem k následující matici najděte hodnoty aab tak, abychom měli ortogonální matici.
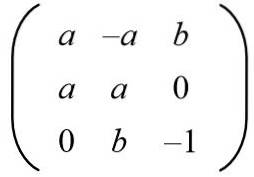
Řešení: Aby byla daná matice ortogonální, musí být produkt s její transpozicí maticí identity. Poté se provede maticový produkt dané matice s transponovanou maticí, čímž se získá následující výsledek:
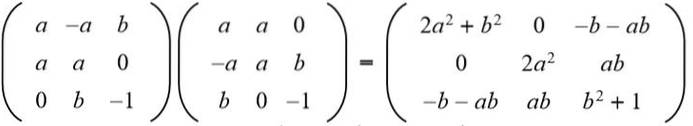
Dále se výsledek rovná matici identity 3 x 3:
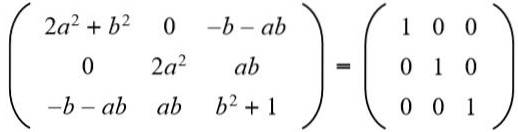
Ve druhém řádku třetím sloupci máme (a b = 0), ale na nemůže to být nula, protože pokud ano, rovnost prvků druhého řádku a druhého sloupce by nebyla splněna. Pak nutně b = 0. Střídání b pro hodnotu 0 máme:
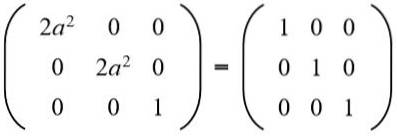
Pak je rovnice vyřešena: 2a ^ 2 = 1, jehož řešení jsou: + ½√2 a -½√2.
Užívání pozitivního řešení pro na získá se následující ortogonální matice:
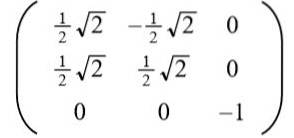
Čtečka může snadno ověřit, že vektory řádků (a také vektory sloupců) jsou ortogonální a jednotné, tj. Ortonormální.
Příklad 4
Dokažte, že matice NA jejichž řádkové vektory jsou v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0 -1) je ortogonální matice. Dále zjistěte, jak jsou transformovány vektory kanonické báze I J K. na vektory u1, u2 Y u3.
Řešení: Mělo by se pamatovat na to, že prvek (i, j) matice vynásobený jeho transpozicí je tečkovým produktem vektoru řádku (i) vektorem sloupce (j) transpozice. Kromě toho se tento produkt rovná Kroneckerově deltě v případě, že je matice ortogonální:
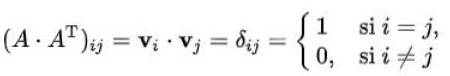
V našem případě to vypadá takto:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
S čím je prokázáno, že se jedná o ortogonální matici.
Co víc u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) a nakonec u3 = A k = (0, 0, -1)
Reference
- Anthony Nicolaides (1994) Determinanty a matice. Předat publikaci.
- Birkhoff a MacLane. (1980). Modern Algebra, ed. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Úvod do lineární algebry. ESIC Editorial.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expansion Theories in Mathematics. Ivy tisk omezen.
- Wikipedia. Ortogonální matice. Obnoveno z: es.wikipedia.com
- Wikipedia. Ortogonální matice. Obnoveno z: en.wikipedia.com


Zatím žádné komentáře