
Charakteristiky točivého momentu a vzorce, cvičení

The točivý moment, točivý moment nebo moment síly je schopnost síly způsobit zatáčku. Etymologicky přijímá název točivého momentu jako odvozeninu od anglického slova točivý moment, z latiny torquere (kroutit).
Točivý moment (vzhledem k danému bodu) je fyzická velikost, která je výsledkem vytvoření vektorového součinu mezi vektory polohy bodu, kde je síla aplikována, a silou vyvíjené síly (v uvedeném pořadí). Tento okamžik závisí na třech hlavních prvcích.
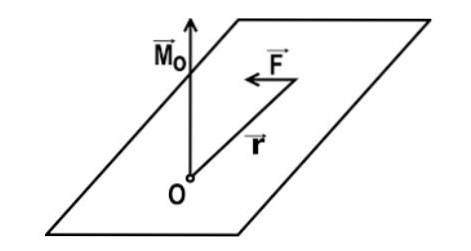
Prvním z těchto prvků je velikost aplikované síly, druhým je vzdálenost mezi bodem, kde je aplikován, a bodem, vůči kterému se tělo otáčí (také nazývané rameno páky), a třetím prvkem je úhel použití uvedené síly.
Čím větší síla, tím větší rotace. Totéž se děje s ramenem páky: čím větší je vzdálenost mezi bodem, kde je síla aplikována, a bodem, vůči kterému vyprodukuje zatáčku, tím větší bude.
Samozřejmě je točivý moment obzvláště zajímavý ve stavebnictví a průmyslu, stejně jako v mnoha domácích aplikacích, například když je matice utažena klíčem..
Rejstřík článků
- 1 vzorce
- 1.1 Jednotky
- 2 Funkce
- 3 Výsledný točivý moment
- 4 Aplikace
- 5 Cvičení vyřešena
- 5.1 Cvičení 1
- 5.2 Cvičení 2
- 6 Reference
Vzorce
Matematické vyjádření točivého momentu síly vzhledem k bodu O je dáno vztahem: M = r x F
V tomto výrazu r je vektor, který spojuje bod O s bodem P aplikace síly, a F je vektor aplikované síly.
Jednotky měření momentu jsou N ∙ m, které, i když jsou rozměrově ekvivalentní Joulovi (J), mají jiný význam a neměly by být zaměňovány.
Proto modul točivého momentu má hodnotu danou následujícím výrazem:
M = r ∙ F ∙ sin α
V tomto výrazu je α úhel mezi vektorem síly a vektorem r nebo ramenem páky. Točivý moment je považován za pozitivní, pokud se tělo otáčí proti směru hodinových ručiček; naopak, je negativní, když se otáčí ve směru hodinových ručiček.
Jednotky
Jak již bylo uvedeno výše, jednotka měření točivého momentu je výsledkem součinu jednotky síly a jednotky vzdálenosti. Konkrétně Mezinárodní systém jednotek používá newtonmetr, jehož symbol je N • m.
Na dimenzionální úrovni se newton metr může zdát ekvivalentní joulu; v žádném případě by se však k vyjádření okamžiků neměl používat červenec. Joule je jednotka pro měření prací nebo energií, které se z koncepčního hlediska velmi liší od torzních momentů.
Stejným způsobem má torzní moment vektorový znak, kterým je jak skalární práce, tak energie.
Vlastnosti
Z toho, co bylo vidět, vyplývá, že točivý moment síly vzhledem k bodu představuje kapacitu síly nebo sady sil k modifikaci rotace uvedeného těla kolem osy, která prochází bodem..
Proto torzní moment generuje úhlové zrychlení na těle a je velikostí vektorového znaku (je tedy definován z modulu, směru a smyslu), který je přítomen v mechanismech, které byly podrobeny kroucení nebo ohybu.
Moment bude nulový, pokud bude mít vektor síly a vektor r stejný směr, protože v takovém případě bude hodnota sin α nulová.
Výsledný točivý moment
Vzhledem k určitému tělesu, na které působí řada sil, působí působící síly ve stejné rovině, točivý moment vyplývající z aplikace všech těchto sil; je součet torzních momentů vyplývajících z každé síly. Proto je pravda, že:
MT = ∑ M = M1 + Mdva + M3 +...
Samozřejmě je nutné vzít v úvahu kritérium znaménka pro torzní momenty, jak je vysvětleno výše.
Aplikace
Točivý moment je přítomen v každodenních aplikacích, jako je utahování matice klíčem nebo otevírání nebo zavírání kohoutku nebo dveří.
Jeho aplikace však jdou mnohem dále; točivý moment se rovněž nachází v osách strojního zařízení nebo v důsledku úsilí, kterému jsou paprsky vystaveny. Proto je jeho použití v průmyslu a mechanice mnoho a rozmanité..

Vyřešená cvičení
Níže uvádíme několik cvičení, která vám usnadní porozumění výše uvedenému.
Cvičení 1
Vzhledem k následujícímu obrázku jsou vzdálenosti mezi bodem O a A a B 10 cm a 20 cm:
a) Vypočítejte hodnotu modulu točivého momentu vzhledem k bodu O, pokud v bodě A působí síla 20 N.
b) Vypočítejte, jaká musí být hodnota síly působící v B, aby se dosáhlo stejného krouticího momentu jako v předchozí části.
Řešení
V první řadě je vhodné přenášet data do jednotek mezinárodního systému.
rNA = 0,1 m
rB = 0,2 m
a) Pro výpočet modulu točivého momentu použijeme následující vzorec:
M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Chcete-li určit požadovanou sílu, postupujte podobným způsobem:
M = r ∙ F ∙ sin α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
Při řešení pro F se získá, že:
F = 10 N.
Cvičení 2
Žena vyvíjí sílu 20 N na konec 30 cm dlouhého klíče. Pokud je úhel síly u rukojeti klíče 30 °, jaký je točivý moment na matici??
Řešení
Použije se následující vzorec a operace se provede:
M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Reference
- Moment síly. (n.d.). Na Wikipedii. Citováno dne 14. května 2018 z es.wikipedia.org.
- Točivý moment (n.d.). Na Wikipedii. Citováno dne 14. května 2018 z en.wikipedia.org.
- Serway, R. A. a Jewett, Jr. J.W. (2003). Fyzika pro vědce a inženýry. 6. vyd. Brooks Cole.
- Marion, Jerry B. (1996). Klasická dynamika částic a systémů. Barcelona: Ed. Reverté.
- Kleppner, Daniel; Kolenkow, Robert (1973). Úvod do mechaniky. McGraw-Hill.



Zatím žádné komentáře