The dvojitý odběr vzorků je technika používaná v inferenční statistice, když chcete vědět více podrobností a jistoty o konkrétní proměnné, která charakterizuje určitou populaci.
Druhý vzorek populace se obvykle provádí po odebrání a analýze prvního vzorku, jehož analýza nepřinesla statisticky významný závěr o žádné ze studovaných proměnných..
Z tohoto důvodu je dvojí vzorkování ve statistice známé také jako dvoustupňový odběr vzorků. Užitečnost druhého vzorku spočívá v tom, že pomáhá s větší přesností určit odhad poměrů a regresí určité pomocné proměnné, který vzniká na základě analýzy prvního vzorku..
Další použití, které se dává dvojímu vzorkování, je shromažďování informací k provádění vzorkování vrstvami..
Níže budou popsány různé situace, kdy je zaručeno dvojí vzorkování..
Metoda dvojitého vzorkování se často používá v průmyslové kontrole kvality a obvykle se provádí ve dvou fázích..
Předpokládejme například průmyslový stroj, který vyrábí určité součásti. Bez ohledu na to, jak je stroj nastaven, žádná část není identická s jinou, protože se mohou vyskytnout malé odchylky v rozměrech a hmotnosti. Jde o určení, zda šarže dílů vyrobených uvedeným strojem splňuje toleranční kritéria, aby mohla být přijata nebo odmítnuta..
Nejprve se odebere náhodný vzorek kusů, pomocí kterého chcete zkontrolovat, zda je jedna z proměnných, například délka kusu, v toleranci.
V případě, že průměrná délka je pod nebo nad úrovní tolerance požadované pro uvedenou proměnnou, v tomto prvním vzorku se odvodí, že šarže je vadná a musí být vyřazena. V tomto případě nejsou vyžadovány žádné nové vzorky.
Naopak, pokud je průměrná hodnota v tolerančním rozmezí, ale směrodatná odchylka vzorku je dostatečně velká, aby sčítání nebo odčítání průměrné hodnoty nespadalo do rozsahu, bude nutné shromáždit druhý větší vzorek..
Tento druhý vzorek musí zahrnovat původní vzorek, aby bylo možné výpočty předělat, a umožnit tak konečné rozhodnutí ohledně vyšetřované proměnné. Tímto způsobem lze zjistit, zda je dávka vadná nebo ne.
Při mnoha příležitostech je obtížné získat informace o jedné z proměnných, které je třeba studovat. Pro sběr dat však může existovat pomocná proměnná snadněji.
V tomto případě jsou odebrány dva vzorky, velký pro pomocnou proměnnou, levnější a menší vzorek, obsažený ve větším vzorku nejdražší proměnné..
Tato metoda je použitelná, kdykoli se zjistí, že existuje korelace mezi oběma proměnnými, což je obecně poměrný vztah..
Příklad této situace se objevuje v lesnických vědách, kde je žádoucí určit procento stromů zasažených parazitickou rostlinou (ringworm).
Jelikož se jedná o velmi rozsáhlé regiony a obtížně přístupné, není studie úplné populace stromů časově a nákladově proveditelná. Následují tyto kroky:
Předběžný odběr vzorků by sestával z použití leteckého snímkování a les je dále rozdělen na části. Odtud je náhodně vybráno několik šarží a pomocí analýzy obrazů vybraných šarží se odhaduje, kolik stromů je ovlivněno kožním červem, protože barva stromů je ovlivněna parazitem..
Fotografická analýza však může být nepřesná, proto je pro práci v terénu vybráno několik dávek prvního vzorku, nejlépe náhodně..
Výsledek pole je poté porovnán s fotografickým pro zachycení dvou sad dávek. Toto srovnání lze provést například vytvořením grafu, ve kterém vodorovná osa je hodnota získaná pro každou dávku fotografií a na svislé ose hodnota získaná pro dávku pomocí terénních prací..
Tato grafická metoda umožňuje vizuálně identifikovat, zda existuje korelace mezi oběma výsledky, a určit pomocí regresní analýzy koeficient proporcionality nebo poměru mezi oběma vzorky..
Po největším vzorku, tj. Po fotografickém vzorku, se vezme průměrná hodnota infikovaných stromů a jejich standardní odchylka. Ale protože byl stanoven koeficient proporcionality a jeho chyba s polními vzorky, je možné opravit výsledek většího vzorku (fotografického).
Tento výsledek lze poté extrapolovat na celou populaci stromu.
V popsaných příkladech je zřejmá výhoda nákladů, protože nahrazení snadno přístupné proměnné jinou obtížně dostupnou proměnnou šetří čas a peníze..
Nevýhodou je, že v případě dvojitého odběru vzorků pro kontrolu kvality existuje riziko procházení dobrými dávkami produktů, které jsou mimo toleranci..
Chceme odhadnout počet nemocných stromů v 162 hektarovém lese. Jelikož je les velmi rozsáhlý, rozděluje se na 100 pozemků stejné oblasti. Náhodně je vybráno 18 pozemků a pomocí fotografické studie se odhaduje, že na těchto 18 pozemcích je 8,5 nemocných stromů se standardní chybou plus nebo minus 4,5 stromu.
Z těchto 18 grafů je náhodně vybráno 8 grafů, ve kterých se provádí terénní studie. U těchto osmi grafů fotografická studie ukazuje 10 nemocných stromů s chybou plus nebo minus 5,3 stromů..
Na druhou stranu u stejných osmi ploch terénní studie ukazuje 12,4 nemocných stromů s chybou plus mínus 6,3 stromů.
Ptá se:
Je vytvořen graf počtu stromů na fotografický počet vs. počet polí pro osm šarží vybraných pro obě studie..
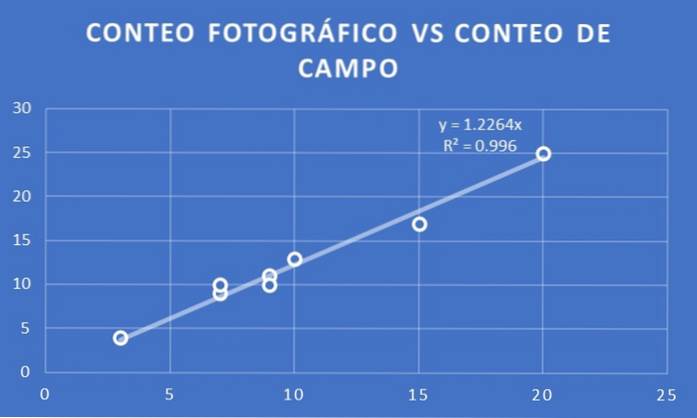
Je uložena trendová čára a je určen její sklon. V tomto případě se získá koeficient proporcionality 1,23. To znamená, že pokud X je počet na počet fotografií, pak se odhaduje, že počet polí bude Y = 1,23 X.
Počet nemocných stromů podle fotografického počtu v 18 vybraných partiích bude:
18 x 8,5 = 153
Ale protože celý les byl rozdělen na 100 pozemků stejné oblasti, počet nemocných stromů odhadovaný fotografickou metodou je: (100/18) x 153 = 850.
Nyní se použije korekční faktor získaný porovnáním mezi polní a fotografickou studií:
Odhadovaný skutečný počet nemocných stromů v lese = 1,23 x 850 = 1046.
Zatím žádné komentáře