
Zvláštní čísla, jak je odlišit, příklady a cvičení
The lichá čísla jsou celá čísla, která nelze dělit číslem 2. To znamená, že s lichým množstvím nemůžete vytvořit skupiny po 2, například pokud má někdo 9 bonbónů, o které se může podělit s přítelem a nechce je dělit, jeden bude mít 4 bonbóny a dalších 5.
Některá lichá čísla jsou následující: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ... V tomto výrazu elipsy označují, že existuje více čísel, nalevo i napravo.

Když se podíváte pozorně, uvidíte, že každé liché číslo lze získat přidáním 2 k předchozímu číslu. Například pokud přidáme 2 až -1, dostaneme 1, pokud uděláme 1 + 2, dostaneme 3 a tak dále.
Rovněž je pozorováno, že pokud jsou páry prokládány, včetně 0, které je považováno za sudé číslo, získá se sada celých čísel Z.
Proto lze jakékoli liché přirozené číslo zapsat ve tvaru 2n + 1, kde n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, kde symbol ± znamená, že n lze brát jako kladné nebo jako negativní.
V případě větších čísel to může být rozpoznáno, když je to liché, protože to vždy končí 1, 3, 5, 7 nebo 9. Například 1571 je liché a stejně tak záporné celé číslo -152,489.
Rejstřík článků
- 1 Zvláštní počet v přírodě a populární kultuře
- 1.1 Prvočísla
- 2 operace lichého čísla
- 2.1 - Součty a produkty
- 2.2 - Pravomoci
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 3.3 - Cvičení 3
- 4 Odkazy
Zvláštní čísla v přírodě a populární kultuře
V přírodě se často vyskytují zvláštní čísla a mezi nimi má číslo 3 zvláštní význam. Podívejme se na několik příkladů:
-Existuje mnoho květin s lichým počtem okvětních lístků.
-Na každé ruce máme 5 prstů.
-Lidé mají 23 párů chromozomů.
-Existují 3 Newtonovy zákony a 3 zákony termodynamiky.
-Jádra atomů, která mají lichý počet protonů a neutronů, jsou méně stabilní než ta, která mají sudý počet.
-Moudří muži jsou 3.
-V příbězích a povídkách se číslo 3 objevuje často, například romány jako Tři mušketýři Alexander Dumas a v lidových povídkách, jako je Tři bratři Y Tři malé prasátka.
-Pro uměleckou kompozici existuje tzv zvláštní pravidlo, což stanoví, že kompozice s lichým počtem prvků je atraktivnější než kompozice se sudým počtem. Liché číslo dodává dynamiku, sudé číslo stabilitu.

-Běžnou strategií, jak zajistit, aby se ceny položek zdály levnější, je jejich konec do 9, řekněme 2,99 $, 39 $ atd..
-Někteří považují číslo 13 za smůlu, zatímco jiní připisují mystické vlastnosti 11, obě lichá čísla..
prvočísla
Prvočísla, ta, která připouštějí pouze sebe a 1 jako dělitele, jsou lichá, s výjimkou 2, což je jediné sudé prvočíslo.
Je možné ukázat, že libovolné číslo lze rozložit jako produkt hlavních faktorů (včetně jejich pravomocí) a že tento způsob vyjádření čísla je jedinečný, s výjimkou pořadí faktorů.
Například číslo 45 lze rozložit na 45 = 33 x 5.
Operace lichého čísla
S lichými čísly se provádějí všechny aritmetické operace a některé mají výrazné charakteristiky.
- Částky a produkty
-Součet dvou lichých čísel má za následek sudé číslo: 3 + 5 = 8; 11 + 15 = 26; (-10) + (+6) = - 4.
-Při přidání lichého čísla k sudému číslu je výsledek lichý: 7 + 2 = 9; 26+ 9 = 35; (-5) + 12 = 7.
-Pokud n výsledkem je první přirozená, lichá a po sobě jdoucí čísla ndva. Podívejme se na to trochu podrobněji:
Pro n = 2: 1 + 3 = 4 = 2dva
Pro n = 3: 1 + 3 + 5 = 9 = 3dva
Pro n = 4: 1 + 3 + 5 + 7 = 16 = 4dva
-Když se lichá hodnota vynásobí sudým, vytvoří se sudé číslo: 7 x 4 = 28; (-3) x 12 = -36.
-Vynásobením dvou lichých čísel získáte také liché: 3 x 5 = 15; (-5) x (+11) = -55.
- Pravomoci
-Když je kladné číslo zvýšeno na lichou mocninu, bude výsledkem kladného čísla, například: 33 = 27.
-Při zvýšení záporného čísla na lichou mocninu je výsledek záporný: (-2)3= (-2) x (-2) x (-2) = -8.
-Liché síly kladných celých čísel lze dosáhnout, pokud jsou lichá čísla uspořádána tak, jak je znázorněno na obrázku, a jsou přidány řádky:
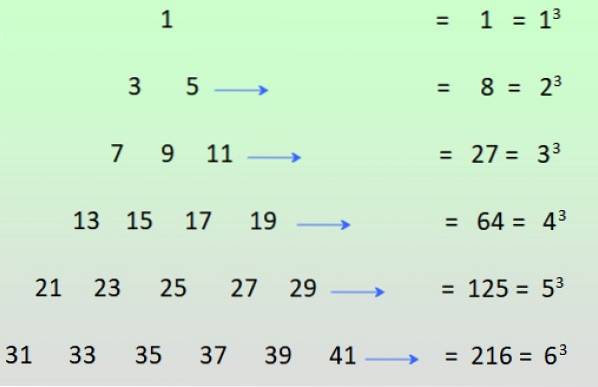
Vyřešená cvičení
- Cvičení 1
Rozhodněte, zda je výsledek následující operace lichý nebo sudý:
(53476890083 + 1987628967) x 13567903
Řešení
Chcete-li získat odpověď, nemusíte běžet hledat kalkulačku, ale spíše použít zobrazené vlastnosti. Podívejme se na poslední číslice sčítání, které jsou 3 a 7:
53476890083 + 1987628967
To znamená, že doplňky jsou liché a my už víme, že součet dvou lichých čísel je sudý.
Proto je číslo, které je výsledkem závorek, sudé a my ho vynásobíme číslem, které končí 3:
13567903
Což znamená, že toto číslo je liché.
Ve vlastnostech popsaných výše bylo zjištěno, že vynásobení sudých x lichých výsledků má sudé číslo. Výsledná operace je proto sudá.
- Cvičení 2
Kolik stojí součet prvních 5 po sobě jdoucích lichých čísel? A co prvních 50?
Řešení
Součet prvních 5 po sobě jdoucích lichých čísel je:
1 + 3 + 5 + 7 + 9 = 25
Ale pokud chceme přidat prvních 50 tímto způsobem, je to těžkopádné, takže přejdeme k vlastnostem. Uvádějí, že součet po sobě jdoucích lichých čísel je ndva. V tomto případě n = 50 a požadovaná částka je:
padesátkadva = 50 x 50 = 2500.
- Cvičení 3
Když přidáte tři po sobě jdoucí lichá čísla, dostanete 237. Jaká jsou čísla?
Řešení
Zavoláme naše první liché číslo x a druhé a z třetí, podle tvrzení platí, že:
x + y + z = 237
V algebraickém jazyce lze libovolné liché číslo napsat ve tvaru 2n +1. Vytvořme naše první liché číslo:
x = 2n +1
Přidejte 2, abychom získali další lichou:
y = x + 2 = (2n + 1) + 2 = 2n + 3
A nakonec se znovu přidá 2, aby se získal třetí lichý:
z = (2n +3) + 2 = 2n + 5
To vše sčítá:
2n + 1 + 2n + 3 + 2n + 5 = 237
6n + 9 = 237
Výsledkem je jednoduchá lineární rovnice, jejíž řešení je:
n = 38
A nyní s hodnotou n = 38 jsou tři požadovaná čísla:
x = (2 × 38) + 1 = 77
Následující jsou tedy po sobě lichá, proto:
y = 79
z = 81
A čtenář může snadno ověřit, že součet všech tří je 237.
Reference
- Baldor, A. 1986. Aritmetika. Vydání a distribuce Codexu.
- Barrios, L. Lichá čísla a mocniny přirozených čísel. Obnoveno z: sinewton.org.
- Brilantní. Sudá a lichá čísla. Obnoveno z: brilliant.org.
- Matematika 18. Operace s lichými čísly. Obnoveno z: matematicas18.com.
- Wikipedia. Sudá a lichá čísla. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře