
Koncept trojrozměrných vln, typy a příklady
Oni jsou trojrozměrné vlny ty, které se šíří ve vesmíru, například zvuková vlna produkovaná reproduktorem. Tato vlna se šíří všemi směry, i když ne se stejnou intenzitou ve všech..
Dojde-li k narušení v bodě v prostoru, šíří se ve třech prostorových směrech, přičemž vlnovými frontami jsou uzavřené povrchy, sférické, eliptické nebo jiného typu..

Na druhou stranu, pokud má místo, odkud vlny pocházejí, tj. Zdroj, plošné rozložení, bude narušení postupovat hlavně ve směru kolmém na uvedenou rovinu a vytvoří čela plochých vln..
Rejstřík článků
- 1 Typy trojrozměrných vln
- 1.1 Rovinné vlny
- 1.2 Válcové vlny
- 1.3 Sférické vlny
- 2 Intenzita a energie sférické vlny
- 3 Příklady trojrozměrných vln
- 3.1 Antény vyzařující elektromagnetické vlny
- 3.2 Seismické vlny
- 3.3 Zvuk
- 4 Odkazy
Typy trojrozměrných vln
V trojrozměrných vlnách jsou čelní strany vln souborem povrchů ponořených do trojrozměrného prostoru.
Nyní je vlnová fronta lokusem bodů v prostoru, které jsou dosaženy počátečním rušením ve stejném okamžiku..
Obvykle se to považuje za tři typy vln, které se pohybují v trojrozměrném prostoru, podle symetrie přední strany vlny: rovinné vlny, válcové vlny a sférické vlny. Skutečné vlny však ne vždy patří k těmto typům, protože nemají tak vysoký stupeň symetrie.
Ploché vlny
Rovinná vlna pohybující se v kladném směru x rychlostí v je funkčně reprezentována jako:
g (x, t) = f (x - v⋅t)
Tato vlna není omezena na osu X, rozšiřuje se také ve směrech Y Y z. Ale funkční forma nám říká, že všechny body, které mají stejnou souřadnici x, bez ohledu na souřadnice (z, y), mají stejnou hodnotu g.
V tomto případě jsou vlnové fronty roviny rovnoběžné s rovinou z-y, které rychle postupují proti, což znamená, že rovinná vlna zabírá celý trojrozměrný prostor.
Výraz představující rovinnou vlnu šířící se jakýmkoli směrem nebo rychle proti, kde nebo představuje jednotkový vektor řídicích kosinů cos (α), cos (β) Y cos (γ), to je:
g = f (û • r - v⋅t) = f (x cos (α) + y cos (β) + z cos (γ) - v⋅t)
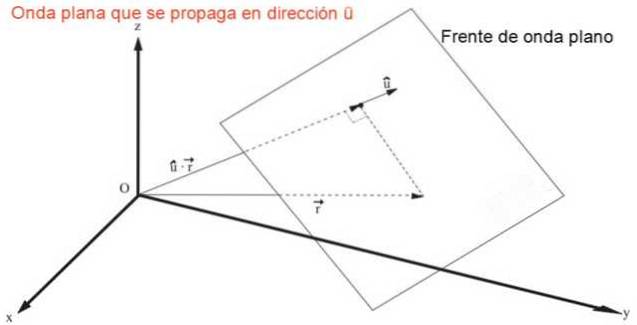
Je snadné ukázat přímou substitucí, že předchozí výraz je řešením trojrozměrné vlnové rovnice, rovnice v parciálních derivacích druhého lineárního řádu:
∂xxg + ∂yyg + ∂zzg = (1 / vdva) ∂ttG
Výše uvedenou rovnici lze psát kompaktněji pomocí laplaciánského operátoru ∇dva:
∇dvag = (1 / vdva) ∂ttG
Válcové vlny
Když je počáteční porucha distribuována po přímce, pak se vlna šíří v radiálním směru kolmém na tuto linii a vyplňuje trojrozměrný prostor, který ji obklopuje, válcovými vlnovými frontami..
Sférické vlny
Když je zdrojem bod a médium, ve kterém se trojrozměrná vlna šíří, je homogenní a izotropní (jeho vlastnosti se nemění podle směru), pak jsou čelní strany vln sférické soustředné k bodu, kde došlo k počátečnímu rušení..
V případě sférické vlny, ve které je intenzita vlny stejná ve všech směrech, závisí funkce popisující poruchu pouze na vzdálenosti r k bodovému zdroji a času t.
V tomto případě máme, že odpovídající Laplacian je:
∇dvag = (1 / rdva) ∂r(rdva ∂rG)
Být vlnovou rovnicí:
∇dvag = (1 / vdva) ∂ttG
Obecným řešením by bylo:
g (r, t) = (1 / r) F (r - v⋅t) + (1 / r) G (r + v⋅t)
V tomto případě se říká, že se jedná o sférická vlna. Ale mohou existovat varianty, jak bude vidět níže
Neizotropní sférické vlny
Může se také stát, že sférická vlna, tj. S vlnovými frontami tvořenými koulemi soustřednými do centrálního bodu, je amplituda nebo intenzita vlny v různých směrech odlišná..
To se stane, když je centrální zdroj vlny účinnější v jednom směru než ostatní..
Například zvuk produkovaný reproduktorem nemá všude stejnou intenzitu, dokonce ani v místech ve stejné vzdálenosti od reproduktoru..
Intenzita není stejná, i když signálu trvá stejný čas, než dosáhne těchto bodů. Je to sférická vlna, která má nesférický směrový vzor.
Máte také sférické vlny v případě elektromagnetických vln vytvářených anténou, ale nemusí být stejně silné ve všech směrech..

Nehomogenní médium
Když je médium nehomogenní, pak se rychlost šíření vlny liší v různých směrech.
Příkladem nehomogenního média je atmosféra, ve které existují tlakové rozdíly s výškou a teplotní gradienty. Dalším příkladem jsou vrstvy zemské kůry, které se liší hustotou a modulem pružnosti..
Nehomogenita vede k tomu, že vlnové fronty pocházející z centrálního bodového zdroje nejsou soustředné sféry, protože vzdálenost uražená vlnou ve stejném časovém období je v každém směru odlišná..
Pak máme trojrozměrnou vlnu, jejíž vlnoplocha není sférická.
Intenzita a energie sférické vlny
Můžeme napsat výraz sférické harmonické vlny takto:
g (r, t) = (gnebo / r) cos (k⋅r - ω⋅t)
Tam, kde se vlnové fronty šíří radiální rychlostí rovnou:
v = ω / k
A jeho amplituda klesá s inverzní vzdáleností r z bodového zdroje sférických vln.
Harmonické vlny mají hustota energie (energie na jednotku objemu) ε dána:
ε = ½ ρ ωdva (Gnebo / r)dva
V této rovnici:
-ρ má jednotky hmotnosti na jednotku objemu a představuje hustotu média, kde se šíří zvuková vlna.
-Gnebo je amplituda posunu prvku média, například kapaliny, v důsledku šířící se vlny.
Je třeba poznamenat, že jelikož se jedná o sférickou vlnu, hustota energie klesá s inverzní funkcí čtverce vzdálenosti.
Intenzita vlny, tj. Energie přenášená za jednotku času, je:
I = v⋅ε
Jako vždy je v praxi nejdůležitější veličinou přenášený výkon na jednotku plochy v radiální vzdálenosti. r:
P = v⋅ε = Inebo / rdva
Bytost Jánebo = ½ ρ v ωdva Gnebodva.
Celková energie přenášená za jednotku času koulí o poloměru r je: P⋅4πrdva= 4π⋅Inebo, a podle očekávání to nezávisí na radiální vzdálenosti.
Příklady trojrozměrných vln
Trojrozměrné vlny jsou velmi časté, takže máme:
Antény vyzařující elektromagnetické vlny

Pokrývají velmi široké spektrum, od rádiových vln mezi stovkami KHz a stovkami MHz, až po vlny vyzařované anténou Wifi řádově v GHz, která již spadá do mikrovlnného rozsahu.
Víme, že mikrovlny, i když nejsou ionizujícím zářením, jsou schopné zvyšovat teplotu těla, protože obsahují hodně vody.
Proto se nedoporučuje mít wi-fi anténu blízko hlavy nebo těla. Stačí se trochu vzdálit, protože při dvojnásobné vzdálenosti je intenzita čtvrtou částí.
Seismické vlny
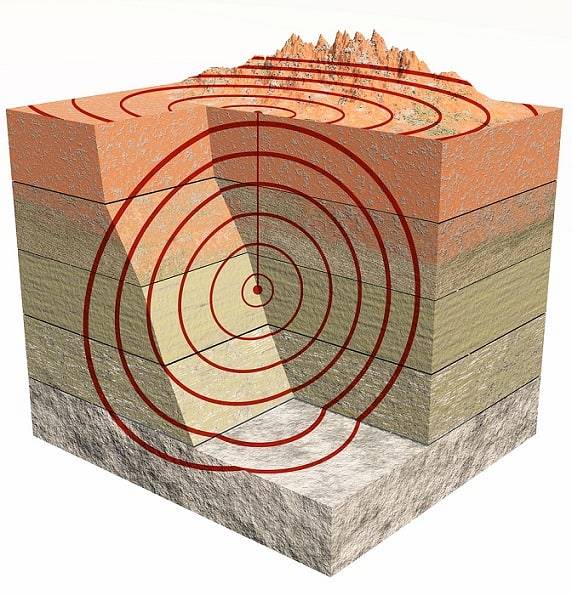
Jsou to také trojrozměrné vlny. Hlavně existují typy P co jsou kompresní vlny a ty typu S které jsou řezání nebo stříhání (sslyšet v angličtině).
Vlny P nebo primárky dorazí jako první, protože se šíří rychleji než vlny S nebo sekundární.
Zvuk

Zvuk je typ trojrozměrné vlny. Tyto vlny se šíří všemi směry, i když, jak jsme již řekli, ne se stejnou intenzitou ve všech směrech..
Důvodem je, že zdroj zvuku ne vždy vyzařuje dokonale sférickou symetrii.
Reference
- Baranek, L. 1969. Akustika. 2. místo Edice. Mcgraw kopec.
- Griffiths G. Lineární a nelineární vlny. Obnoveno z: scholarpedia.org.
- Nottoli, H. 2004. Fyzika aplikovaná na architekturu. Nobuko.
- Whitham G.B. 1999. Lineární a nelineární vlny. Wiley.
- Wikiwaves. Nelineární vlny. Obnoveno z: wikiwaves.org



Zatím žádné komentáře