
Definice, vlastnosti a příklady hyperbolických paraboloidů

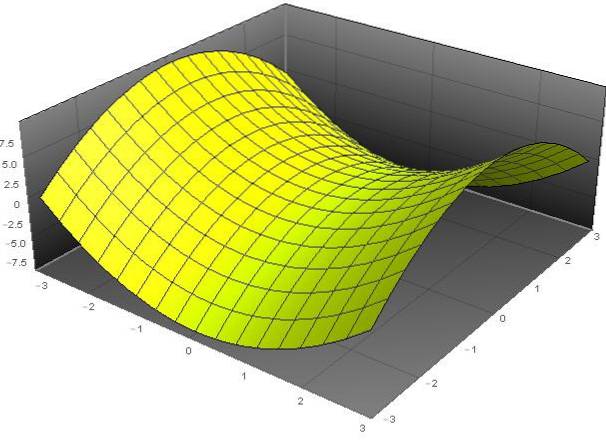
A hyperbolický paraboloid je povrch, jehož obecná rovnice v kartézských souřadnicích (x, y, z) splňuje následující rovnici:
(pro)dva - (a / b)dva - z = 0.
Název „paraboloid“ vychází ze skutečnosti, že proměnná z závisí na čtvercích proměnných xay. Zatímco přídavné jméno „hyperbolický“ je způsobeno skutečností, že při pevných hodnotách z máme rovnici hyperboly. Tvar tohoto povrchu je podobný jako u koňského sedla.
Rejstřík článků
- 1 Popis hyperbolického paraboloidu
- 2 Vlastnosti hyperbolického paraboloidu
- 3 Pracované příklady
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 3.3 - Příklad 3
- 4 Hyperbolický paraboloid v architektuře
- 5 Reference
Popis hyperbolického paraboloidu
Abychom pochopili podstatu hyperbolického paraboloidu, bude provedena následující analýza:
1. - Vezmeme konkrétní případ a = 1, b = 1, to znamená, že kartézská rovnice paraboloidu zůstane jako z = xdva - Ydva.
2. - Roviny rovnoběžné s rovinou ZX jsou považovány, tj. Y = ctte.
3. - U y = ctte zůstává z = xdva - C, které představují paraboly s větvením nahoru a vrcholem pod rovinou XY.
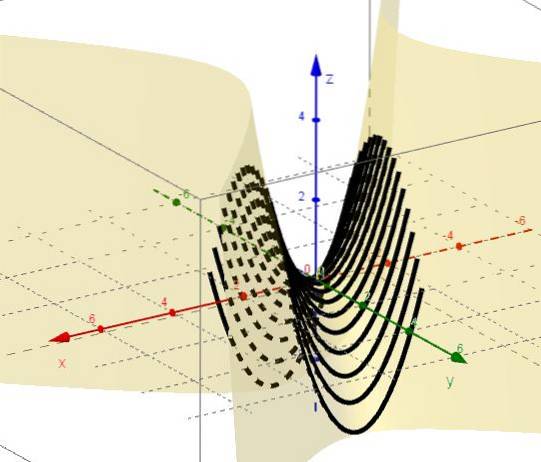
4. - S x = ctte zůstává z = C - ydva, které představují paraboly s větvemi dolů a vrcholem nad rovinou XY.
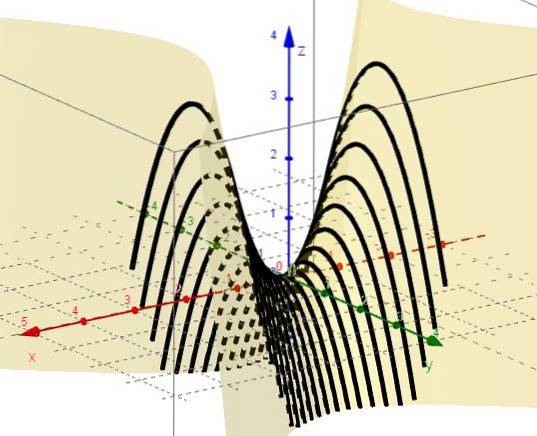
5. - Se z = ctte zůstane C = xdva - Ydva, které představují hyperboly v rovinách rovnoběžných s rovinou XY. Když C = 0, existují dvě čáry (na + 45 ° a -45 ° vzhledem k ose X), které se protínají v počátku v rovině XY.
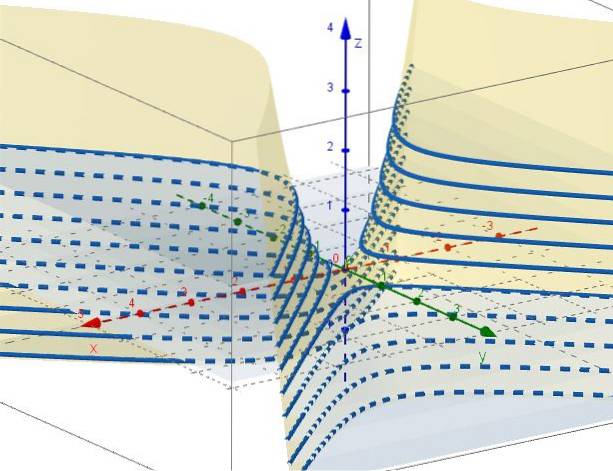
Vlastnosti hyperbolického paraboloidu
1.- Čtyři různé body v trojrozměrném prostoru definují jeden a jediný hyperbolický paraboloid.
2. - Hyperbolický paraboloid je a dvojnásobně ovládaný povrch. To znamená, že navzdory tomu, že jde o zakřivený povrch, procházejí každým bodem hyperbolického paraboloidu dvě různé čáry, které zcela patří hyperbolickému paraboloidu. Druhý povrch, který není rovinou a je dvojnásobně ovládán, je hyperboloid revoluce.
Je to právě druhá vlastnost hyperbolického paraboloidu, která umožnila jeho široké použití v architektuře, protože povrch může být generován z paprsků nebo přímých lan..
Druhá vlastnost hyperbolického paraboloidu umožňuje jeho alternativní definici: je povrch, který lze generovat pohybující se přímkou rovnoběžnou s pevnou rovinou a řeže dvě pevné čáry, které slouží jako vodítko. Následující obrázek objasňuje tuto alternativní definici hyperbolického paraboloidu:
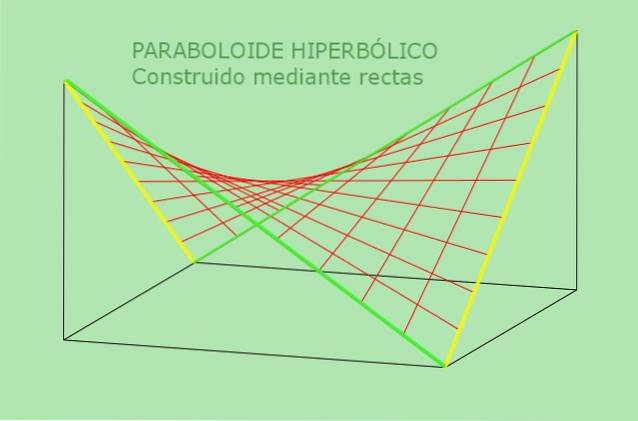
Pracoval příklady
- Příklad 1
Ukažte, že rovnice: z = xy, odpovídá hyperbolickému paraboloidu.
Řešení
Transformace bude použita na proměnné x a y odpovídající rotaci kartézských os vzhledem k ose Z + 45 °. Staré souřadnice xay jsou transformovány na nové x 'a y' podle následujících vztahů:
x = x '- y'
y = x '+ y'
zatímco souřadnice z zůstává stejná, tj. z = z '.
Dosazením do rovnice z = x máme:
z '= (x' - y ') (x' + y ')
Použitím pozoruhodného součinu rozdílu o součet rovný rozdílu čtverců máme:
z '= x'dva - Y 'dva
což jasně odpovídá původně dané definici hyperbolického paraboloidu.
Zachycení rovin rovnoběžných s osou XY hyperbolickým paraboloidem z = x a určení rovnostranných hyperbolas, které mají asymptoty rovin x = 0 a y = 0.
- Příklad 2
Určete parametry na Y b hyperbolického paraboloidu, který prochází body A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) a D (2, -1, 32/9).
Řešení
Podle jeho vlastností určují čtyři body v trojrozměrném prostoru jeden hyperbolický paraboloid. Obecná rovnice je:
z = (x / a)dva - (a / b)dva
Dosazujeme dané hodnoty:
Pro bod A máme 0 = (0 / a)dva - (0 / b)dva, rovnice, která je splněna bez ohledu na hodnoty parametrů a a b.
Dosazením bodu B získáme:
5/9 = 1 / adva - 1 Bdva
Zatímco pro bod C zůstává:
32/9 = 4 / adva - 1 Bdva
Nakonec pro bod D získáme:
32/9 = 4 / adva - 1 Bdva
Což je totožné s předchozí rovnicí. Nakonec musí být vyřešen systém rovnic:
5/9 = 1 / adva - 1 Bdva
32/9 = 4 / adva - 1 Bdva
Odečtením druhé rovnice od první získáme:
27/9 = 3 / adva z čehož vyplývá, že adva = 1.
Podobně se druhá rovnice odečte od čtyřnásobku první a získá se:
(32-20) / 9 = 4 / adva - 4 / adva -1 Bdva + 4 / bdva
Což je zjednodušeno jako:
12/9 = 3 / bdva ⇒ bdva = 9/4.
Stručně řečeno, hyperbolický paraboloid, který prochází danými body A, B, C a D, má kartézskou rovnici danou:
z = xdva - (4/9) adva
- Příklad 3
Podle vlastností hyperbolického paraboloidu procházejí každým bodem dvě linie, které jsou v něm zcela obsaženy. Pro případ z = x ^ 2 - y ^ 2 najděte rovnici dvou linií, které procházejí bodem P (0, 1, -1), jasně patřícímu hyperbolickému paraboloidu, takže všechny body těchto linek také patří na stejné.
Řešení
Pomocí pozoruhodného součinu rozdílu čtverců lze rovnici pro hyperbolický paraboloid napsat takto:
(x + y) (x - y) = c z (1 / c)
Kde c je nenulová konstanta.
Rovnice x + y = c z a rovnice x - y = 1 / c odpovídají dvěma rovinám s normálními vektory n=<1,1,-c> Y m=<1,-1,0>. Vektorový produkt m x n =<-c, -c, -2> udává směr průsečíku obou rovin. Pak jedna z přímek, která prochází bodem P a patří k hyperbolickému paraboloidu, má parametrickou rovnici:
Pro určení c dosadíme bod P v rovnici x + y = c z, získáme:
c = -1
Podobným způsobem, ale vzhledem k rovnicím (x - y = k z) a (x + y = 1 / k) máme parametrickou rovnici přímky:
Stručně řečeno, dva řádky:
Jsou zcela obsaženy v hyperbolickém paraboloidu z = xdva - Ydva procházející bodem (0, 1, -1).
Pro kontrolu předpokládejme, že t = 1, které nám dává bod (1,2, -3) na prvním řádku. Musíte zkontrolovat, zda je také na paraboloidu z = xdva - Ydva:
-3 = 1dva - dvadva = 1 - 4 = -3
Což potvrzuje, že skutečně patří k povrchu hyperbolického paraboloidu.
Hyperbolický paraboloid v architektuře

Hyperbolický paraboloid využívají v architektuře velcí avantgardní architekti, mezi nimiž vynikají jména španělského architekta Antoniho Gaudího (1852-1926) a zvláště také španělského Félixe Candely (1910-1997)..
Níže jsou uvedena některá díla založená na hyperbolickém paraboloidu:
-Kaple města Cuernavaca (Mexiko) dílo architekta Félixe Candely.
-Oceánografie ve Valencii (Španělsko), také Félix Candela.
Reference
- Encyklopedie matematiky. Vládl povrch. Obnoveno z: encyclopediaofmath.org
- Llera Rubén. Hyperbolický paraboloid. Obnoveno z: rubenllera.wordpress.com
- Weisstein, Eric W. „Hyperbolický paraboloid.“ Z webového zdroje MathWorld-A Wolfram. Obnoveno z: mathworld.wolfram.com
- Wikipedia. Paraboloid. Obnoveno z: en.wikipedia.com
- Wikipedia. Paraboloid. Obnoveno z: es.wikipedia.com
- Wikipedia. Vládl povrch. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře