Sklon přímkového vzorce a rovnic, reprezentace, příklady

The sklon přímky je tečna úhlu θ, kterou uvedená čára tvoří s vodorovnou osou, která se podle konvence měří proti směru hodinových ručiček. Sklon jakékoli přímky je vždy konstantní, a proto je jednou z jejích nejdůležitějších charakteristik..

Chcete-li to vypočítat, potřebujete znát dva body na přímce, jejichž souřadnice jsou (x₁,Y₁) a (x_dva,Y_dva). Mezi oběma body je nakreslen segment, který patří k přímce, a potom jsou nakresleny segmenty, které představují vzdálenost mezi x.₁ a x_dva, a mezi a₁ a a_dva, jako na obrázku níže.

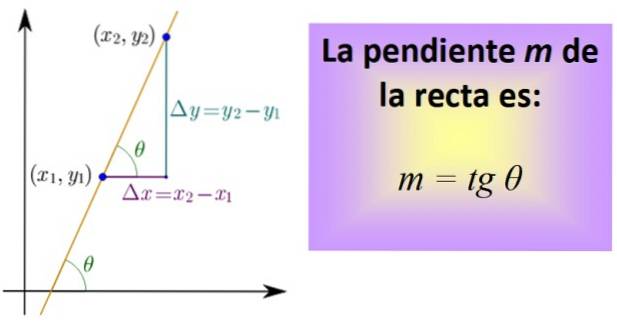
Tyto tři segmenty tvoří pravý trojúhelník, jehož nohy jsou: Δx = x_dva - X₁  y Δy = y_dva - Y₁. Odpovídají vodorovnému a svislému posunutí..

Nyní definujeme kvocient, který se nazývá tečna úhlu θ a zkráceně tg θ, což je přesně sklon m přímky:

m = tg θ = Δy / Δx

U čáry zůstává tento úhel konstantní bez ohledu na body, které byly použity k výpočtu její tečny. V každém případě nám tato hodnota udává míru strmosti čáry.

Prostřednictvím souřadnic vybraných bodů je vzorec pro sklon:

m = (y - y₁ ) / (X_dva - X₁)

Rejstřík článků

• 1 Grafické znázornění
• 2 Druhy svahu
• 3 Jak vypočítáte sklon přímky?
• 4 Vyřešená cvičení
  • 4.1 - Cvičení 1
  • 4.2 - Cvičení 2
• 5 příkladů
  • 5.1 Příklad 1
  • 5.2 Příklad 2
• 6 Reference

Grafické znázornění

Níže máme několik situací, ve kterých je koncept sklonu relevantní. Jeho hodnotu lze snadno vypočítat změřením příslušného svislého a vodorovného posunutí a následným vytvořením kvocientu uvedeného na začátku.

To nám dává představu o nerovnostech nebo úpadku nějaké struktury, jako je rampa, střecha nebo silnice:

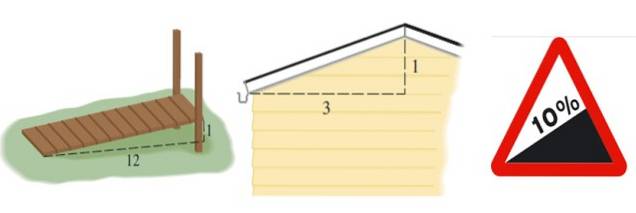
Sklon rampy zobrazené na obrázku 2 vlevo je m = 1/12, sklon střechy je m = 1/3 a sklon silnice je vyjádřen v procentech. Procento 10% znamená, že na každých 100 metrů, které postupují vodorovně, se získá 10 metrů na výšku:

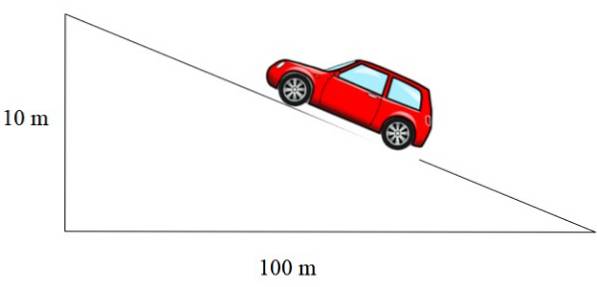
V tomto případě je sklon 10/100 = 0,1, což, vyjádřeno v procentech, se rovná 10%..

Typy svahů

Sklon přímky může být kladný, záporný nebo nulový. Například čára znázorněná na obrázku 1 má kladný sklon. Oceňujeme to okamžitě, protože vidíme, že čára „stoupá“, pokud ji vidíme zleva doprava.

Pokud čára sestupuje zleva doprava, její sklon je záporný. A když je čára vodorovná, její sklon je nulový.

Nakonec u svislých čar není sklon definován.

Grafické znázornění každého typu je níže:

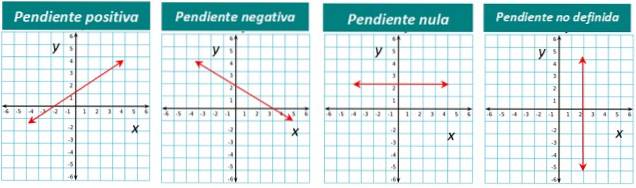
Jak vypočítáte sklon čáry?

Výpočet sklonu je velmi jednoduchý, stačí najít svislé posunutí a vodorovné posunutí a poté vytvořit kvocient mezi oběma.

Když máme kresbu čáry v kartézské rovině, jsou tato posunutí nalezena výběrem libovolných dvou bodů na přímce P₁ A str_dva, určení jeho souřadnic a použití definice uvedené na začátku:

m = (y - y₁ ) / (X_dva - X₁ )

Protože hodnota sklonu je nezávislá na volbě P₁ A str_dva , vybereme bod P libovolnou ze souřadnic (x, y), která patří k přímce, jejíž souřadnice nejsou známy, a další bod P₁ jehož souřadnice jsou: (x₁,Y₁).

Sklon je:

m = (y - y₁) / (x - x₁)

Můžeme vyčistit Y:

a - a₁ = m (x - x₁)

Nyní předpokládejme, že bod P₁ je průsečík přímky se svislou osou souřadnic (0, b). Dosazením do výše uvedené rovnice:

y - b = m (x - 0) → y = mx + b

Tento výraz je znám jako rovnice přímky ve tvaru sklon - průsečík, protože přímka je jednoznačně určena, jsou-li známy její sklon a její průsečík se svislou osou.

Znát pouze sklon nestačí k charakterizaci přímky v rovině, protože nekonečné čáry mohou mít stejný sklon, což znamená, že jsou rovnoběžné, ale procházejí jinými body.

Vyřešená cvičení

- Cvičení 1

Najděte sklon přímky zobrazené na následujícím obrázku:

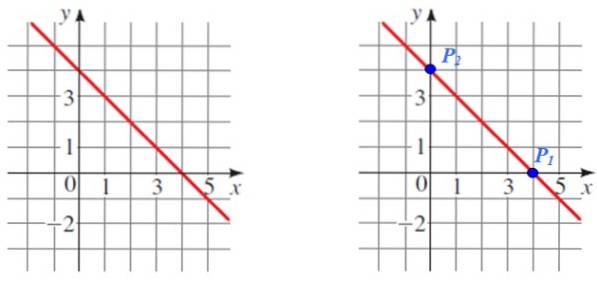
Řešení

P₁ A str_dva jsou dva snadno čitelné body, které budou použity pro výpočet, nezapomeňte také, že se jedná o příslušné průsečíky s osami souřadnic.

Souřadnice každého bodu jsou:

P₁ (4.0) a P_dva (0,4)

Dosazením do rovnice pro sklon:

m = (4 - 0) / (0-4) = 4 / (- 4) = -1

Sklon je záporný, což se dalo očekávat po pohledu na graf.

- Cvičení 2

Najděte rovnici přímky, která prochází bodem (1, -6) a je rovnoběžná s přímkou ​​y = 2x - 3.

Řešení

Sklon hledané přímky musí být stejný jako sklon y = 2x - 3, protože jsou rovnoběžné. Pro tuto přímku je sklon m = 2, proto hledaná má tvar:

a - a₁ = 2 (x - x₁)

Nyní dosadíme bod, kterým prochází naše přímka: x₁ = 1 a y₁ = -6.

y - (-6) = 2 (x - 1)

Proto y = 2x - 2 - 6 → y = 2x - 8

Příklady

Dvě veličiny lze spojit tak, že jejich graf je přímka. V takovém případě se říká, že veličiny mají lineární závislost a sklon přímky lze interpretovat jako rychlost změny z jedné proměnné na druhou.

Příklad 1

Předpokládejme, že bazén je naplněn vodou v a hodnotit konstantní v čase. Přirozeně, čím více času uplyne, tím více vody se uskladní. Rychlost plnění bazénu je přesně sklon čáry, která spojuje objem s časem:

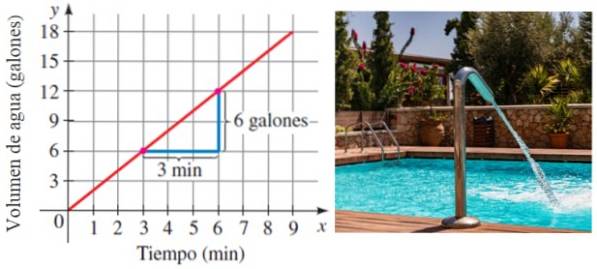
V tomto příkladu se bazén plní rychlostí 6/3 galonů za minutu nebo 2 galony za minutu.

Příklad 2

Když se mobil pohybuje v přímce konstantní rychlostí, sklon pozičního grafu jako funkce času není nic jiného než uvedená rychlost. Graf ukazuje mobil s pozitivní rychlostí, což znamená, že se pohybuje od počátku.

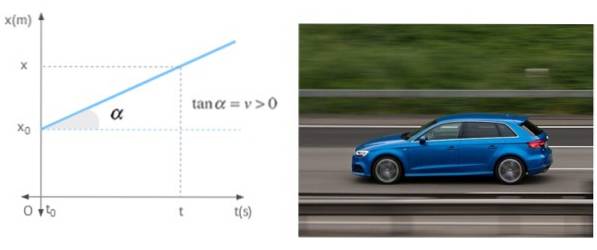
Reference

1. Alvarez, J. Svah dálnice. Obnoveno z: geogebra.es.
2. Carena, M. 2019. Pre-University Matematická příručka. Národní univerzita v Litoralu.
3. Hoffman, J. Výběr témat matematiky. Svazek 4.
4. Jiménez, R. 2008. Algebra. Hala Prentice.
5. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Edice. Cengage Learning.
6. Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.