V izobarický proces, tlak P systému zůstává konstantní. Předpona „iso“ pochází z řečtiny a používá se k označení, že něco zůstává konstantní, zatímco „baros“, také z řečtiny, znamená váhu.
Izobarické procesy jsou velmi typické jak v uzavřených nádobách, tak v otevřených prostorech, protože je lze snadno lokalizovat v přírodě. Tím myslíme, že jsou možné fyzikální a chemické změny na zemském povrchu nebo chemické reakce v nádobách otevřených do atmosféry..
Některé příklady lze získat zahřátím balónku naplněného vzduchem na slunci, vařením, vařením nebo zamrzáním vody, párou vytvářenou v kotlích nebo postupem zvedání horkovzdušného balónu. Později vysvětlíme tyto případy.
Rejstřík článků
Odvozme rovnici pro izobarický proces za předpokladu, že studovaný systém je ideální plyn, model docela vhodný pro téměř jakýkoli plyn při tlaku nižším než 3 atmosféry. Částice ideálního plynu se pohybují náhodně a zabírají celý objem prostoru, který je obsahuje, aniž by na sebe vzájemně působily..
Pokud se nechá ideální plyn uzavřený ve válci opatřeném pohyblivým pístem pomalu expandovat, lze předpokládat, že jeho částice jsou po celou dobu v rovnováze. Poté plyn působí na píst oblasti NA síla F o velikosti:
F = p.A
Kde p je tlak plynu. Tato síla vyvíjí práci a vytváří nekonečně malý posun dx na pístu dané:
dW = Fdx = pA.dx
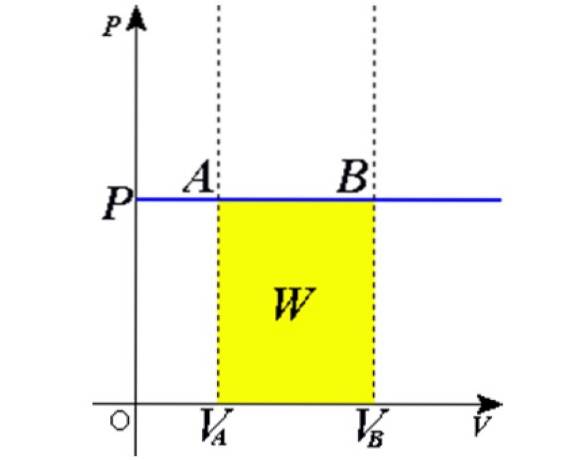
Jako produkt Adx je objemový rozdíl dV, pak dW = pdV. Zbývá integrovat obě strany od počátečního objemu PROTINA do konečného objemu PROTIB získat celkovou práci provedenou plynem:
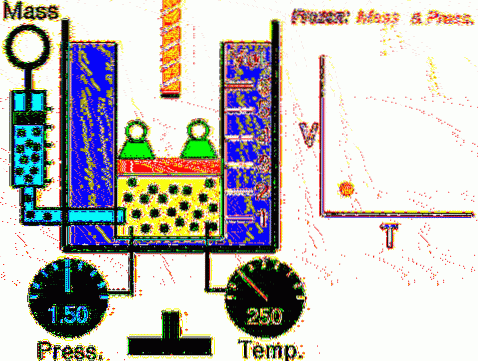
Popsaná situace se experimentálně ověřuje omezením plynu uvnitř válce opatřeného pohyblivým pístem, jak je znázorněno na obrázcích 2 a 3. Na píst je umístěna hmotnost o hmotnosti M, jejíž hmotnost směřuje dolů, zatímco plyn působí síla vzhůru díky tlaku P vyvíjenému na píst.
Jelikož se píst může volně pohybovat, objem, který plyn zaujímá, se může bez problémů změnit, ale tlak zůstává konstantní. Sčítání atmosférického tlaku Pbankomat, který také vyvíjí sílu dolů, máme:
Mg - P.A + Pbankomat . A = konstantní
Proto: P = (Mg / A) + Pbankomat nemění se, pokud nedojde ke změně M a tím i hmotnosti. Přidáním tepla do válce bude plyn expandovat zvětšením svého objemu nebo se bude stahovat při získávání tepla..
Stavová rovnice ideálního plynu souvisí s důležitými proměnnými: tlak P, objem V a teplota T:
P.V = n .R.T.
Zde n představuje počet molů a R je konstanta ideálního plynu (platí pro všechny plyny), která se vypočítá vynásobením Boltzmannovy konstanty číslem Avogadra, což má za následek:
R = 8,31 J / mol K.
Když je tlak konstantní, lze stavovou rovnici zapsat jako:
V / T = nR / P
Ale nR / P je konstantní, protože n, R a P jsou. Když tedy systém přejde ze stavu 1 do stavu 2, nastane následující poměr, známý také jako Charlesův zákon:
PROTI1/ T1 = Vdva/ Tdva
Nahrazení v W = PΔV, získá se práce pro přechod ze stavu 1 do stavu 2, pokud jde o konstanty a kolísání teploty, snadno měřitelné pomocí teploměru:
Ž1 → 2 = nR (T.dva - T1) = nR.ΔT
Na druhé straně první zákon termodynamiky uvádí, že:
∆U = Q - W
To znamená, že přidání určitého množství tepla Q k plynu zvyšuje vnitřní energii ∆U a zvyšuje vibrace jeho molekul. Tímto způsobem se plyn rozpíná a pracuje pohybem pístu, jak jsme již řekli dříve..
V monatomickém ideálním plynu a variaci vnitřní energie ∆U, která zahrnuje jak kinetickou energii, tak potenciální energii jeho molekul, je:
∆U = (3/2)nR ΔT
Nakonec spojíme výrazy, které jsme získali, do jednoho:
Q = ∆U + W = (3/2)nR ΔT + nR=T = (5/2) nR ΔT
Alternativně lze Q přepsat z hlediska hmotnosti m, teplotního rozdílu a nové konstanty měrné teplo plynu při stálém tlaku, zkráceně cp, jehož jednotky jsou J / mol K:
Q = m cp .T
Ne všechny izobarické procesy se provádějí v uzavřených nádobách. Ve skutečnosti dochází při atmosférickém tlaku k nesčetným termodynamickým procesům všeho druhu, takže izobarické procesy jsou v přírodě velmi časté. To zahrnuje fyzikální a chemické změny na zemském povrchu, chemické reakce v nádobách otevřených do atmosféry a mnoho dalšího..
Aby se v uzavřených systémech mohly vyskytnout izobarické procesy, musí být jejich hranice dostatečně flexibilní, aby umožňovaly změny objemu bez změny tlaku.
To se stalo při experimentu s pístem, který se snadno pohyboval, jak se plyn rozpínal. Totéž se děje s uzavřením plynu ve večírku nebo horkovzdušném balónu.
Zde máme několik příkladů izobarických procesů:
Vařící voda na čaj nebo omáčky na vaření v otevřených nádobách jsou dobrým příkladem izobarických procesů, protože všechny probíhají za atmosférického tlaku..
Jak se voda ohřívá, zvyšuje se teplota a objem a pokud se teplo stále přidává, konečně se dosáhne bodu varu, ve kterém dochází k fázové změně vody z kapaliny na vodní páru. I když k tomu dojde, teplota také zůstane konstantní na 100 ° C..
Na druhou stranu je mrznoucí voda také isobarický proces, ať už probíhá v jezeře v zimě nebo v domácí lednici..
Dalším příkladem izobarického procesu je změna objemu balónu nafouknutého vzduchem, když je vystaven slunci. První věc ráno, když ještě není příliš horko, má balón určitý objem..
Jak čas plyne a teplota se zvyšuje, balón se také zahřívá, zvětšuje svůj objem a k tomu všemu dochází při stálém tlaku. Materiál balónku je dobrým příkladem okraje, který je dostatečně pružný, takže vzduch uvnitř se při zahřátí rozpíná bez úpravy tlaku.
Zážitek lze provést také nastavením nenaplněného balónku ve výtoku skleněné láhve naplněné třetinou vody, která se ohřívá v zátoce. Jakmile se voda ohřeje, balón se okamžitě nafoukne, ale je třeba dbát na to, aby se příliš nezahřívalo, aby nevybuchl..
Jedná se o plovoucí loď bez pohonu, která využívá vzdušné proudy k přepravě osob a předmětů. Balón je obvykle naplněn horkým vzduchem, který je chladnější než okolní vzduch a stoupá a rozpíná se, což způsobí, že balón stoupá..
Ačkoli proudy vzduchu směrují balón, má hořáky, které jsou aktivovány k ohřevu plynu, když je požadováno stoupání nebo udržování výšky, a deaktivují se při sestupu nebo přistání. To vše se děje za atmosférického tlaku, předpokládaného konstantní v určité výšce nedaleko od povrchu..
Pára se v kotlích vytváří ohřevem vody a udržováním konstantního tlaku. Poté tato pára provádí použitelnou práci, například vyrábí elektřinu v termoelektrických zařízeních nebo aktivuje další mechanismy, jako jsou lokomotivy a vodní čerpadla..
K dispozici je 40 litrů plynu o teplotě 27 ° C. Zjistěte nárůst objemu, když se izobaricky přidává teplo, dokud nedosáhnete 100 ° C.
Charlesův zákon se používá k určení konečného objemu, ale Pozornost: teploty musí být vyjádřeny v kelvinech, ke každému přidáme pouze 273 K.
27 ° C = 27 + 273 K = 300 K.
100 ° C = 100 + 273 K = 373 K.
Z:
PROTI1/ T1 = Vdva/ Tdva ⇒ Vdva = Tdva(PROTI1/ T1) = 373 ° C (40 l / 300 K) = 49,7 l
Nakonec je nárůst objemu Vdva - PROTI1 = 49,7 l - 40 l = 9,7 l.
Dodáváno 5,00 x 103 J energie na ideální plyn k výkonu 2,00 x 103 J pracuje na svém prostředí v izobarickém procesu. Je žádáno, aby našel:
a) Změna vnitřní energie plynu.
b) Změna objemu, pokud nyní vnitřní energie poklesne o 4,50 x 103 J a 7,50 x 10 jsou vysunuty3 J systému, s ohledem na konstantní tlak 1,01 x 105 Pa.
Použitý ∆U = Q - W a hodnoty uvedené v prohlášení jsou nahrazeny: Q = 5,00 x 103 J a W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Proto se vnitřní energie plynu zvyšuje o 3,00 x 103 J.
Změna hlasitosti se nachází v provedené práci: W = P∆V:
∆U = Q - W = Q - P∆V
Prohlášení uvádí, že vnitřní energie klesá, proto: ∆U= -4,50 x 103 J. Také nám říká, že je vyloučeno určité množství tepla: Q = -7,50 x 103 J. V obou případech negativní znaménko představuje pokles a ztrátu, takže:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Kde P = 1,01 x 105 Pa. Protože jsou všechny jednotky v mezinárodním systému, pokračujeme v řešení změny objemu:
=V = (-4,50 x 103 J +7,50 x 103 J) / (- 1,01 x 105 Pa) = -2,97 x 10-dva m3
Jelikož je změna objemu záporná, znamená to, že se objem snížil, to znamená, že se systém smrštil.
Zatím žádné komentáře