
Vlastnosti, aplikace a cvičení napříč produkty
The křížový produkt nebo vektorový produkt je to způsob násobení dvou nebo více vektorů. Existují tři způsoby, jak násobit vektory, ale žádný z nich není násobení v obvyklém smyslu slova. Jedna z těchto forem je známá jako vektorový produkt, který nám jako výsledek dává třetí vektor.
Křížový produkt, který se také nazývá křížový produkt nebo vnější produkt, má různé algebraické a geometrické vlastnosti. Tyto vlastnosti jsou velmi užitečné, zejména při studiu fyziky..

Rejstřík článků
- 1 Definice
- 2 Vlastnosti
- 2.1 Majetek 1
- 2.2 Majetek 2
- 2.3 Majetek 3
- 2.4 Vlastnost 4 (produkt se třemi tečkami)
- 2.5 Vlastnost 5 (trojitý vektorový produkt)
- 2.6 Majetek 6
- 2.7 Majetek 7
- 2.8 Majetek 8
- 3 Aplikace
- 3.1 Výpočet objemu rovnoběžnostěnu
- 4 Vyřešená cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Definice
Formální definice vektorového produktu je následující: pokud A = (a1, a2, a3) a B = (b1, b2, b3) jsou vektory, pak vektorový produkt A a B, který označíme jako AxB, je:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
Kvůli zápisu AxB se čte jako „kříž B“.
Příkladem použití vnějšího produktu je, že pokud A = (1, 2, 3) a B = (3, -2, 4) jsou vektory, pak pomocí definice vektorového produktu máme:
AxB = (1, 2, 3) x (3, -2, 4) = (2 * 4 - 3 * (- 2), 3 * 3 - 1 * 4, 1 * (- 2) - 2 * 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
Další způsob vyjádření vektorového produktu je dán zápisem determinantů.
Výpočet determinantu druhého řádu je dán vztahem:
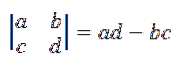
Vzorec pro křížový produkt uvedený v definici lze proto přepsat takto:
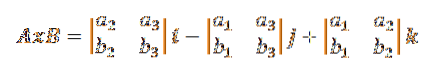
Toto je obvykle zjednodušeno na determinant třetího řádu takto:
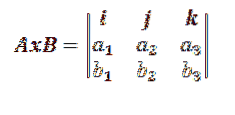
Kde i, j, k představují vektory, které tvoří základ R3.
Pomocí tohoto způsobu vyjádření křížového produktu máme, že předchozí příklad lze přepsat jako:
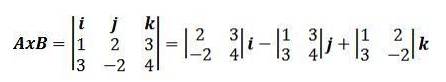
Vlastnosti
Některé vlastnosti, které má vektorový produkt, jsou následující:
Majetek 1
Pokud A je libovolný vektor v R.3, musíme:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Tyto vlastnosti lze snadno zkontrolovat pouze pomocí definice. Pokud A = (a1, a2, a3) máme:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Pokud i, j, k představují jednotkovou bázi R3, můžeme je napsat takto:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Takže máme, že následující vlastnosti jsou pravdivé:
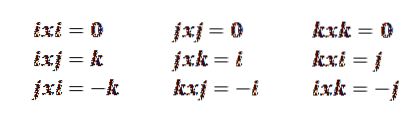
Jako mnemotechnické pravidlo se k zapamatování těchto vlastností často používá následující kruh:
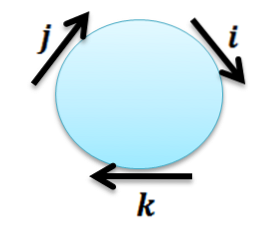
Zde musíme poznamenat, že jakýkoli vektor sám o sobě dává vektor 0 jako výsledek a zbytek produktů lze získat pomocí následujícího pravidla:
Křížový součin dvou po sobě jdoucích vektorů ve směru hodinových ručiček dává další vektor; a když se uvažuje proti směru hodinových ručiček, výsledkem je následující vektor se záporným znaménkem.
Díky těmto vlastnostem vidíme, že vektorový produkt není komutativní; například si všimněte, že i x j ≠ j x i. Následující vlastnost nám říká, jak AxB a BxA obecně souvisejí.
Nemovitost 2
Pokud jsou A a B vektory R3, musíme:
AxB = - (BxA).
Demonstrace
Pokud A = (a1, a2, a3) a B = (b1, b2, b3), podle definice externího produktu máme:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
Vidíme také, že tento produkt není asociativní s následujícím příkladem:
ix (ixj) = ixk = - j ale (ixi) xj = 0xj = 0
Z toho vidíme, že:
ix (ixj) ≠ (ixi) xj
Nemovitost 3
Pokud A, B, C jsou vektory R3 ar je reálné číslo, platí následující:
- Sekera (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Díky těmto vlastnostem můžeme vypočítat vektorový produkt pomocí zákonů algebry za předpokladu, že je respektováno pořadí. Například:
Pokud A = (1, 2, 3) a B = (3, -2, 4), můžeme je přepsat na základě kanonického základu R3.
Tedy A = i + 2j + 3k a B = 3i - 2j + 4k. Poté použijete předchozí vlastnosti:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) +12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Vlastnost 4 (produkt se třemi tečkami)
Jak jsme zmínili na začátku, kromě vektorového produktu existují i jiné způsoby, jak množit vektory. Jedním z těchto způsobů je skalární součin nebo vnitřní součin, který je označen jako A ∙ B a jehož definice je:
Pokud A = (a1, a2, a3) a B = (b1, b2, b3), pak A ∙ B = a1b1 + a2b2 + a3b3
Vlastnost, která se týká obou produktů, je známá jako trojitý skalární produkt.
Pokud jsou A, B a C vektory R3, pak A ∙ BxC = AxB ∙ C
Jako příklad se podívejme, že vzhledem k A = (1, 1, - 2), B = (- 3, 4, 2) a C = (- 5, 1, - 4) je tato vlastnost splněna.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
Na druhou stranu:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ∙ C = (10, 4, 7) ∙ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
Dalším trojitým produktem je Ax (BxC), který je známý jako trojitý vektorový produkt..
Vlastnost 5 (trojitý vektorový produkt)
Pokud jsou A, B a C vektory R3, pak:
Axe (BxC) = (A ∙ C) B - (A ∙ B) C
Jako příklad se podívejme, že vzhledem k A = (1, 1, - 2), B = (- 3, 4, 2) a C = (- 5, 1, - 4) je tato vlastnost splněna.
Z předchozího příkladu víme, že BxC = (- 18, - 22, 17). Pojďme vypočítat sekeru (BxC):
Sekera (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
Na druhou stranu musíme:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Musíme tedy:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Nemovitost 6
Je to jedna z geometrických vlastností vektorů. Pokud jsou A a B dva vektory v R3 a ϴ je úhel mezi nimi, pak:
|| AxB || = || A |||| B || sin (ϴ), kde || ∙ || označuje modul nebo velikost vektoru.
Geometrická interpretace této vlastnosti je následující:
Nechť A = PR a B = PQ. Pak úhel tvořený vektory A a B je úhel P trojúhelníku RQP, jak je znázorněno na následujícím obrázku.
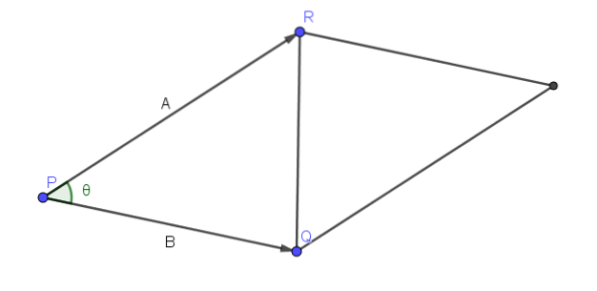
Proto je plocha rovnoběžníku, která má PR a PQ jako sousední strany, || A |||| B || sin (ϴ), protože můžeme brát jako základ || A || a jeho výška je dána || B || sin (ϴ).
Tím můžeme dojít k závěru, že || AxB || je oblast uvedeného rovnoběžníku.
Příklad
Vzhledem k následujícím vrcholům čtyřúhelníku P (1, -2,3), Q (4, 3, -1), R (2, 2,1) a S (5,7, -3) ukazují, že uvedený čtyřúhelník je rovnoběžník a najděte jeho oblast.
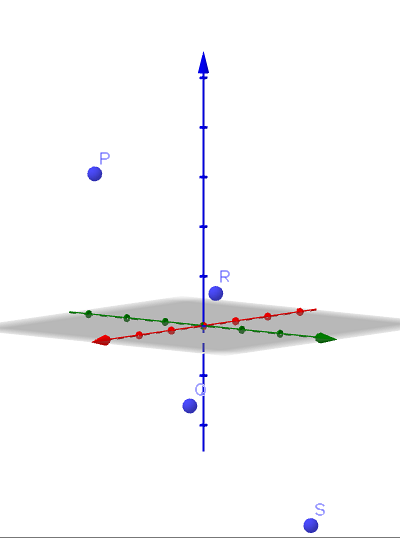
K tomu nejprve určíme vektory, které určují směr stran čtyřúhelníku. Tohle je:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
Jak vidíme, A a C mají stejný směrový vektor, takže máme, že oba jsou paralelní; totéž se děje s B a D. Proto jsme dospěli k závěru, že PQRS je rovnoběžník.
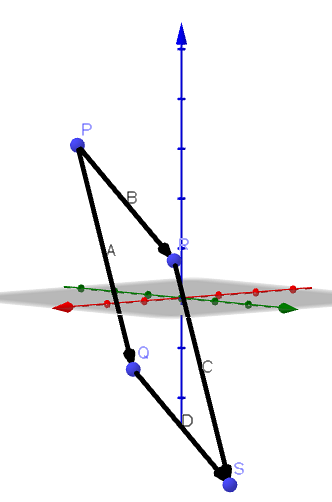
Abychom měli plochu tohoto rovnoběžníku, vypočítáme BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Plocha na druhou bude tedy:
|| BxA ||dva = (- 6)dva + (- dva)dva + (- 7)dva = 36 + 4 + 49 = 89.
Lze dojít k závěru, že plocha rovnoběžníku bude druhá odmocnina z 89.
Majetek 7
Dva vektory A a B jsou paralelní v R3 právě když AxB = 0
Demonstrace
Je jasné, že pokud A nebo B jsou nulový vektor, je splněno, že AxB = 0. Protože nulový vektor je rovnoběžný s jakýmkoli jiným vektorem, pak je vlastnost platná.
Pokud žádný z těchto dvou vektorů není nulovým vektorem, máme takové velikosti, že se liší od nuly; to znamená obě || A || ≠ 0 jako || B || ≠ 0, takže budeme mít || AxB || = 0 právě tehdy, když sin (ϴ) = 0, a to se stane právě tehdy, když ϴ = π nebo ϴ = 0.
Můžeme tedy uzavřít AxB = 0 právě tehdy, když ϴ = π nebo ϴ = 0, což se stane pouze tehdy, když jsou oba vektory navzájem paralelní.
Majetek 8
Pokud jsou A a B dva vektory v R3, pak AxB je kolmá na A i B..
Demonstrace
Pro tento důkaz si pamatujme, že dva vektory jsou kolmé, pokud je A ∙ B rovno nule. Dále víme, že:
A ∙ AxB = AxA ∙ B, ale AxA se rovná 0. Proto máme:
A ∙ AxB = 0 ∙ B = 0.
Tím můžeme dojít k závěru, že A a AxB jsou na sebe kolmé. Podobně musíme:
AxB ∙ B = A ∙ BxB.
Protože BxB = 0, máme:
AxB ∙ B = A ∙ 0 = 0.
Proto jsou AxB a B navzájem kolmé a s tím je vlastnost demonstrována. To je velmi užitečné, protože nám umožňuje určit rovnici roviny.
Příklad 1
Získejte rovnici roviny, která prochází body P (1, 3, 2), Q (3, - 2, 2) a R (2, 1, 3).
Nechť A = QR = (2 - 3,1 + 2, 3 - 2) a B = PR = (2 - 1,1 - 3, 3 - 2). Pak A = - i + 3j + k a B = i - 2j + k. Chcete-li najít rovinu tvořenou těmito třemi body, stačí najít vektor, který je kolmý k rovině, což je AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
S tímto vektorem a při použití bodu P (1, 3, 2) můžeme určit rovnici roviny následujícím způsobem:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Máme tedy, že rovnice roviny je 5x + 2y - z - 9 = 0.
Příklad 2
Najděte rovnici roviny, která obsahuje bod P (4, 0, - 2) a která je kolmá na každou z rovin x - y + z = 0 a 2x + y - 4z - 5 = 0 .
Víme, že normální vektor k rovině ax + by + cz + d = 0 je (a, b, c), máme, že (1, -1,1) je normální vektor x - y + z = 0 y (2,1, - 4) je normální vektor 2x + y - 4z - 5 = 0.
Normální vektor k hledané rovině proto musí být kolmý na (1, -1,1) a na (2, 1, - 4). Uvedený vektor je:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Pak máme, že hledaná rovina je ta, která obsahuje bod P (4,0, - 2) a má vektor (3,6,3) jako normální vektor.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Aplikace
Výpočet objemu rovnoběžnostěnu
Aplikace, která má trojitý skalární součin, má být schopna vypočítat objem rovnoběžnostěnu, jehož hrany jsou dány vektory A, B a C, jak je znázorněno na obrázku:
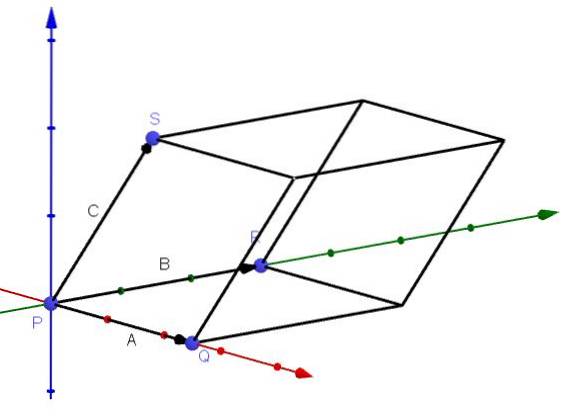
Tuto aplikaci můžeme odvodit následujícím způsobem: jak jsme již řekli, vektor AxB je vektor, který je kolmý k rovině A a B. Máme také, že vektor - (AxB) je další vektor kolmý k uvedené rovině.
Vybereme normální vektor, který tvoří nejmenší úhel s vektorem C; bez ztráty obecnosti nechť AxB je vektor, jehož úhel s C je nejmenší.
Máme, že AxB i C mají stejný výchozí bod. Dále víme, že plocha rovnoběžníku, která tvoří základ rovnoběžnostěnu, je || AxB ||. Pokud je tedy výška rovnoběžnostěnu dána h, máme, že jeho objem bude:
V = || AxB || h.
Na druhou stranu uvažujme skalární součin mezi AxB a C, který lze popsat následovně:
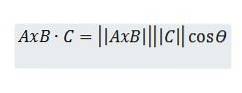
Podle trigonometrických vlastností však máme h = || C || cos (ϴ), takže máme:
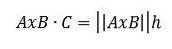
Tímto způsobem máme to:
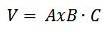
Obecně platí, že objem rovnoběžnostěnu je dán absolutní hodnotou trojitého skalárního součinu AxB ∙ C.
Vyřešená cvičení
Cvičení 1
Vzhledem k bodům P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) a S = (2, 6, 9) tvoří tyto body rovnoběžnostěn, jehož hrany jsou to PQ, PR a PS. Určete objem uvedeného rovnoběžnostěnu.
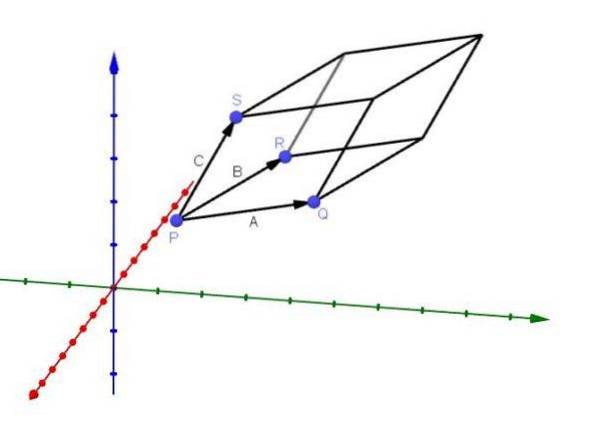
Řešení
Vezmeme-li:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
Pomocí vlastnosti trojitého skalárního součinu máme:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ∙ C = (8, -2, 20) ∙ (-3, 2, 2) = -24-4 +80 = 52.
Proto máme, že objem uvedeného rovnoběžnostěnu je 52.
Cvičení 2
Určete objem rovnoběžnostěnu, jehož hrany jsou dány A = PQ, B = PR a C = PS, kde body P, Q, R a S jsou (1, 3, 4), (3, 5, 3), (2, 1, 6) a (2, 2, 5).
Řešení
Nejprve máme A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Vypočítáme AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Poté vypočítáme AxB ∙ C:
AxB ∙ C = (2, -5, -6) ∙ (1, -1, 1) = 2 + 5 - 6 = 1.
Takže jsme dospěli k závěru, že objem uvedeného rovnoběžnostěnu je 1 kubická jednotka.
Reference
- Leithold, L. (1992). Výpočet s analytickou geometrií. HARLA, S.A..
- Resnick, R., Halliday, D., & Krane, K. (2001). Fyzika sv. 1. Mexiko: kontinentální.
- Saenz, J. (s.f.). Vektorový počet 1ed. Přepona.
- Spiegel, M. R. (2011). Vektorová analýza 2ed. Mc Graw Hill.
- Zill, D. G. a Wright, W. (2011). Výpočet několika proměnných 4ed. Mc Graw Hill.
Zatím žádné komentáře