
Rovnice koplanárních bodů, příklad a řešená cvičení
The koplanární body všichni patří do stejné roviny. Dva body jsou vždy koplanární, protože tyto body definují čáru, kterou procházejí nekonečné roviny. Oba body pak patří každé z rovin, které procházejí přímkou, a proto budou vždy koplanární.
Na druhou stranu tři body definují jednu rovinu, z čehož vyplývá, že tři body budou vždy koplanární s rovinou, kterou určují..
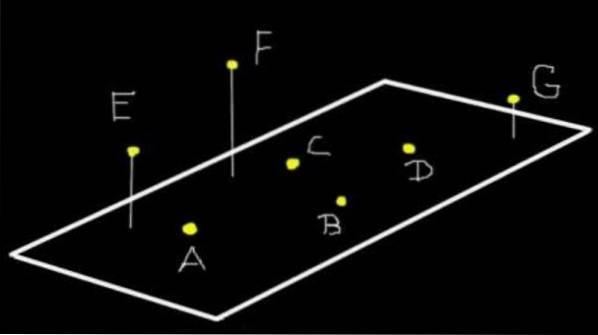
Více než tři body mohou být koplanární nebo ne. Například na obrázku 1 jsou body A, B, C a D koplanární k rovině (Ω). Ale E, F a G nejsou koplanární k (Ω), i když jsou koplanární k rovině, kterou definují.
Rejstřík článků
- 1 Rovnice roviny se třemi body
- 2 Příklad
- 2.1 Řešení
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 3.3 - Cvičení 3
- 3.4 - Cvičení 4
- 4 Odkazy
Rovnice roviny dané třemi body
Rovnice roviny určená třemi známými body A, B, C je matematický vztah, který zaručuje, že jakýkoli bod P s obecnými souřadnicemi (x, y, z), který splňuje rovnici, patří do uvedené roviny.
Předchozí výrok je ekvivalentní tvrzení, že pokud P souřadnic (x, y, z) splňuje rovnici roviny, bude uvedený bod koplanární se třemi body A, B, C, které určovaly rovinu.
Abychom našli rovnici této roviny, začněme hledáním vektorů AB Y AC:
AB = [Bx - Axe, By - Ay, Bz - Az]
AC = [Cx - Ax, Cy - Ay, Cz - Az]
Vektorový produkt AB X AC má za následek vektor kolmý nebo kolmý k rovině určený body A, B, C.
Jakýkoli bod P souřadnic (x, y, z) patří do roviny, pokud je vektor AP je kolmá na vektor AB X AC, což je zaručeno, pokud:
AP • (AB X AC) = 0
To odpovídá tvrzení, že trojitý produkt AP, AB Y AC je null. Výše uvedenou rovnici lze napsat v maticové formě:
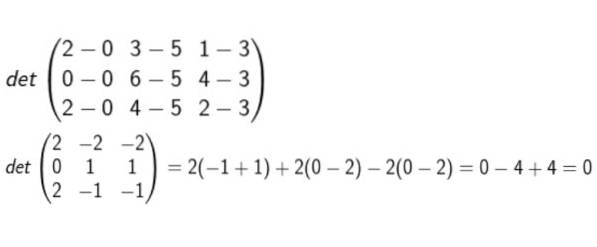
Příklad
Nechť body A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) a D (na, 0, 1). Jakou hodnotu by to mělo mít na takže čtyři body jsou koplanární?
Řešení
Chcete-li najít hodnotu a, musí být bod D součástí roviny určené A, B a C, což je zaručeno, pokud splňuje rovnici roviny.
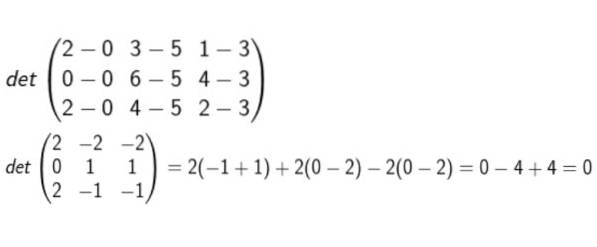
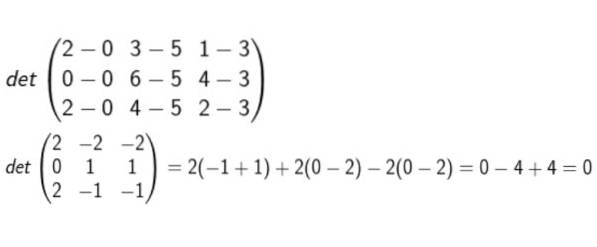
Rozvíjíme determinant, který máme:
a (-1-1) + 1 (-1 - 7) -1 (1 - 7) = -2a -8 + 6 = -2a - 2 = 0
To nám říká výše uvedená rovnice a = -1 aby byla rovnost naplněna. Jinými slovy, jediný způsob, jak ten bod D (na, 0,1) je koplanární s body A, B a C na hodnota -1. Jinak to nebude koplanární.
Vyřešená cvičení
- Cvičení 1
Rovina protíná karteziánské osy X, Y, Z v 1, 2 a 3. Průsečík této roviny s osami určuje body A, B a C. Najděte komponentu Dz bodu D, jehož kartézské komponenty jsou:
D (-Dz, Dz + 1, Dz)
Za předpokladu, že D je koplanární s body A, B a C.
Řešení
Jsou-li známy průsečíky roviny s kartézskými osami, lze použít segmentový tvar rovnice roviny:
x / 1 + y / 2 + z / 3 = 1
Protože bod D musí patřit do předchozí roviny, musí:
-Dz / 1 + (Dz + 1) / 2 + Dz / 3 = 1
A to:
-Dz + Dz / 2 + ½ + Dz / 3 = 1
Dz (-1 + ½ + ⅓) = ½
Dz (-1 / 6⅙) = ½
Dz = -3
Z výše uvedeného vyplývá, že bod D (3, -2, -3) je koplanární s body A (1, 0, 0); B (0, 2, 0) a C (0, 0, 3).
- Cvičení 2
Určete, zda body A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) a D (2, 3, 1) jsou koplanární.
Řešení
Tvoříme matici, jejíž řádky jsou souřadnice D-A, B-A a C-A. Poté se vypočítá determinant a ověří se, zda je či není nula.
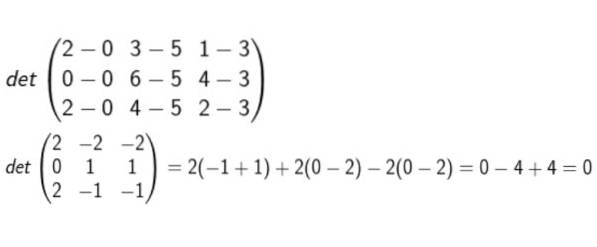
Po provedení všech výpočtů se dospělo k závěru, že jsou koplanární.
- Cvičení 3
V prostoru jsou dvě čáry. Jedním z nich je přímka (R), jejíž parametrická rovnice je:
(R): x = 1 + 2 λ; y = 1 - λ; z = 1
A druhá je přímka (S), jejíž rovnice je:
(S): x + 2 y = 1; z = -1
Ukažte, že (R) a (S) jsou koplanární čáry, to znamená, že leží ve stejné rovině.
Řešení
Začněme tím, že si libovolně vezmeme dva body na přímce (R) a dva na přímce (S):
Straight (R): λ = 0; A (1, 1, 1) a λ = 1; B (3, 0, 1)
Udělejme x = 0 na lince (S)=> y = ½; C (0, ½, -1). A na druhou stranu, pokud ano y = 0 => x = 1; D (1, 0, -1).
To znamená, že jsme vzali body A a B, které patří k přímce (R), a body C a D, které patří k přímce (S). Pokud jsou tyto body koplanární, budou také dvě linie koplanární.
Nyní jako bod otočení vybereme bod A a pak najdeme souřadnice vektorů AB, AC Y INZERÁT. Tímto způsobem získáte:
B - A: (3-1, 0-1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1; -1/2; -2)
D - A: (1-1, 0-1, -1 - 1) => INZERÁT= (0, -1, -2)
Dalším krokem je konstrukce a výpočet determinantu, jehož první řádek jsou koeficienty vektoru AB, druhá řada je z AC a třetí řádek vektoru INZERÁT:
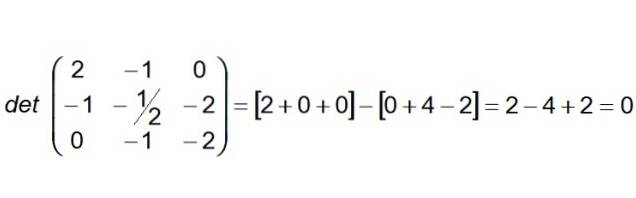
Protože se determinant ukáže jako nulový, můžeme usoudit, že čtyři body jsou koplanární. Dále lze konstatovat, že přímky (R) a (S) jsou také koplanární.
- Cvičení 4
Čáry (R) a (S) jsou koplanární, jak je ukázáno v cvičení 3. Najděte rovnici roviny, která je obsahuje.
Řešení
Body A, B, C tuto rovinu zcela definují, ale chceme vnucovat, že jakýkoli bod X souřadnic (x, y, z) patří do stejné.
X - A: (x-1, y-1, z-1) => SEKERA= (x-1, y-1, z - 1)
B - A: (3-1, 0-1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1; -1/2; -2)
Aby X patřilo do roviny definované A, B, C a ve které jsou obsaženy řádky (R) a (S), je nutné, aby determinant tvořený v jeho první řadě složkami SEKERA, ve druhém těmi z AB a ve třetím těmi z AC:
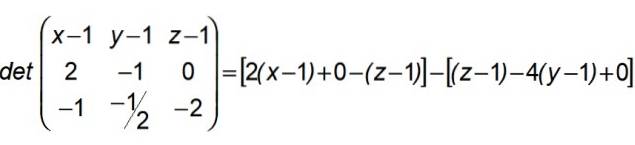
Po tomto výsledku se seskupíme tímto způsobem:
2 (x-1) + 4 (y-1) -2 (z-1) = 0
A hned uvidíte, že to lze přepsat takto:
x - 1 + 2y - 2 - z + 1 = 0
Proto x + 2y - z = 2 je rovnice roviny, která obsahuje přímky (R) a (S).
Reference
- Fleming, W. 1989. Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. 2006. Lineární algebra. Pearson Education.
- Leal, J. M. 2005. Rovinová analytická geometrie. Mérida - Venezuela: Redakční Venezolana C. A.
- Navarro, Rocio. Vektory. Obnoveno z: books.google.co.ve.
- Pérez, C. D. 2006. Předběžný výpočet. Pearson Education.
- Prenowitz, W. 2012. Základní pojmy geometrie. Rowman & Littlefield.
- Sullivan, M. 1997. Precalculus. Pearson Education.


Zatím žádné komentáře