
Koncept sítí Bravais, charakteristika, příklady, cvičení
The Bravaisovy sítě Jedná se o soubor čtrnácti trojrozměrných jednotkových buněk, ve kterých mohou být umístěny atomy krystalu. Tyto buňky se skládají z trojrozměrného uspořádání bodů, které tvoří základní strukturu, která se periodicky opakuje ve třech prostorových směrech..
Původ této nominální hodnoty pro základní krystalické struktury pochází z roku 1850, kdy Auguste Bravais ukázal, že existuje pouze 14 možných trojrozměrných buněk základní jednotky.

Sada 14 sítí Bravais je rozdělena do sedmi skupin nebo struktur podle geometrie buněk, těchto sedm skupin je:
1- Krychlový
2 - Tetragonální
3 - Ortorombická
4- Trigonal-Hexagonal
5- Monoklinické
6- Triclinic
7- Trigonální
Každá z těchto struktur definuje jednotkovou buňku, což je nejmenší část, která zachovává geometrické uspořádání atomů v krystalu..
Rejstřík článků
- 1 Charakteristika sítí Bravais
- 1.1 Kubické sítě
- 2 Příklady
- 2.1 - Železo
- 2.2 - Měď
- 2.3 - Drahé drahokamy
- 2.4 Topaz
- 3 Vyřešená cvičení
- 3.1 Cvičení 1
- 3.2 Cvičení 2
- 3.3 Cvičení 3
- 4 Odkazy
Charakteristika sítí Bravais
Čtrnáct sítí Bravais, jak bylo uvedeno výše, je rozděleno do sedmi skupin. Ale každá z těchto skupin má své jednotkové buňky se svými charakteristickými parametry, které jsou:
1- Síťový parametr (a, b, c)
2 - Počet atomů na buňku
3 - Vztah mezi síťovým parametrem a atomovým poloměrem
4 - Koordinační číslo
5- Faktor balení
6- intersticiální prostory
7- Prostřednictvím překladů podél vektorů a, b, c se opakuje krystalová struktura.
Kubické sítě
Skládá se z jednoduché kubické nebo kubické sítě P, kubické sítě se středem tváře nebo kubické sítě F a kubické sítě se středem těla nebo kubické sítě I.
Všechny kubické sítě mají všechny tři parametry sítě odpovídá směrům x, y, z stejné hodnoty:
a = b = c
Kubická síť P
Je třeba poznamenat, že atomy jsou reprezentovány koulemi, jejichž středy jsou na vrcholech kubické jednotkové buňky P.
V případě kubické mřížky P počet atomů na buňku je 1, protože v každém vrcholu je uvnitř jednotkové buňky pouze jedna osmina atomu, takže 8 * ⅛ = 1.
The koordinační číslo označuje počet atomů, které jsou blízkými sousedy v krystalové mřížce. V případě kubické mřížky P je koordinační číslo 6.
Kubická síť I
V tomto typu sítě je kromě atomů ve vrcholech krychle ve středu krychle také atom. Takže počet atomů na buňku jednotka v kubické mřížce P jsou 2 atomy.

Kubická síť F
Je to kubická mřížka, která má kromě atomů ve vrcholech také atom ve středu plochy každé krychle. The počet atomů na buňku je 4, protože každý ze šesti atomů obličeje má uvnitř buňky polovinu, tj. 6 * ½ = 3 plus 8 * ⅛ = 1 na vrcholech.

Šestihranná síť
V tomto případě je jednotkovou buňkou přímý hranol se šestihrannou základnou. Šestiúhelníkové sítě mají všechny tři parametry sítě odpovídající plnění následujícího vztahu:
a = b ≠ c
Úhel mezi vektorem a a b je 120 °, jak je znázorněno na obrázku. Zatímco mezi vektory a a c, stejně jako mezi b a c, jsou vytvářeny pravé úhly.

The počet atomů na buňku se vypočítá takto:
- V každé ze 2 bází hexagonálního hranolu je na šesti vrcholech 6 atomů. Každý z těchto atomů zaujímá ⅙ jednotkové buňky.
- Ve středu každé ze 2 hexagonálních bází je 1 atom, který zabírá 1/2 jednotkové buňky.
- Na 6 postranních stranách hexagonálního hranolu jsou 3 atomy, z nichž každý zaujímá unit jednotkové buňky a 3 atomy, přičemž každý zaujímá ⅓ objemu jednotkové buňky.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
Vztah mezi parametry mřížky aab s atomovým poloměrem R za předpokladu, že všechny atomy mají stejný poloměr a jsou v kontaktu, je:
a / R = b / R = 2
Příklady
Kovy jsou hlavními příklady krystalických struktur a také nejjednoduššími, protože se obvykle skládají pouze z jednoho typu atomu. Existují však i jiné nekovové sloučeniny, které také tvoří krystalické struktury, jako je diamant, křemen a mnoho dalších..
- Železo
Železo má jedinou kubickou jednotkovou buňku s mřížkovým nebo okrajovým parametrem a = 0,297 nm. V 1 mm jsou 3,48 x 10 ^ 6 jednotkových buněk.
- Měď
Má kubickou krystalickou strukturu zaměřenou na obličej, která je tvořena výhradně atomy mědi..
- Drahé drahokamy
Drahé drahokamy jsou krystalické struktury v podstatě ze stejné sloučeniny, ale s malými částmi nečistot, které jsou často zodpovědné za jejich barvu..
diamant
Je složen výhradně z uhlíku a neobsahuje nečistoty, a proto je bezbarvý. Diamant má krychlová krystalová struktura (isometric-hexoctahedral) and is the mostest known material.
Křemen
Skládá se z oxidu křemičitého, je obecně bezbarvý nebo bílý. Jeho krystalická struktura je trigonálně-lichoběžníková.
Rubín
Skládá se z oxidu hlinitého s nečistotami chrómu, které mu dodávají charakteristickou červenou barvu. Formulář a šestihranná krystalová mříž.
Safír
Je to také krystal oxidu hlinitého, ale s nečistotami titanu a železa, které jsou zodpovědné za jeho modrou barvu v různých odstínech. Jako má rubín šestihranná struktura.
Nefrit
Drahokam obecně zelené barvy, má monoklinická struktura a skládá se z křemičitanu železo-hořečnato-vápenatého.
Topas
Je bezbarvý s a ortorombická struktura fluorid-hydroxid-křemičitan hlinitý.
Vyřešená cvičení
Cvičení 1
Najděte vztah mezi parametrem mřížky a poloměrem atomu pro kubickou mřížku F..
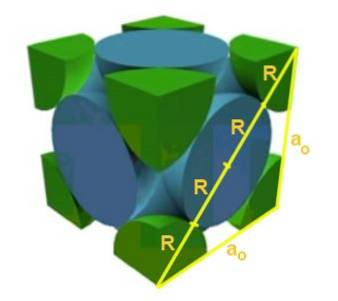
Řešení: Nejprve se předpokládá, že atomy jsou reprezentovány jako koule o celém poloměru R ve vzájemném "kontaktu", jak je znázorněno na obrázku. Vznikne pravý trojúhelník, ve kterém platí, že:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Proto je vztah mezi hranou a poloměrem:
a / R = 4 / √2
Cvičení 2
Najděte vztah mezi parametrem mřížky a poloměrem atomu pro kubickou mřížku I (střed těla).
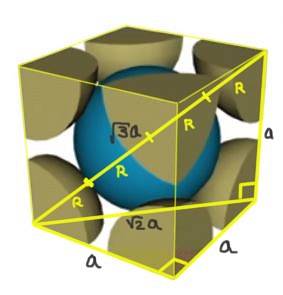
Řešení: Atomy mají být reprezentovány jako koule o celém poloměru R ve vzájemném "kontaktu", jak je znázorněno na obrázku.
Jsou vytvořeny dva pravé trojúhelníky, jeden z přepony √2a a druhý z přepony √3a, jak lze dokázat pomocí Pythagorovy věty. Odtud vyplývá, že vztah mezi parametrem mřížky a poloměrem atomu pro kubickou mřížku I (se středem v těle) je:
a / R = 4 / √3
Cvičení 3
Najděte faktor balení F pro jednotkovou buňku kubické struktury F (kubický střed), ve které mají atomy poloměr R a jsou v „kontaktu“.
Řešení: Faktor balení F je definován jako podíl mezi objemem obsazeným atomy v jednotkové buňce a objemem buňky:
F = Vatomy / Vbuňka
Jak je uvedeno výše, počet atomů na jednotku buňky v kubické mřížce se středem tváře je 4, takže faktor balení bude:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Reference
- Centrum akademických zdrojů krystalických struktur. [PDF]. Citováno dne 24. května 2018 z: web.iit.edu
- Krystaly. Citováno dne 26. května 2018 z: thoughtco.com
- Tiskové knihy. 10.6 Mřížkové struktury v krystalických tělesech. Citováno dne 26. května 2018 z: opentextbc.ca
- Ming. (2015, 30. června). Typy krystalových struktur. Citováno dne 26. května 2018 z: crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31. ledna 2018). Typy
- Kittel Charles (2013) Fyzika pevných látek, Fyzika kondenzovaných látek (8. vydání). Wiley.
- KHI. (2007). Krystalické struktury. Citováno dne 26. května 2018 z: folk.ntnu.no
- Wikipedia. Bravais svazy. Obnoveno z: en.wikipedia.com.



Zatím žádné komentáře