Pravidlo první ruky a druhé pravidlo, aplikace, cvičení

The pravidlo pravé ruky je mnemotechnický prostředek k určení směru a smyslu vektoru, který je výsledkem vektorového produktu nebo křížového produktu. Je široce používán ve fyzice, protože existují důležité vektorové veličiny, které jsou výsledkem vektorového produktu. Tak je tomu například v případě točivého momentu, magnetické síly, momentu hybnosti a magnetického momentu.

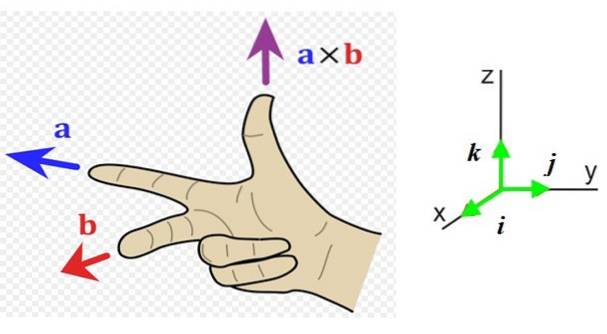
Dovolit být dva obecné vektory na Y b jehož křížový produkt je na X b. Modul takového vektoru je:

na X b = a.b. v α

Kde α je minimální úhel mezi na Y b, zatímco a a b představují jeho moduly. K rozlišení vektorů jejich modulů se používají tučná písmena.

Nyní potřebujeme znát směr a smysl tohoto vektoru, takže je vhodné mít referenční systém se třemi směry prostoru (obrázek 1 vpravo). Jednotkové vektory i, j Y k míří příslušně na čtenáře (mimo stránku), doprava a nahoru.

V příkladu na obrázku 1 vlevo vektor na míří doleva (směr Y minus a ukazováček pravé ruky) a vektor b jde ke čtenáři (směr X pozitivní, prostředníček pravé ruky).

Výsledný vektor na X b má palec ve směru nahoru z pozitivní.

Rejstřík článků

• 1 Druhé pravidlo pravé ruky
  • 1.1 Alternativní pravidlo pravé ruky
• 2 Aplikace
  • 2.1 Úhlová rychlost a zrychlení
  • 2.2 Moment hybnosti
• 3 cvičení
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
• 4 Odkazy

Druhé pravidlo pravé ruky

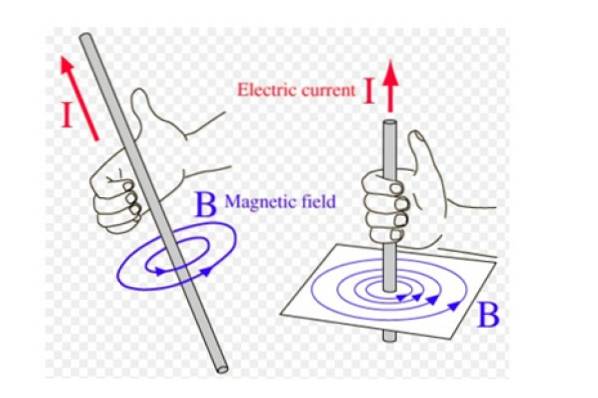
Toto pravidlo se také nazývá pravidlo pravého palce, Hodně se používá, když existují veličiny, jejichž směr a směr se otáčejí, například magnetické pole B tenkým přímým vodičem, který nese proud.

V tomto případě jsou magnetické siločáry soustředné kružnice s drátem a směr otáčení se získá tímto pravidlem následujícím způsobem: pravý palec ukazuje ve směru proudu a zbývající čtyři prsty jsou zakřivené ve směru venkov. Koncept ilustrujeme na obrázku 2.

Alternativní pravidlo pravé ruky

Obrázek níže ukazuje alternativní formu pravidla pro pravou ruku. Vektory, které se objevují na obrázku, jsou:

-Rychlost proti bodového náboje q.

-Magnetické pole B ve kterém se zatížení pohybuje.

-F_B síla, kterou magnetické pole působí na náboj.

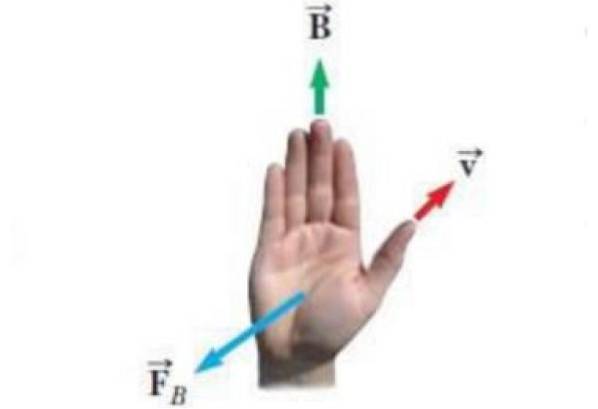
Rovnice pro magnetickou sílu je F_B = qproti X B a pravidlem pravé ruky znát směr a smysl pro F_B se použije takto: palec ukazuje podle v, čtyři zbývající prsty se umístí podle pole B. Potom F_B je vektor, který vychází z dlaně ruky, kolmo na ni, jako by tlačil na zátěž.

Všimněte si, že F_B Ukázal bych opačným směrem pokud byl náboj q záporný, protože vektorový produkt není komutativní. Ve skutečnosti:

na X b = - b X na

Aplikace

Pravidlo pravé ruky lze použít pro různé fyzikální veličiny, některé z nich si povíme:

Úhlová rychlost a zrychlení

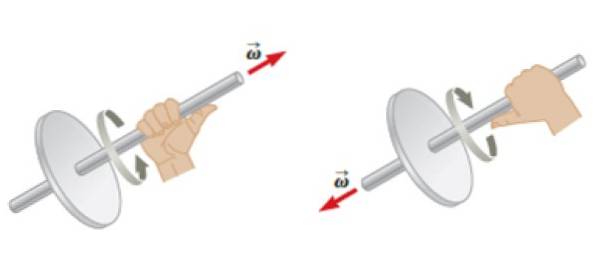
Obě úhlové rychlosti ω jako úhlové zrychlení α jsou to vektory. Pokud se objekt otáčí kolem pevné osy, je možné přiřadit směr a smysl těchto vektorů pomocí pravidla pravé ruky: čtyři prsty jsou zvlněné po rotaci a palec okamžitě nabízí směr a smysl úhlové rychlosti ω.

Úhlové zrychlení α bude mít stejnou adresu jako ω, ale jeho význam závisí na tom, zda ω se časem zvyšuje nebo snižuje. V prvním případě mají oba stejný směr a smysl, ale ve druhém budou mít opačné směry..

Moment hybnosti

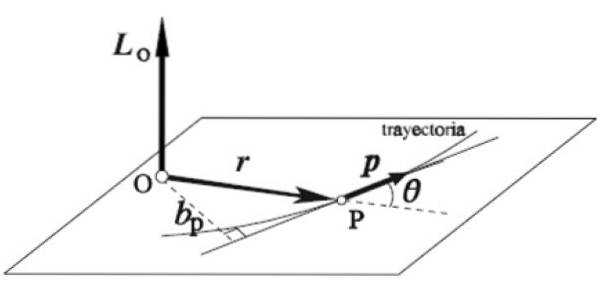
Vektor momentu hybnosti L_NEBO částice, která se otáčí kolem určité osy O, je definována jako vektorový produkt jejího vektoru okamžité polohy r  a lineární hybnost p:

L = r X p

Pravidlo pravé ruky se uplatňuje tímto způsobem: ukazováček je umístěn ve stejném směru a smyslu r, prostředníček na p, oba ve vodorovné rovině, jako na obrázku. Palec se automaticky vysune svisle nahoru, což naznačuje směr a smysl momentu hybnosti L_NEBO.

Výcvik

- Cvičení 1

Vrchol na obrázku 6 se rychle otáčí s úhlovou rychlostí ω a jeho osa symetrie se otáčí pomaleji kolem svislé osy z. Tento pohyb se nazývá precese. Popište síly působící na rotující vršek a účinek, který produkují.

Řešení

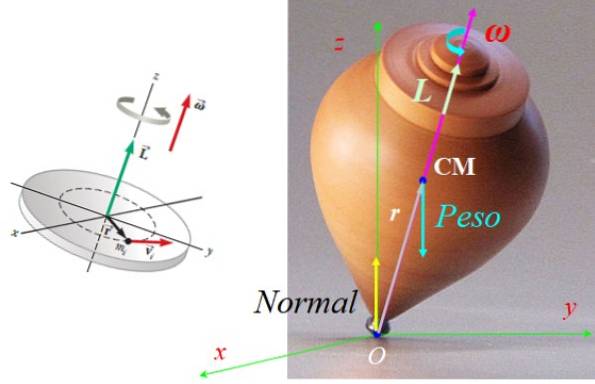
Síly působící na vrchol jsou normální N, aplikován na otočný bod se zemí O plus váha M.G, aplikován ve středu hmoty CM, s G gravitační vektor zrychlení, směrovaný svisle dolů (viz obrázek 7).

Obě síly se vyrovnávají, proto se vrchol nepohybuje. Hmotnost však vytváří točivý moment nebo točivý moment τ síť vzhledem k bodu O danému:

τ_NEBO = r_NEBO X F, s F = MG.

Co r a M.G jsou vždy ve stejné rovině, jak se otáčí vršek, podle pravidla pravé ruky točivý moment τ_NEBO se vždy nachází v letadle xy, kolmo na oba r Co G.

Všimněte si, že N neprodukuje točivý moment vzhledem k O, protože jeho vektor r s ohledem na O je null. Tento točivý moment vytváří změnu momentu hybnosti, která způsobí, že vrchol předchází kolem osy Z..

- Cvičení 2

Uveďte směr a smysl vektoru momentu hybnosti L horní části obrázku 6.

Řešení

Jakýkoli bod na vrcholu má hmotnost m_i, rychlost proti_i a polohový vektor r_i, když se otáčí kolem osy z. Moment hybnosti L_i uvedené částice je:

L_i = r_i X p_i = r_i x m_iproti_i

Vzhledem k r_i Y proti_i jsou kolmé, velikost L to je:

L_i = m_ir_iproti_i

Lineární rychlost proti souvisí s úhlovou rychlostí ω přes:

proti_i = r_iω

Proto:

L_i = m_ir_i (r_iω) = m_ir_i^dvaω

Celkový moment hybnosti rotujícího vršku L je součtem momentu hybnosti každé částice:

L = (∑m_ir_i^dva ) ω

∑ m_ir_i^dva  je moment setrvačnosti I vrcholu, pak:

L= Jáω

Proto L Y ω mají stejný směr a smysl, jak je znázorněno na obrázku 7.

Reference

1. Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill. 
2. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
3. Kirkpatrick, L. 2007. Fyzika: Pohled na svět. 6. zkrácené vydání. Cengage Learning.
4. Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson. 
5. Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1 a 2. 7.. Ed. Cengage Learning.