
Simpsonův vzorec pravidla, důkaz, příklady, cvičení
The Simpsonovo pravidlo je metoda výpočtu přibližným způsobem určitých integrálů. Je založen na rozdělení integračního intervalu na sudý počet rovnoměrně rozmístěných dílčích intervalů.
Extrémní hodnoty dvou po sobě jdoucích dílčích intervalů definují tři body, kterými se parabola, jejíž rovnice je polynom druhého stupně, hodí.
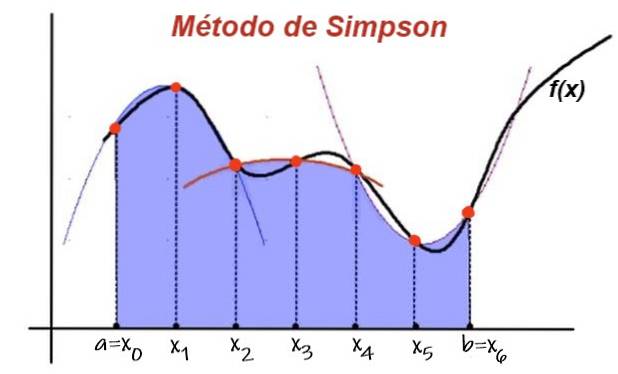
Poté se plocha pod křivkou funkce ve dvou po sobě jdoucích intervalech aproximuje oblastí interpolačního polynomu. Přidáním příspěvku do oblasti pod parabolou všech po sobě jdoucích dílčích intervalů máme přibližnou hodnotu integrálu.
Na druhou stranu, protože integrál paraboly lze vypočítat algebraicky přesně, je možné najít analytický vzorec pro přibližnou hodnotu určitého integrálu. To je známé jako Simpsonův vzorec.
Chyba takto získaného přibližného výsledku klesá, protože počet dělení n je větší (kde n je sudé číslo).
Níže bude uveden výraz, který umožňuje odhadnout horní mez chyby aproximace na integrál I, když byla vytvořena část n pravidelných podintervalů celkového intervalu [a, b].
Rejstřík článků
- 1 vzorec
- 2 Demo
- 2.1 Koeficienty interpolačního polynomu
- 2.2 Výpočet přibližného integrálu v [Xi, Xi + 2]
- 2.3 Přibližný výpočet integrálu v [a, b]
- 2.4 Chyba aproximace
- 3 Pracované příklady
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 3.3 - Příklad 3
- 4 Navrhované cvičení
- 5 Reference
Vzorec
Integrační interval [a, b] je rozdělen na n podintervalů, kde n je sudé celé číslo. Šířka každého pododdělení bude:
h = (b - a) / n
Tímto způsobem se v intervalu [a, b] vytvoří oddíl:
X0, X1, X2,…, Xn-1, Xn
Kde X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
Vzorec, který umožňuje přibližným způsobem vypočítat určitý integrál I spojité a nejlépe hladké funkce na intervalu [a, b] je:
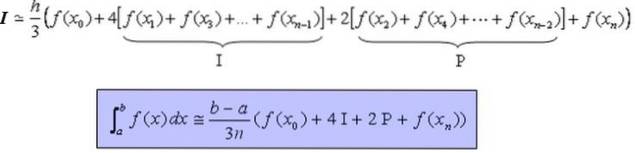
Demonstrace
Pro získání Simpsonova vzorce je v každém podintervalu [Xi, Xi + 2] aproximována funkce f (X) polynomem druhého stupně p (X) (parabola), který prochází třemi body: [Xi, f (Xi)] ; [Xi + 1, f (Xi + 1)] a [Xi + 2, f (Xi + 2)].
Potom spočítáme integrál polynomu p (x) v [Xi, Xi + 2], který aproximuje integrál funkce f (X) v tomto intervalu.
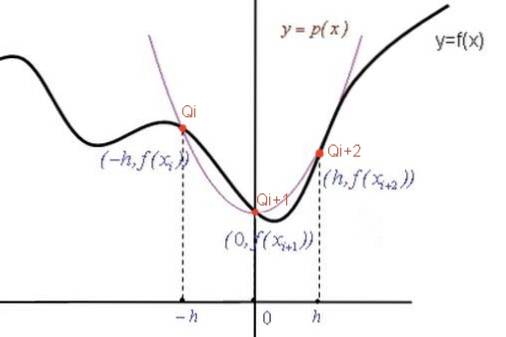
Koeficienty interpolačního polynomu
Rovnice paraboly p (X) má obecný tvar: p (X) = A Xdva + B X + C. Když parabola prochází červeně označenými body Q (viz obrázek), pak se koeficienty A, B, C stanoví z následujícího systému rovnic:
A (-h)dva - B h + C = f (Xi)
C = f (Xi + 1)
A (h)dva + B h + C = f (Xi + 2)
Je vidět, že je určen koeficient C. Pro určení koeficientu A přidáme první a třetí rovnici získáním:
2 A hdva + 2 C = f (Xi) + f (Xi + 2).
Pak je hodnota C nahrazena a A je vymazána, takže:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hdva)
K určení koeficientu B se třetí rovnice odečte od první a B se vyřeší a získá se:
B = [f (Xi + 2) - f (Xi)] = 2 hodiny.
Stručně řečeno, polynom druhého stupně p (X), který prochází body Qi, Qi + 1 a Qi + 2, má koeficienty:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hdva)
B = [f (Xi + 2) - f (Xi)] = 2 h
C = f (Xi + 1)
Výpočet přibližného integrálu v [Xi, Xi + 2]
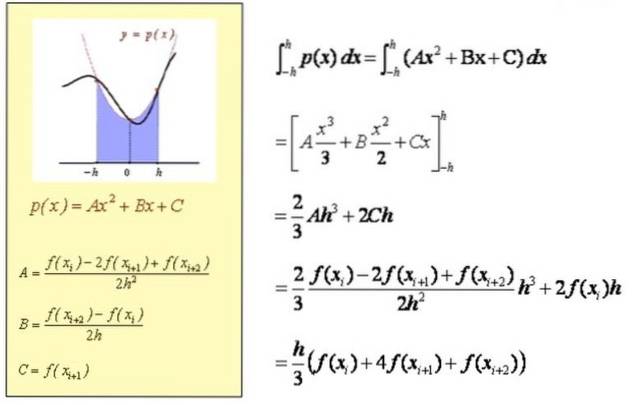
Přibližný výpočet integrálu v [a, b]
Jak již bylo zmíněno, na celkovém integračním intervalu [a, b] se vytvoří oddíl X0, X1, X2,…, Xn-1, Xn s krokem h = Xi + 1 - Xi = (b - a) / n , kde n je sudé číslo.
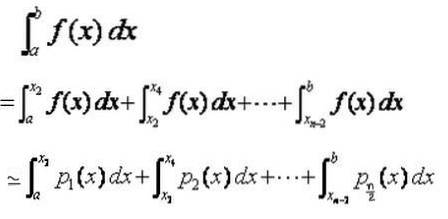
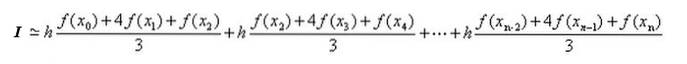
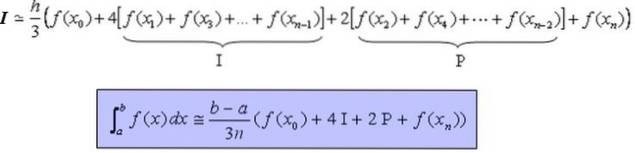
Chyba aproximace
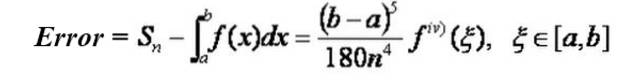
Všimněte si, že chyba klesá se čtvrtým výkonem počtu dělení v intervalu. Například pokud přejdete z n pododdělení na 2n, pak se chyba sníží o faktor 1/16.
Horní mez chyby získané pomocí Simpsonovy aproximace lze získat ze stejného vzorce nahrazením maximální absolutní hodnoty čtvrté derivace v intervalu [a, b] čtvrtou derivací.
Pracoval příklady
- Příklad 1
Uvažujme funkci o funkci f (X) = 1 / (1 + Xdva).
Najděte konečný integrál funkce f (X) na intervalu [-1, 1] pomocí Simpsonovy metody se dvěma děleními (n = 2).
Řešení
Bereme n = 2. Limity integrace jsou a = -1 a b = -2, takže oddíl vypadá takto:
X ° = -1; X1 = 0 a X2 = +1.
Proto má Simpsonův vzorec následující podobu:

S n = 2 → xo = -1, x1 = 0; x2 = 1, proto:

- Příklad 2
Uvažujme funkci f (X) = 1 / (1 + Xdva).
Najděte konečný integrál funkce f (X) na intervalu [-1, 1] pomocí Simpsonova vzorce se čtyřmi děleními (n = 4).
Řešení
Bereme n = 4. Limity integrace jsou a = -1 a b = -2, takže oddíl vypadá takto:
X ° = -1; X1 = -1/2; X2 = 0; X3 = 1/2 a X4 = +1.
Simpsonův vzorec je uveden takto:
Integrální ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
V případě, že se aplikuje, je to následující:
Integrální ≃ (1 - (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)
Integrální ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666
- Příklad 3
Určete přesně určitý integrál předchozích příkladů a proveďte srovnání přesného výsledku s výsledky získanými pomocí Simpsonova vzorce v příkladech 1a a 1b.
Řešení
Neurčitý integrál funkce f (X) = 1 / (1 + Xdva) je funkce arktan (X).
Při hodnocení v mezích integrace zůstává:
Integrál = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1,5708
Pokud porovnáme výsledek přesného řešení s výsledkem získaným Simpsonovou metodou s n = 2 an = 4, máme:
Pro n = 2 je rozdíl mezi přesným a přibližným řešením π / 2 - 5/3 = -0,0959, to znamená procentuální rozdíl -0,06%.
A pro Simpsonovu aproximaci s n = 4 je rozdíl mezi přesným a přibližným řešením π / 2 - 47/30 = 0,0041, to znamená procentuální rozdíl 0,003%.
Navrhované cvičení
Simpsonova metoda je vhodná pro použití v programovacích jazycích a v počítačových aplikacích pro matematické výpočty. Navrhuje se, aby čtenář na základě vzorců uvedených v tomto článku napsal svůj vlastní kód do svého oblíbeného programu.
Následující obrázek ukazuje cvičení, ve kterém byl Simpsonův vzorec implementován Smath studio, zdarma dostupný software pro operační systémy Okna Y Android.

Reference
- Casteleiro, J. M. 2002. Integrální počet (ilustrované vydání). Madrid: ESIC Editorial.
- UPV. Simpsonova metoda. Polytechnická univerzita ve Valencii. Obnoveno z: youtube.com
- Purcell, E. 2007. Deváté vydání kalkulu. Hala Prentice.
- Wikipedia. Simpsonovo pravidlo. Obnoveno z: es.wikipedia.com
- Wikipedia. Lagrangeova polynomiální interpolace. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře