The matematický vztah je spojení, které existuje mezi prvky podmnožiny s ohledem na součin dvou sad. A funkce zahrnuje matematickou operaci k určení hodnoty závislé proměnné na základě hodnoty nezávislé proměnné. Každá funkce je relací, ale ne každý vztah je funkcí.
| Vztah | Funkce | |
|---|---|---|
| Definice | Podmnožina seřazených párů, které odpovídají karteziánskému součinu dvou sad. | Matematická operace, která má být provedena s proměnnou X získat proměnnou Y. |
| Zápis | X R Y; X to souvisí s Y. | Y= ƒ (X); Y je funkce X. |
| Vlastnosti |
|
|
| Příklady |
|
|
Říká se tomu binární vztah množiny A v množině B nebo vztah mezi prvky A a B ke každé podmnožině C kartézského součinu A x B.
To znamená, že pokud množinu A tvoří prvky 1, 2 a 3 a množinu B tvoří prvky 4 a 5, kartézský součin A x B budou uspořádané páry:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Podmnožina C = (2,4), (3,5) bude vztahem A a B, protože se skládá z uspořádaných párů (2,4) a (3, 5), což je výsledek karteziánské produkt A x B.
„Nechť A a B jsou libovolné dvě neprázdné množiny, ať A x B je množina součinů obou, to znamená: A x B je tvořeno uspořádanými páry (x, y) tak, že X je prvek A a Y je pro B. Pokud je libovolná podmnožina C definována v A x B, binární relace v A a B se automaticky určí takto:
X R Y právě když (x, y)) C
(notace X R Y Prostředky "X to souvisí s Y").
Zavoláme množinu A. počáteční sada a zavoláme množinu B přílet nastaven.
The vztahová doména jsou prvky, které tvoří výchozí sadu, zatímco rozsah poměru jsou prvky sady příjezdu.
Soubor NA z X prvků mužů v populaci a B je množina Y prvky žen ze stejné populace. Vztah je navázán, když „X je ženatý Y".
Když mluvíme o matematické funkci množiny A v množině B, odkazujeme na pravidlo nebo mechanismus, který spojuje prvky množiny A s prvkem množiny B.
„Sean X Y Y dvě skutečné proměnné, pak se říká, že y je funkce x ano každé hodnotě, kterou beru X odpovídá hodnotě Y."
Nezávislá proměnná je X zatímco Y je závislá proměnná nebo funkce:
y = ƒ (x)
Soubor, ve kterém X to se nazývá doména funkce (originál) a variace Y rozsah funkcí (obrázek).
Sada párů (X, Y) takové, že Y= ƒ (X) je nazýván funkční graf; pokud jsou zastoupeny v kartézských osách, získá se rodina bodů zvaná funkční graf.
V matematice získáme mnoho příkladů funkcí. Zde jsou příklady hlavních funkcí.
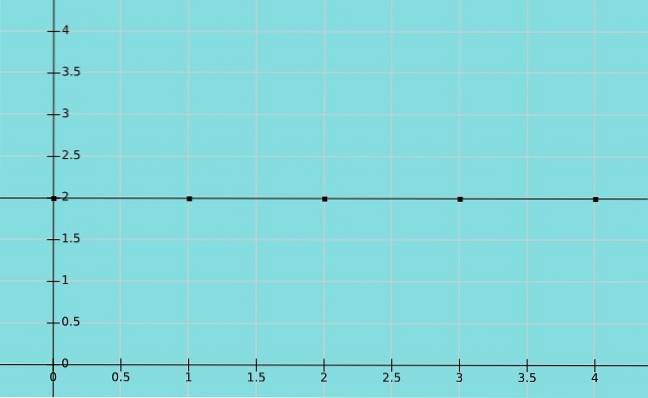
Funkce se nazývá konstantní, pokud je prvek množiny B, který odpovídá množině A, stejný. V tomto případě všechny hodnoty x odpovídají stejné hodnotě y. Doménou jsou tedy reálná čísla, zatímco rozsah je konstantní hodnotou.
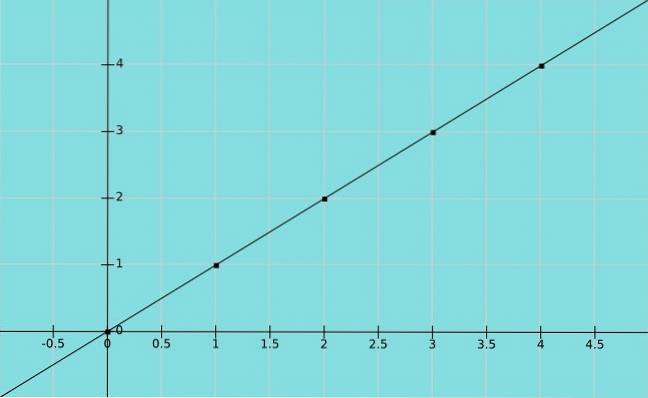
Předpokládejme X je proměnná a to Y má stejnou hodnotu jako X. Pak máme funkci identity y = x, kde páryx, y) v grafu jsou (1,1), (2,2), (3,3) atd.
Polynomiální funkce plní tvar y = anXn+nan-1+Xn-1+… + AdvaXdva+na1x + a0. Výše uvedený graf ukazuje funkci ƒ (x) = xdva+x-2.
Nyní předpokládejme, že závislá proměnná Y se rovná nezávislé proměnné X zvednutý ke kostce. Máme funkci y = x3, jehož graf je zobrazen níže:
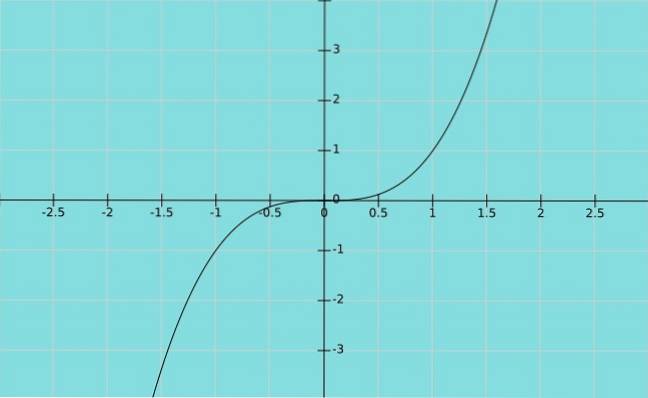
Zatím žádné komentáře