Půlkruh, jak vypočítat obvod, plochu, těžiště, cvičení

The půlkruh je rovinný údaj ohraničený průměrem obvodu a jedním ze dvou plochých kruhových oblouků určených uvedeným průměrem.

Tímto způsobem je půlkruh ohraničen a půlkruh, který se skládá z plochého kruhového oblouku a přímého segmentu, který spojuje konce plochého kruhového oblouku. Půlkruh obklopuje půlkruh a všechny body v něm..

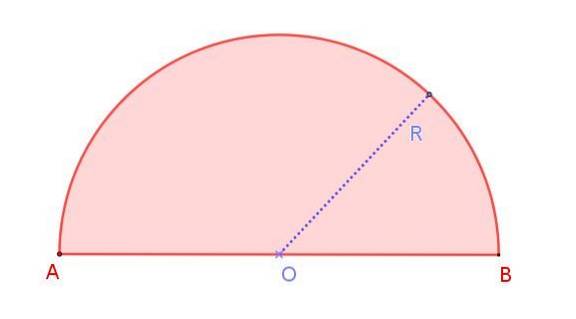
Vidíme to na obrázku 1, který ukazuje půlkruh o poloměru R, jehož míra je poloviční oproti průměru AB. Všimněte si, že na rozdíl od kruhu, ve kterém jsou nekonečné průměry, je v půlkruhu pouze jeden průměr.

Půlkruh je geometrický útvar s mnoha využitími v architektuře a designu, jak vidíme na následujícím obrázku:

Rejstřík článků

• 1 Prvky a míry půlkruhu
  • 1.1 Obvod půlkruhu
  • 1.2 Plocha půlkruhu
  • 1.3 Těžiště půlkruhu
  • 1.4 Moment setrvačnosti půlkruhu
  • 1.5 Vepsaný úhel
• 2 Vyřešená cvičení
  • 2.1 Cvičení 1 
  • 2.2 Cvičení 2
  • 2.3 Cvičení 3
  • 2.4 Cvičení 4
  • 2.5 Cvičení 5
• 3 Odkazy

Prvky a míry půlkruhu

Prvky půlkruhu jsou:

1. - Rovinný kruhový oblouk A⌒B

2. - Segment [AB] 

3.- Body uvnitř půlkruhu složené z oblouku A⌒B a segmentu [AB].

Obvod půlkruhu

Obvod je součtem kontury oblouku plus kontury přímého segmentu, proto:

Obvod = délka oblouku A⌒B + délka segmentu [AB]

V případě půlkruhu o poloměru R bude jeho obvod P dán vzorcem:

P = π⋅R + 2⋅R = (π + 2) ⋅R

První člen je polovina obvodu kruhu o poloměru R, zatímco druhý je délka průměru, což je dvojnásobek poloměru..

Plocha půlkruhu

Vzhledem k tomu, že půlkruh je jedním z rovinných úhlových sektorů, které zůstávají při kreslení průměru přes obvod, jeho oblast A bude polovinou oblasti kruhu, který obsahuje půlkruh o poloměru R:

A = (π⋅R^dva) / 2 = ½ π⋅R^dva

Těžiště půlkruhu

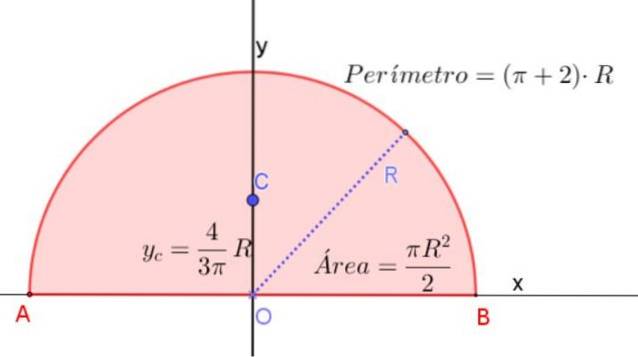
Těžiště půlkruhu je na jeho ose symetrie ve výšce měřené od jeho průměru 4 / (3π) krát poloměru R.

To odpovídá přibližně 0,424⋅R, měřeno od středu půlkruhu a na jeho ose symetrie, jak je znázorněno na obrázku 3.

Moment setrvačnosti půlkruhu

Moment setrvačnosti rovinného útvaru vzhledem k ose, například k ose x, je definován jako:

Integrál čtverce vzdálenosti bodů patřících k obrázku k ose, přičemž integrační rozdíl je nekonečně malým prvkem plochy, zaujatý v poloze každého bodu. 

Obrázek 4 ukazuje definici momentu setrvačnosti I_X půlkruhu o poloměru R, vzhledem k ose X, která prochází jeho úhlopříčkou:

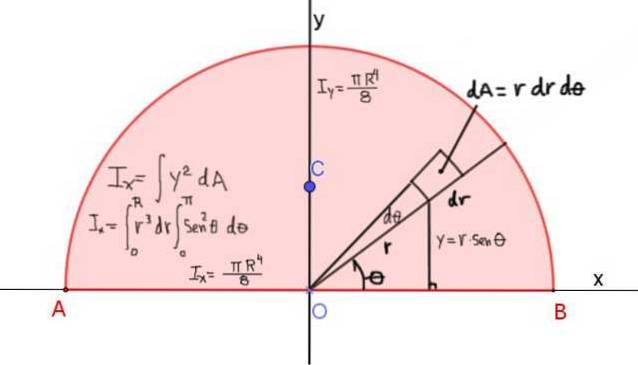
Moment setrvačnosti kolem osy x je dán vztahem:

Já_X = (π⋅R⁴) / 8

A moment setrvačnosti vzhledem k ose symetrie y je:

Iy = (π⋅R⁴) / 8

Je třeba poznamenat, že oba momenty setrvačnosti se shodují v jejich vzorci, ale je důležité si uvědomit, že odkazují na různé osy.

Vepsaný úhel

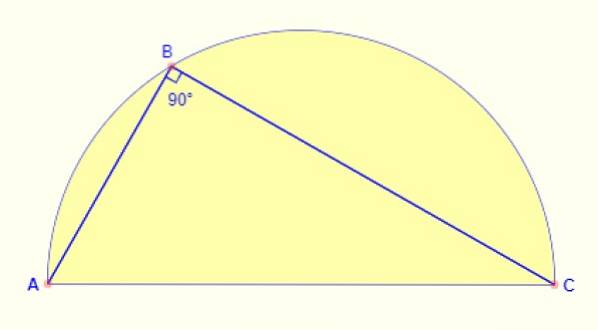
Úhel zapsaný do půlkruhu je vždy 90 °. Bez ohledu na to, kde je bod zachycen na oblouku, je úhel mezi stranami AB a BC obrázku vždy pravý..

Vyřešená cvičení

Cvičení 1 

Určete obvod půlkruhu o poloměru 10 cm.

Řešení

Nezapomeňte, že obvod jako funkce poloměru je dán vzorcem, který jsme viděli dříve:

P = (2 + π) ⋅R

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Cvičení 2

Najděte plochu půlkruhu o poloměru 10 cm.

Řešení

Vzorec pro plochu půlkruhu je:

A = ½ π⋅R^dva = ½ π⋅ (10 cm)^dva = 50π cm^dva = 50 x 3,14 cm^dva = 157 cm^dva.

Cvičení 3

Určete výšku h těžiště půlkruhu o poloměru R = 10 cm, měřeno od jeho základny, přičemž průměr půlkruhu je stejný. 

Řešení

Těžiště je rovnovážným bodem půlkruhu a jeho poloha je na ose symetrie ve výšce h od základny (průměr půlkruhu):

h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm

Cvičení 4

Najděte moment setrvačnosti půlkruhu vzhledem k ose, která se shoduje s jeho průměrem, s vědomím, že půlkruh je vyroben z tenkého plechu. Jeho poloměr je 10 cm a jeho hmotnost je 100 gramů.

Řešení

Vzorec, který udává moment setrvačnosti půlkruhu, je:

Já_X = (π⋅R⁴) / 8

Ale protože nám problém říká, že se jedná o hmotný půlkruh, pak předchozí vztah musí být vynásoben povrchovou hustotou hmoty půlkruhu, která bude označena σ.

Já_X = σ (π⋅R⁴) / 8

Poté pokračujeme v určování σ, což není nic jiného než hmotnost půlkruhu dělená jeho oblastí.

Plocha byla určena v cvičení 2 a výsledek byl 157 cm^dva. Pak bude povrchová hustota tohoto půlkruhu:

σ = 100 gramů / 157 cm^dva = 0,637 g / cm^dva

Pak bude moment setrvačnosti vzhledem k průměru vypočítán takto:

Já_X = (0,637 g / cm^dva) [3,1416 ⋅ (10 cm)⁴] / 8

Výsledek:

Já_X = 2502 g⋅cm^dva

Cvičení 5

Určete moment setrvačnosti půlkruhu o poloměru 10 cm vyrobeného z materiálu s povrchovou hustotou 0,637 g / cm^dva podél osy, která prochází těžištěm a je rovnoběžná s jeho průměrem.

Řešení

K vyřešení tohoto cvičení je nutné si pamatovat Steinerovu větu o momentech setrvačnosti paralelních os, která říká:

Moment setrvačnosti I vzhledem k ose, která je ve vzdálenosti h od těžiště, se rovná součtu momentu setrvačnosti I_C vzhledem k ose, která prochází těžištěm a je rovnoběžná s první plus součin hmotnosti krát čtverce oddělení dvou os.

I = já_C + M h^dva

V našem případě je známo, který je moment setrvačnosti vzhledem k průměru, který byl již vypočítán v cvičení 4. Je také známa separace h mezi průměrem a těžištěm, která byla vypočítána v cvičení 3.

Musíme pouze vyčistit Ic:

Já_C = I - M h^dva

Já_C = 2502 g⋅cm^dva - 100 g ⋅ (4,246 cm)^dva výsledkem je, že moment setrvačnosti osou rovnoběžnou s průměrem a procházející těžištěm je: 

Já_C = 699,15 g⋅cm^dva

Reference

1. Alexander, D. 2013. Geometrie. 5. Edice. Cengage Learning.
2. Matematická otevřená reference. Půlkruh. Obnoveno z: mathopenref.com.
3. Půlkruh vesmíru vzorců. Obnoveno z: universoformulas.com.
4. Vesmírné vzorce. Plocha půlkruhu. Obnoveno z: universoformulas.com.
5. Wikipedia. Půlkruh. Obnoveno z: en.wikipedia.com.