
Příklady a cvičení výkonových řad
A výkonová řada se skládá ze součtu termínů ve formě mocnin proměnné X, nebo obecněji z x-c, kde C je konstantní reálné číslo. V součtové notaci je řada sil vyjádřena takto:
.An (x -c)n = anebo + na1 (x - c) + adva (x - c)dva + na3 (x - c)3 +… + An (x - c)n
Kde jsou koeficienty anebo, na1, nadva… Jsou reálná čísla a řada začíná na n = 0.

Tato série je zaměřena na hodnotu C který je konstantní, ale můžete si vybrat který C je rovno 0, v takovém případě se výkonová řada zjednodušuje na:
.An Xn = anebo + na1 x + adva Xdva + na3 X3 +… + An Xn
Série začíná nanebo(x-c)0 Y naneboX0 resp. Ale víme, že:
(x-c)0= x0 = 1
Proto nanebo(x-c)0 = naneboX0 = nanebo (nezávislý termín)
Dobrou věcí na výkonových řadách je, že s nimi můžete vyjadřovat funkce, což má mnoho výhod, zejména pokud chcete pracovat s komplikovanou funkcí.
V takovém případě se místo přímého použití funkce použije její rozšíření v napájecích řadách, které lze snáze odvodit, integrovat nebo pracovat numericky..
Samozřejmě je vše podmíněno konvergencí série. Řada konverguje, když přidáním určitého velkého počtu výrazů získáte pevnou hodnotu. A pokud ještě přidáme další výrazy, budeme nadále získávat tuto hodnotu.
Rejstřík článků
- 1 Funguje jako Power Series
- 1.1 Geometrická výkonová řada
- 2 Jak najít sériové rozšíření sil funkce
- 3 Cvičení
- 3.1 - Cvičení vyřešeno 1
- 3.2 - Cvičení vyřešeno 2
- 4 Odkazy
Funguje jako Power Series
Jako příklad funkce vyjádřené jako mocninová řada si vezměme f (x) = eX.
Tuto funkci lze vyjádřit pomocí řady pravomocí následovně:
aX ≈ 1 + x + (xdva / 2!) + (X3 / 3!) + (X4 / 4!) + (X5 / 5!) +…
Kde! = n. (n-1). (n-2). (n-3)… a trvá to 0! = 1.
Pomocí kalkulačky zkontrolujeme, zda se řada skutečně shoduje s funkcí výslovně danou. Začněme například tím, že x = 0.
Víme, že e0 = 1. Podívejme se, co série dělá:
a0 ≈ 1 + 0 + (0dva / 2!) + (03 / 3!) + (04 / 4!) + (05 / 5!) +… = 1
A teď to zkusme x = 1. Ukazuje to kalkulačka a1 = 2,71828, a pak pojďme porovnat s řadou:
a1 ≈ 1 + 1 + (1dva / 2!) + (13 / 3!) + (14 / 4!) + (15 / 5!) +… = 2 + 0,5000 + 0,1667 + 0,0417 + 0,0083 +… ≈ 2,7167
S pouhými 5 termíny již máme přesnou shodu e ≈ 2,71. Naší sérii zbývá ještě trochu víc, ale jak bude přidáno více termínů, řada jistě konverguje na přesnou hodnotu a. Znázornění je přesné kdy n → ∞.
Pokud se výše uvedená analýza opakuje do n = 2 jsou získány velmi podobné výsledky.
Tímto způsobem jsme si jisti, že exponenciální funkce f (x) = eX může být reprezentován touto řadou pravomocí:

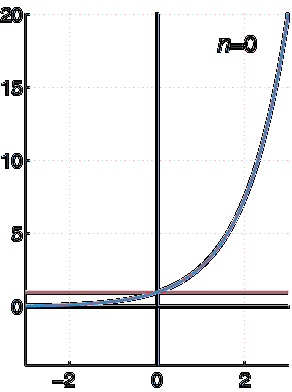
Geometrická řada sil
Funkce f (x) = eX není to jediná funkce, která podporuje reprezentaci mocninných řad. Například funkce F(x) = 1/1 - x vypadá hodně jako známý konvergentní geometrická řada:
.A.rn = a / 1 - r
Stačí udělat a = 1 a r = x, abychom získali řadu vhodnou pro tuto funkci, která je soustředěna na c = 0:

Je však známo, že tato řada je pro │r│ konvergentní<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.
Pokud chcete definovat tuto funkci v jiném intervalu, jednoduše se zaměřte na vhodnou hodnotu a jste hotovi..
Jak najít sériové rozšíření sil funkce
Jakoukoli funkci lze vyvinout v mocninové řadě se středem na c, pokud má derivace všech řádů na x = c. Postup využívá následující větu, tzv Taylorova věta:
Nechť f (x) je funkce s derivacemi řádu n, označeno jako F(n), který připouští sériové rozšiřování sil v intervalu Já. Jeho vývoj v Taylor série to je:

Aby:
f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)dva / 2 + f "(c) (x-c)3 / 6 +… Rn
Kde Rn, což je devátý člen řady, se nazývá zbytek:

Když c = 0, řada se volá Řada Maclaurin.
Tato řada zde uvedená je totožná se sérií uvedenou na začátku, pouze nyní máme způsob, jak explicitně najít koeficienty každého termínu dané:

Musí však být zajištěno, že řada konverguje k funkci, která má být reprezentována. Stává se, že ne každá Taylorova řada nutně konverguje k f (x), které mělo na mysli při výpočtu koeficientů nan.
To se děje proto, že možná deriváty funkce, hodnocené v x = c shodovat se stejnou hodnotou derivátů jiného, také v x = c. V tomto případě by byly koeficienty stejné, ale vývoj by byl nejednoznačný, protože není jisté, které funkci odpovídá..
Naštěstí existuje způsob, jak vědět:
Kritérium konvergence
Aby se zabránilo dvojznačnosti, pokud Rn → 0, když n → ∞ pro všechna x v intervalu I, řada konverguje k f (x).
Cvičení
- Vyřešené cvičení 1
Najděte pro danou funkci řadu geometrických výkonů f (x) = 1/2 - x se středem na c = 0.
Řešení
Daná funkce musí být vyjádřena tak, aby se co nejvíce shodovala s 1 / 1- x, jehož řada je známá. Přepíšeme tedy čitatele a jmenovatele, aniž bychom změnili původní výraz:
1/2 - x = (1/2) / [1 - (x / 2)]
Vzhledem k tomu, že ½ je konstantní, vychází ze součtu a je zapsáno z hlediska nové proměnné x / 2:

Všimněte si, že x = 2 nepatří do domény funkce a podle konvergenčního kritéria uvedeného v sekci Geometrická výkonová řada, rozšíření platí pro │x / 2│< 1 o equivalentemente -2 < x < 2.
- Cvičení vyřešeno 2
Najděte prvních 5 členů rozšíření řady Maclaurin funkce f (x) = sin x.
Řešení
Krok 1
Nejprve jsou nalezeny deriváty:
-Derivace řádu 0: je to stejná funkce f (x) = sin x
-První derivace: (sin x) '= cos x
-Druhá derivace: (sin x) "= (cos x) '= - sin x
-Třetí derivace: (sin x) "= (-sen x) '= - cos x
-Čtvrtý derivát: (sin x) "= (- cos x) '= sin x
Krok 2
Pak je každá derivace vyhodnocena při x = c, stejně jako Maclaurinova expanze, c = 0:
sin 0 = 0; cos 0 = 1; - sin 0 = 0; -cos 0 = -1; hřích 0 = 0
Krok 3
Jsou zkonstruovány koeficienty an;
nanebo = 0/0! = 0; na1 = 1/1! = 1; nadva = 0/2! = 0; na3 = -1 / 3!; na4 = 0/4! = 0
Krok 4
Nakonec je řada sestavena podle:

sin x ≈ 0,x0 + 1. x1 + 0 .xdva - (1/3!) X3 + 0,x4… = X - (1/3!)) X3 +...
Potřebuje čtenář více termínů? O kolik více se řada blíží funkci.
Všimněte si, že v koeficientech je vzor, další nenulový člen je a5 a všichni s lichým indexem se také liší od 0, střídají znaménka, takže:
sin x ≈ x - (1/3!)) x3 + (1/5!)) X5 - (1/7!)) X7 +... .
Ponechá se jako cvičení, aby se zkontrolovalo, že konverguje, můžete použít kritérium kvocientu pro konvergenci sérií.
Reference
- Nadace CK-12. Power Series: reprezentace funkcí a operací. Obnoveno z: ck12.org.
- Engler, A. 2019. Integrální počet. Národní univerzita v Litoralu.
- Larson, R. 2010. Výpočet proměnné. 9. Edice. Mcgraw kopec.
- Matematické texty zdarma. Silová řada. Obnoveno z: math.liibretexts.org.
- Wikipedia. Silová řada. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře