
Teorie charakteristických množin, prvků, příkladů, cvičení
The teorie množin Jedná se o obor logicko-matematiky, který je zodpovědný za studium vztahů mezi entitami zvanými množiny. Soupravy se vyznačují tím, že jde o sbírky předmětů stejné povahy. Tyto objekty jsou prvky sady a mohou to být: čísla, písmena, geometrické obrazce, slova, která představují objekty, samotné objekty a další.
Byl to Georg Cantor, který na konci 19. století navrhl teorii množin. Zatímco další významní matematici ve 20. století formovali: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel a další..

Vennovy diagramy představují grafický způsob reprezentace množiny a skládá se z uzavřené roviny, ve které jsou prvky množiny.
Například na obrázku 1 jsou znázorněny dvě sady A a B, které mají společné prvky, prvky společné pro A a B. Tyto tvoří novou sadu nazvanou průniková sada A a B, která je zapsána ve formě symbolické jako následuje:
A ∩ B
Rejstřík článků
- 1 Funkce
- 2 typy sad
- 2.1 Konečná množina
- 2.2 Nekonečná sada
- 2.3 Prázdná sada
- 2.4 Unitary set
- 2.5 Binární sada
- 2.6 Univerzální sada
- 3 Základní prvky
- 3.1 - Vztahy mezi sadami
- 3.2 - Vlastnosti zařazení
- 3.3 - Operace mezi sadami
- 4 příklady
- 4.1 Příklad 1
- 4.2 Příklad 2
- 4.3 Příklad 3
- 4.4 Příklad 4
- 4.5 Příklad 5
- 5 Cvičení vyřešena
- 5.1 Cvičení 1
- 5.2 Cvičení 2
- 5.3 Cvičení 3
- 5.4 Cvičení 4
- 6 Reference
Vlastnosti
Sada je primitivní koncept, protože v geometrii je to koncept bodu, přímky nebo roviny. Neexistuje lepší způsob vyjádření konceptu, než poukázáním na příklady:
Sada E tvořená barvami španělské vlajky. Tento způsob vyjádření množiny se nazývá porozumění. Stejná sada E napsaná příponou je:
E = červená, žlutá
V tomto případě jsou červená a žlutá prvky množiny E. Je třeba poznamenat, že prvky jsou uvedeny v závorkách a neopakují se. V případě španělské vlajky existují tři barevné pruhy (červený, žlutý, červený), z nichž dva se opakují, ale prvky se při vyjádření množiny neopakují..
Předpokládejme množinu V tvořenou prvními třemi písmeny samohlásek:
V = a, e, i
Síla výkonu V, označená jako P (V), je množina všech sad, které mohou být vytvořeny s prvky V:
P (V) = a, e, i, a, e, a, i, e, i, a, e, i
Druhy sad
Konečná sada
Jedná se o množinu, ve které lze spočítat její prvky. Příklady konečných množin jsou mimo jiné písmena španělské abecedy, španělské samohlásky, planety sluneční soustavy. Počet prvků konečné množiny se nazývá její mohutnost.
Nekonečná sada
Nekonečnou množinou se rozumí vše, co je počet jejích prvků nespočetný, protože bez ohledu na to, jak velký může být počet jejích prvků, je vždy možné najít více prvků.
Příkladem nekonečné množiny je množina přirozených čísel N, která je v extenzivní formě vyjádřena takto:
N = 1, 2, 3, 4, 5,…. Je zjevně nekonečná množina, protože bez ohledu na to, jak velké přirozené číslo může být, další největší lze vždy najít v nekonečném procesu. Je zřejmé, že mohutnost nekonečné množiny je ∞.
Prázdná sada
Je to sada, která neobsahuje žádný prvek. Prázdná množina V je označena Ø nebo dvojicí klíčů bez prvků uvnitř:
V = = Ø.
Prázdná množina je jedinečná, proto musí být nesprávné říkat „prázdná množina“, správný tvar je říkat „prázdná množina“.
Mezi vlastnostmi prázdné sady máme, že se jedná o podmnožinu jakékoli sady:
Ø ⊂ A
Kromě toho, pokud je množina podmnožinou prázdné množiny, pak nutně řečená množina bude vakuum:
A ⊂ Ø ⇔ A = Ø
Unitární sada
Sada jednotek je jakákoli sada, která obsahuje jeden prvek. Například sada přírodních satelitů Země je jednotná sada, jejíž jediným prvkem je Měsíc. Sada B celých čísel menších než 2 a větších než nula má pouze prvek 1, proto se jedná o jednotnou sadu.
Binární sada
Sada je binární, pokud má pouze dva prvky. Například množina X, takže x je řešení reálných čísel x ^ 2 = 2. Tato množina pomocí rozšíření je napsána takto:
X = -√2, + √2
Univerzální sada
Univerzální sada je sada, která obsahuje další sady stejného typu nebo povahy. Například univerzální množina přirozených čísel je množina reálných čísel. Skutečná čísla jsou ale univerzální množinou celých čísel a racionálních čísel.
Základní položky
- Vztahy mezi množinami
V sestavách lze mezi nimi a jejich prvky navázat různé typy vztahů. Pokud dvě sady A a B mají mezi sebou přesně stejné prvky, je vytvořen vztah rovnosti, označený takto:
NA = B
Pokud všechny prvky množiny A patří do množiny B, ale ne všechny prvky B patří do A, pak mezi těmito množinami existuje inkluzní vztah, který je označen takto:
A ⊂ B, ale B ⊄ A
Výše uvedený výraz zní: A je podmnožinou B, ale B není podmnožinou A.
K označení, že některé nebo některé prvky patří do sady, se používá symbol členství ∈, například se říká, že x prvek nebo prvky patří do sady A, se píše symbolicky takto:
x ∈ A
Pokud prvek nepatří do množiny A, je tento vztah zapsán takto:
a ∉ A
Vztah členství nastává mezi prvky množiny a množinou, s jedinou výjimkou sady síly, přičemž sada síly je kolekce nebo sada všech možných sad, které lze vytvořit s prvky uvedené sady.
Předpokládejme V = a, e, i, jeho výkonová sada je P (V) = a, e, i, a, e, a, i, e, i , a, e, i, v tomto případě se množina V stane prvkem množiny P (V) a lze ji zapsat:
V ∈ P (V)
- Vlastnosti začlenění
První vlastnost zahrnutí stanoví, že každá sada je obsažena sama o sobě, nebo jinými slovy, že se jedná o podmnožinu sebe sama:
A ⊂ A
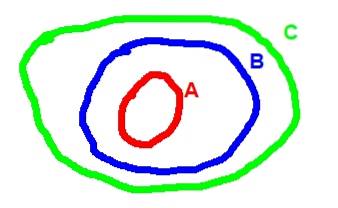
Druhou vlastností inkluze je tranzitivita: pokud A je podmnožinou B a B je zase podmnožinou C, pak A je podmnožinou C. V symbolické formě je relace tranzitivity psána takto:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C.
Níže je Vennův diagram odpovídající tranzitivitě inkluze:
- Operace mezi sadami
Průsečík
Průnik je operace mezi dvěma množinami, která vede k nové množině patřící do stejné univerzální množiny jako první dvě. V tomto smyslu se jedná o uzavřenou operaci.
Symbolicky je operace křižovatky formulována takto:
A⋂B = x / x∈A ^ x∈B
Příklad je následující: množina A písmen ve slově „elements“ a množina B písmen slova „opakovaně“, průnik mezi A a B se píše takto:
A⋂B = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s. Univerzální množina U A, B a také A⋂B je množina písmen španělské abecedy.
svaz
Spojení dvou sad je sada tvořená prvky společnými pro dvě sady a neobvyklými prvky dvou sad. Spojení mezi sadami je vyjádřeno symbolicky takto:
A∪B = x / x∈A v x∈B
Rozdíl
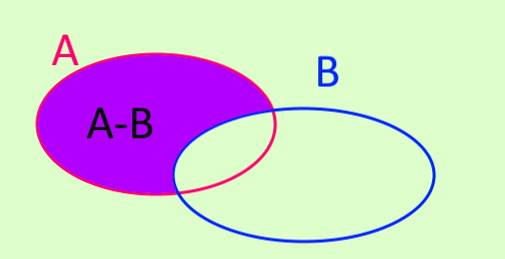
Diferenční operace množiny A mínus množina B je označena A-B. A-B je nová sada tvořená všemi prvky, které jsou v A a které nepatří do B. Symbolicky je to napsáno takto:
A - B = x / x ∈ A ^ x ∉ B
Symetrický rozdíl
Symetrický rozdíl je operace mezi dvěma sadami, kde výsledná sada je tvořena prvky, které nejsou společné pro dvě sady. Symetrický rozdíl je symbolicky znázorněn takto:
A⊕B = x / x∈ (A-B) ^ x∈ (B-A)
Příklady
Příklad 1
Vennův diagram je grafický způsob reprezentace množin. Například sada C písmen v sadě slov je znázorněna takto:

Příklad 2
Níže je znázorněno Vennovými diagramy, že množina samohlásek ve slově „množina“ je podmnožinou množiny písmen ve slově „množina“.

Příklad 3
Soubor Ñ písmen španělské abecedy je konečná množina, tato množinová přípona se píše takto:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z a jeho mohutnost je 27.
Příklad 4
Soubor PROTI samohlásek ve španělštině je podmnožinou množiny Ñ:
PROTI ⊂ Ñ proto je to konečná množina.
Konečná množina PROTI v rozsáhlé formě je to napsáno takto: PROTI = a, e, i, o, u a jeho mohutnost je 5.
Příklad 5
Vzhledem k množinám A = 2, 4, 6, 8 a B = 1, 2, 4, 7, 9 určete A-B a B-A.
A - B jsou prvky A, které nejsou v B:
A - B = 6, 8
B - A jsou prvky B, které nejsou v A:
B - A = 1, 7, 9
Vyřešená cvičení
Cvičení 1
Napište symbolickou formu a také rozšířením množiny P sudých přirozených čísel menších než 10.
Řešení: P = x∈ N / x < 10 ^ x mod 2 = 0
P = 2, 4, 6, 8
Cvičení 2
Předpokládejme množinu A, která je tvořena přirozenými čísly, která jsou faktory 210, a množinu B, která je tvořena prvočísly přirozených čísel menší než 9. Určete rozšířením obě množiny a určete, jaký vztah existuje mezi těmito dvěma množinami.
Řešení: Abychom určili prvky množiny A, musíme začít hledáním faktorů přirozeného čísla 210:
210 = 2 * 3 * 5 * 7
Pak se zapíše množina A:
A = 2, 3, 5, 7
Nyní uvažujeme množinu B, což je prvočísla menší než 9. 1 není prvočíslo, protože nesplňuje definici prvočísla: „číslo je prvočíslo právě tehdy, má-li přesně dva dělitele, 1 a samotné číslo“ . 2 je sudá a zároveň je prvočíslo, protože splňuje definici prvočísla, ostatní prvočísla menší než 9 jsou 3, 5 a 7. Takže množina B je:
B = 2, 3, 5, 7
Proto jsou obě sady stejné: A = B.
Cvičení 3
Určete množinu, jejíž prvky x se liší od x.
Řešení: C = x / x ≠ x
Vzhledem k tomu, že každý prvek, číslo nebo objekt se rovná sobě, nemůže být množina C jiná než prázdná množina:
C = Ø
Cvičení 4
Nechť množina N přirozených čísel a Z množina celých čísel. Určete N ⋂ Z a N ∪ Z.
Řešení:
N ⋂ Z = x ∈ Z / x ≤ 0 = (-∞, 0]
N ∪ Z = Z, protože N ⊂ Z.
Reference
- Garo, M. (2014). Matematika: kvadratické rovnice: Jak řešit kvadratickou rovnici. Marilù Garo.
- Haeussler, E.F., a Paul, R. S. (2003). Matematika pro management a ekonomiku. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matematika 1 SEP. Práh.
- Preciado, C. T. (2005). Kurz matematiky 3.. Redakční program.
- Mathematics 10 (2018). "Příklady konečných sad". Obnoveno z: matematicas10.net
- Wikipedia. Teorie množin. Obnoveno z: es.wikipedia.com

Zatím žádné komentáře