Varignonova věta

Co je Varignonova věta?

Varignonova věta v Mechanice uvádí, že součet momentů produkovaných soustavou souběžných sil vzhledem k určitému bodu se rovná okamžiku výsledné síly vzhledem ke stejnému bodu.

Z tohoto důvodu je tato věta známá také jako začátek okamžiků.

Ačkoli byl prvním, kdo vyslovil, byl to Holanďan Simon Stevin (1548-1620), tvůrce hydrostatického paradoxu, francouzský matematik Pierre Varignon (1654-1722), který mu dal konečnou podobu.

Příklad toho, jak Varignonova věta funguje v mechanice, je následující: Předpokládejme, že na bod působí jednoduchý systém dvou koplanárních a souběžných sil. F₁ Y F_dva, (označeno tučně kvůli jejich vektorovému znaku). Tyto síly způsobují vznik čisté nebo výsledné síly zvané F_R.

Každá síla vyvíjí točivý moment nebo moment kolem bodu O, který se vypočítá vektorovým součinem mezi polohovým vektorem r_OP a sílu F, kde r_OP je směrován z O do bodu souběžnosti P:

M_O1 = r_OP × F₁

M_O2 = r_OP × F_dva

Vzhledem k F_R = F₁ + F_dva, pak:

M_NEBO = r_OP × F₁ + r_OP × F_dva = M_O1 + M_O2

Ale jak r_OP je společným faktorem, tedy aplikace distribuční vlastnosti na křížový produkt:

M_NEBO = r_OP × (F₁ + F_dva) = r_OP × F_R                

Součet momentů nebo momentů každé síly vzhledem k bodu O je tedy ekvivalentní momentu výsledné síly vzhledem ke stejnému bodu.

Prohlášení a důkaz

Dovolit být systém N souběžných sil, tvořený F₁, F_dva, F₃... F_N, jehož linie působení se protínají v bodě P (viz obrázek 1), moment této silové soustavy M_NEBO, s ohledem na bod O je dán vztahem:

M_NEBO = r_OP × F₁ + r_OP × F_dva + r_OP × F₃ +... r_OP × F_N = r_OP × (F₁ + F_dva + F₃ +... F_N)

Demonstrace

K prokázání věty se využívá distribuční vlastnosti vektorového produktu mezi vektory.

Buďte silami F₁, F_dva, F₃... F_N aplikováno na body A₁, NA_dva, NA₃… TO_N a souběžně v bodě P. Výsledný moment tohoto systému, vzhledem k bodu O, nazvaný M_NEBO, je součet momentů každé síly vzhledem k uvedenému bodu:

M_NEBO = ∑ r_OAi × F_i

Kde součet jde od i = 1 do i = N, protože existuje N sil. Jelikož máme co do činění se souběžnými silami a protože vektorový produkt mezi paralelními vektory je nulový, stává se, že:

r_PAi × F_i = 0

S nulovým vektorem označeným jako 0.

Okamžik jedné ze sil vzhledem k O, například moment síly F_i aplikováno v A_i, píše se to takto:

M_{slyšel jsem} = r_OAi × F_i

Vektor polohy r_OAi  lze vyjádřit jako součet dvou polohových vektorů:

r_OAi = r_OP + r_PAi

Tímto způsobem moment o O síly F_i to je:

M_{slyšel jsem} = (r_OP + r_PAi) × F_i = (r_OP × F_i) + (r_PAi × F_i)

Ale poslední člen je nulový, jak bylo vysvětleno výše, protože r_PAi je v přímce akce F_i, Tím pádem:

M_{slyšel jsem} = r_OP × F_i

S vědomím, že moment systému vzhledem k bodu O je součtem všech jednotlivých momentů každé síly vzhledem k uvedenému bodu, pak:

M_NEBO = ∑ M_{slyšel jsem} = ∑ r_OP × F_i

Co r_OP je konstantní vychází ze součtu:

M_NEBO = r_OP × (∑ F_i)

Ale ∑ F_i je prostě čistá síla nebo výsledná síla F_R, je proto okamžitě učiněn závěr, že:

M_NEBO = r_OP × F_R

Příklad

Varignonova věta usnadňuje výpočet momentu síly F Pokud jde o bod O ve struktuře zobrazené na obrázku, je-li síla rozložena na její obdélníkové složky a vypočítá se moment každé z nich:

Aplikace Varignonovy věty

Když je známa výsledná síla systému, lze použít Varignonovu větu, která nahradí součet každého z momentů produkovaných silami, které ji tvoří, momentem výslednice.

Pokud systém sestává ze sil ve stejné rovině a bod, ke kterému se má vypočítat moment, patří do této roviny, je výsledný moment kolmý.

Například pokud jsou všechny síly v rovině xy, moment je směrován v ose z a zbývá jen najít jeho velikost a smysl, jako je tomu v příkladu popsaném výše.

V tomto případě nám Varignonova věta umožňuje spočítat výsledný moment systému součtem. Je to velmi užitečné v případě trojrozměrného silového systému, pro který a priori není znám směr výsledného momentu.

K řešení těchto cvičení je vhodné rozložit síly a polohové vektory na jejich obdélníkové složky a ze součtu momentů určit složky čistého momentu.

Cvičení vyřešeno

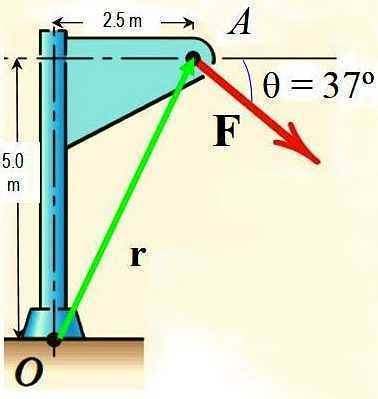
Pomocí Varignonovy věty vypočítáme moment síly F kolem bodu O zobrazeného na obrázku, pokud je velikost F 725 N.

Řešení

Chcete-li použít Varignonovu větu, rozložte sílu F ve dvou složkách, jejichž příslušné momenty kolem O jsou vypočítány a přidány k získání výsledného momentu.

F_X = 725 N ∙ cos 37 º = 579,0 N

F_Y = - 725 N N ∙ sin 37 º = −436,3 N

Podobně poziční vektor r směrovaný z O do A má komponenty:

r_X = 2,5 m

r_Y = 5,0 m

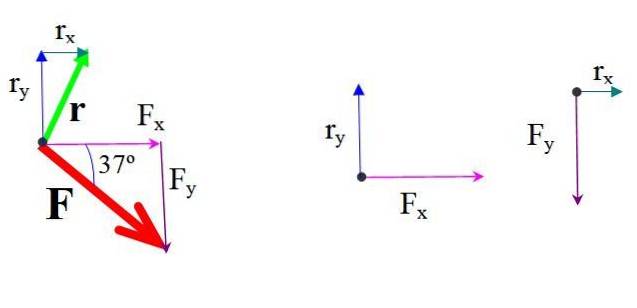
Okamžik každé složky síly kolem O se zjistí vynásobením síly a kolmé vzdálenosti.

Obě síly mají tendenci otáčet strukturu ve stejném směru, který je v tomto případě ve směru hodinových ručiček, kterému je libovolně přiřazeno kladné znaménko:

M_Vůl = F_X∙ r_Y ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m

M_Dobře = F_Y∙ r_X ∙ sin (−90 °) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m

Výsledný moment o O je:

M_NEBO = M_Vůl + M_Dobře = 3985,8 N ∙ m kolmo k rovině a ve směru hodinových ručiček.

Reference

1. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
2. Beer, F. 2010. Statické. McGraw Hill. 9. Edice.
3. Hibbeler, R. 1992. Mechanika pro inženýry. 6.. Edice. CECSA.
4. HK Engineering. Varignonova věta. Obnoveno z: youtube.com.
5. Wikipedia. Varignonova věta (mechanika). Obnoveno z: en.wikipedia.org.