
Základní věta o aritmetickém důkazu, aplikace, cvičení

The Základní teorém aritmetiky uvádí, že jakékoli přirozené číslo větší než 1 lze rozložit jako produkt prvočísel - některé lze opakovat - a tato forma je pro toto číslo jedinečná, i když pořadí faktorů může být odlišné.
Připomeňme si, že prvočíslo p Je to ten, kdo jako kladné dělitele připouští pouze sebe a 1. Následující čísla jsou prvočísla: 2, 3, 5, 7, 11, 13 atd., Protože existují nekonečna. Číslo 1 se nepovažuje za prvočíslo, protože má jediného dělitele.

Pokud jde o jejich část, jsou volána čísla, která neodpovídají výše uvedenému složená čísla, jako 4, 6, 8, 9, 10, 12, 14 ... Vezměme si například číslo 10 a okamžitě vidíme, že jej lze rozložit jako produkt 2 a 5:
10 = 2 × 5
Jak 2, tak 5 jsou ve skutečnosti prvočísla. Věta říká, že je to možné pro libovolné číslo n:
Kde str1, pdva, p3... strr jsou prvočísla ak1, kdva, k3,... kr jsou to přirozená čísla. Prvočísla tedy fungují jako cihly, ze kterých se násobením vytvářejí přirozená čísla.
Rejstřík článků
- 1 Důkaz základní věty o aritmetice
- 1.1 Jedinečnost primární faktorizace
- 2 Aplikace
- 2.1 Prvočísla v přírodě
- 2.2 Prvočísla a online nakupování
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Důkaz základní věty o aritmetice
Začneme tím, že ukážeme, že každé číslo lze rozložit na hlavní faktory. Dovolit být přirozené číslo n> 1, prvočíslo nebo složené.
Například pokud n = 2, lze jej vyjádřit jako: 2 = 1 × 2, což je prvočíslo. Stejným způsobem postupujte s následujícími čísly:
3 = 1 × 3
4 = 2 × 2
5 = 1 × 5
6 = 2 × 3
7 = 1 × 7
8 = 2 × 2 × 2
Pokračujeme takto a rozkládáme všechna přirozená čísla, dokud nedosáhneme čísla n -1. Uvidíme, jestli to dokážeme s následujícím číslem: n.
Pokud je n prvočíslo, můžeme jej rozložit jako n = 1 × n, ale předpokládejme, že n je složené a má dělitele d, logicky menší než n:
1< d < n.
Pokud n / d = p1, s P.1 prvočíslo, pak n se píše jako:
n = p1.d
Pokud je d prvočíslo, není už co dělat, ale pokud tomu tak není, existuje číslo ndva což je dělitel d a menší než toto: ndva < d, por lo que d podrá escribirse como el producto de ndva jiným prvočíslem strdva:
d = pdva ndva
To by při nahrazení původním číslem n dalo:
n = p1 .pdva .ndva
Nyní předpokládejme, že ndva buď je prvočíslo a my jej píšeme jako produkt prvočísla p3, tvým dělitelem n3, takový, že n3 < ndva < n1 < n:
ndva = str3.n3 → n = str1 pdva p3.n3
Tento postup opakujeme konečně, dokud nezískáme:
n = p1.pdva.p3 ... strr
To znamená, že je možné se rozložit každý celá čísla od 2 do n, jako produkt prvočísel.
Jedinečnost primární faktorizace
Nyní ověřme, že s výjimkou pořadí faktorů je tento rozklad jedinečný. Předpokládejme, že n lze zapsat dvěma způsoby:
n = p1.pdva.p3 ... strr = q1.codva.co3... cos (s r ≤ s)
Samozřejmě1, codva, co3... jsou také prvočísla. Jako p1 rozdělit (q1.codva.co3... cos) Pak p1 je rovno jakémukoli z „q“, na tom nezáleží ke kterému, takže můžeme říci, že p1 = q1. Vydělíme n p1 a dostaneme:
pdva.p3 ... strr =.codva.co3... cos
Postup opakujeme, dokud nedělíme vše pr, pak dostaneme:
1 = qr + 1... cos
K tomu se ale nelze dostatr + 1... cos = 1 když r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.
Aplikace
Jak jsme již řekli, prvočísla představují, pokud chcete, atomy čísel, jejich základní složky. Základní věta aritmetiky má tedy řadu aplikací, nejzřejmější: můžeme pracovat s velkými čísly snadněji, pokud je vyjádříme jako součin menších čísel..
Stejným způsobem můžeme najít největší společný násobek (LCM) a největšího společného dělitele (GCF), postup, který nám pomáhá snáze vytvářet součty zlomků, najít kořeny velkého počtu nebo pracovat s radikály, racionalizovat a řešit aplikační problémy velmi rozmanité povahy.
Prvočísla jsou navíc extrémně záhadná. Vzor v nich dosud nebyl rozpoznán a není možné vědět, který z nich bude další. Dosud největší byl nalezen počítači a má 24 862 048 číslice, i když se nová prvočísla objevují pokaždé méně často.
Prvočísla v přírodě
Cikády, cikádidos nebo cikády, které žijí na severovýchodě Spojených států, se objevují v cyklech 13 nebo 17 let. Obě jsou prvočísla.
Tímto způsobem se cikády vyhýbají shodě s predátory nebo konkurenty, kteří mají jiná období narození, ani různé odrůdy cikád navzájem nekonkurují, protože se neshodují během téhož roku..

Prvočísla a online nakupování
Prvočísla se v kryptografii používají k utajení údajů o kreditní kartě při nakupování přes internet. Tímto způsobem data, která kupující dorazí přesně do obchodu, aniž by se ztratila nebo padla do rukou bezohledných lidí..
Jak? Data na kartách jsou zakódována do čísla N, které lze vyjádřit jako součin prvočísel. Tato prvočísla jsou klíčem, který data odhalují, ale jsou veřejnosti neznámá, lze je dekódovat pouze na webu, na který jsou směrována.
Rozložit číslo na faktory je snadný úkol, pokud jsou čísla malá (viz řešená cvičení), ale v tomto případě se jako klíč používají prvočísla 100 číslic, která při jejich násobení dávají mnohem větší čísla, jejichž podrobný rozklad zahrnuje obrovský úkol.
Vyřešená cvičení
- Cvičení 1
Rozložte 1029 na hlavní faktory.
Řešení
1029 je dělitelné 3. Je známo, protože když přidáme jeho číslice, je součet násobkem 3: 1 + 0 + 2 + 9 = 12. Protože pořadí faktorů nemění součin, můžeme začít zde:
1029 3
343
1029 = 3 × 343
Na druhou stranu 343 = 73, pak:
1029 = 3 × 73 = 3 × 7 × 7 × 7
A protože 3 i 7 jsou prvočísla, jedná se o rozklad 1029.
- Cvičení 2
Faktor trinomiální xdva + 42x + 432.
Řešení
Trojčlen je přepsán ve tvaru (x + a). (x + b) a musíme najít hodnoty aab tak, že:
a + b = 42; a.b = 432
Číslo 432 se rozloží na primární faktory a odtud se zvolí vhodná kombinace metodou pokusu a omylu, takže přidané faktory dávají 42.
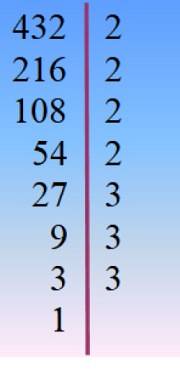
432 = 24 × 33 = 2 × 33× 23 = 24× 3dva × 3 =…
Odtud je několik možností, jak napsat 432:
432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .
A všechny lze najít kombinací produktů mezi hlavními faktory, ale k vyřešení navrhovaného cvičení je jedinou vhodnou kombinací: 432 = 24 × 18 od 24 + 18 = 42, pak:
Xdva + 42x + 432 = (x + 24). (x +18)
Reference
- Baldor, A. 1986. Teoretická praktická aritmetika. Compañía Cultural Editora de Textos Americanos S.A.
- BBC World. Skrytý zákoník přírody. Obnoveno z: bbc.com.
- De Leon, Manuel Prime čísla: strážci internetu. Obnoveno z: blogs.20minutos.es.
- UNAM. Teorie čísel I: Základní věta o aritmetice. Obnoveno z: teoriadenumeros.wikidot.com.
- Wikipedia. Základní věta o aritmetice. Obnoveno z: es.wikipedia.org.


Zatím žádné komentáře