
Charakteristické teselace, typy (pravidelné, nepravidelné), příklady
The mozaikový jsou povrchy pokryté jednou nebo více tzv dlaždice. Jsou všude: v ulicích a budovách všeho druhu. Tessera nebo dlaždice jsou ploché kusy, obvykle polygony se shodnými nebo izometrickými kopiemi, které jsou umístěny podle pravidelného vzoru. Tímto způsobem nezůstanou žádné mezery odkryté a dlaždice nebo mozaiky se nepřekrývají..
V případě, že je použit jeden typ mozaiky tvořený pravidelným mnohoúhelníkem, pak existuje a pravidelné mozaikování, ale pokud jsou použity dva nebo více typů pravidelných polygonů, pak je to a polopravidelná mozaikování.

A konečně, když polygony, které tvoří teselaci, nejsou pravidelné, pak je to a nepravidelná mozaikování.
Nejběžnějším typem mozaiky je mozaika tvořená obdélníkovými a zejména čtvercovými mozaikami. Na obrázku 1 máme dobrý příklad.
Rejstřík článků
- 1 Historie mozaikování
- 2 Pravidelné mozaikování
- 2.1 Názvosloví
- 2.2 Příklad 1: Trojúhelníková mozaikování
- 2.3 Příklad 2: Čtvercová mozaikování
- 2.4 Příklad 3: Hexagonální mozaikování
- 3 Polopravidelné mozaikování
- 3.1 Příklad 4: Tri-hexagonální mozaikování
- 3.2 Příklad 5: Tupá hexagonální mozaikování
- 3.3 Příklad 6: rhombi-tri-hexagonální mozaikování
- 4 Nepravidelné mozaikování
- 4.1 Příklad 7
- 4.2 Příklad 8
- 4.3 Příklad 9
- 4.4 Příklad 10: Káhirská mozaikování
- 4.5 Příklad 11: Teselace Al-Andalus
- 4.6 Příklad 12: mozaikování ve videohrách
- 5 Reference
Historie mozaikování
Po tisíce let se mozaikování používá k pokrytí podlah a stěn paláců a chrámů různých kultur a náboženství..
Například sumerská civilizace, která vzkvétala kolem roku 3500 před naším letopočtem. jižně od Mezopotámie, mezi řekami Eufrat a Tigris, použili ve své architektuře mozaikování.

Teselace také vzbudily zájem matematiků všech věkových skupin: počínaje Archimédem ve 3. století před naším letopočtem, následovaným Johannesem Keplerem v roce 1619, Camille Jordan v roce 1880, až po současnost Rogerem Penrosem..
Penrose vytvořil neperiodickou mozaikování známou jako Penroseova mozaikování. Atyto je jen několik jmen vědců, kteří hodně přispěli k mozaikování.
Pravidelné mozaikování
Pravidelné mozaikování se provádí pouze s jedním typem pravidelného mnohoúhelníku. Na druhou stranu, aby bylo mozaikování považováno za pravidelné, musí každý bod roviny:
-Patří do nitra mnohoúhelníku
-Nebo na okraj dvou sousedních polygonů
-Nakonec může patřit do společného vrcholu nejméně tří polygonů.
S výše uvedenými omezeními je možné ukázat, že pouze rovnostranné trojúhelníky, čtverce a šestiúhelníky mohou tvořit pravidelné mozaikování.
Nomenklatura
K dispozici je nomenklatura pro označení mozaikování, která se skládá ze seznamu ve směru hodinových ručiček a oddělených bodem, počtem stran polygonů, které obklopují každý uzel (nebo vrchol) mozaiky, vždy začínající polygonem s nejnižším číslem. strany.
Tato nomenklatura platí pro pravidelné a polopravidelné mozaikování.
Příklad 1: Trojúhelníková mozaikování
Obrázek 3 ukazuje pravidelnou trojúhelníkovou mozaikování. Je třeba poznamenat, že každý uzel trojúhelníkové mozaiky je společným vrcholem šesti rovnostranných trojúhelníků.
Způsob, jak označit tento typ teselace, je 3.3.3.3.3.3, který je také označen 36.

Příklad 2: Čtvercová mozaikování
Obrázek 4 ukazuje pravidelnou mozaikování složenou pouze ze čtverců. Je třeba poznamenat, že každý uzel v mozaikování je obklopen čtyřmi shodnými čtverci. Pro tento typ čtvercové mozaiky se použije notace: 4.4.4.4 nebo alternativně 44

Příklad 3: Šestihranná mozaikování
V hexagonální mozaikování je každý uzel obklopen třemi pravidelnými šestiúhelníky, jak je znázorněno na obrázku 5. Názvosloví pro pravidelnou hexagonální mozaikování je 6.6.6 nebo alternativně 63.

Polopravidelné mozaikování
Polopravidelné nebo archimédovské mozaiky se skládají ze dvou nebo více typů pravidelných polygonů. Každý uzel je obklopen typy polygonů, které tvoří teselaci, vždy ve stejném pořadí, a okrajová podmínka je zcela sdílena se sousedem..
Existuje osm polopravidelných mozaikování:
- 3.6.3.6 (trihexagonální mozaikování)
- 3.3.3.3.6 (tupá hexagonální mozaikování)
- 3.3.3.4.4 (prodloužená trojúhelníková mozaikování)
- 3.3.4.3.4 (tupá čtvercová mozaikování)
- 3.4.6.4 (rhombi-tri-hexagonální mozaikování)
- 4.8.8 (zkrácená čtvercová mozaikování)
- 3.12.12 (zkrácená hexagonální mozaikování)
- 4.6.12 (zkrácená trihexagonální mozaikování)
Některé příklady polopravidelných mozaikování jsou uvedeny níže.
Příklad 4: Tri-hexagonální mozaikování
Je to ten, který je složen z rovnostranných trojúhelníků a pravidelných šestiúhelníků ve struktuře 3.6.3.6, což znamená, že uzel mozaikování je obklopen (až do dokončení jednoho kola) trojúhelníkem, šestiúhelníkem, trojúhelníkem a šestiúhelníkem. Obrázek 6 ukazuje takovou mozaikování.

Příklad 5: Tupá hexagonální mozaikování
Stejně jako teselace v předchozím příkladu se i tento skládá z trojúhelníků a šestiúhelníků, ale jejich distribuce kolem uzlu je 3.3.3.3.6. Obrázek 7 jasně ilustruje tento typ mozaikování.

Příklad 6: rhombi-tri-hexagonální mozaikování
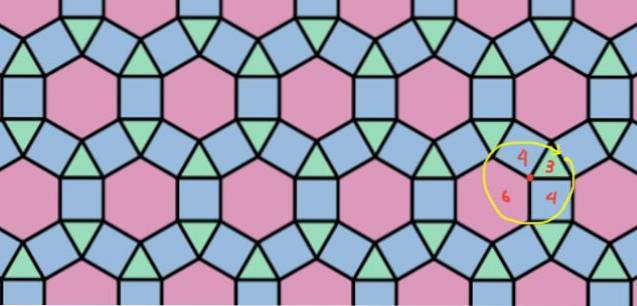
Jedná se o mozaikování, které se skládá z trojúhelníků, čtverců a šestiúhelníků v konfiguraci 3.4.6.4, která je znázorněna na obrázku 8.
Nepravidelné mozaikování
Nepravidelné mozaiky jsou ty, které jsou tvořeny nepravidelnými polygony nebo pravidelnými polygony, ale nesplňují kritérium, že uzel je vrcholem alespoň tří polygonů.
Příklad 7
Obrázek 9 ukazuje příklad nepravidelné mozaikování, ve kterém jsou všechny polygony pravidelné a shodné. Je nepravidelný, protože uzel není běžným vrcholem alespoň tří čtverců a existují také sousední čtverce, které úplně nesdílejí hranu.
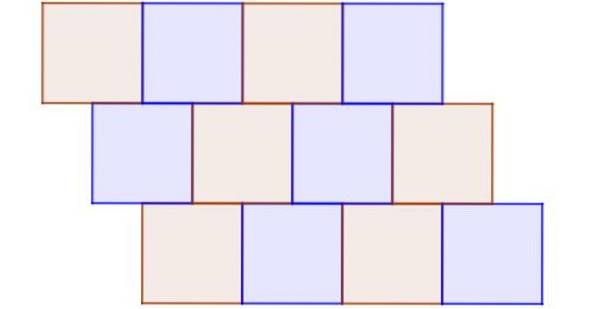
Příklad 8
Rovnoběžník vykládá plochý povrch, ale pokud to není čtverec, nemůže vytvořit pravidelnou mozaikování.

Příklad 9
Nepravidelné šestiúhelníky se střední symetrií tessellate plochý povrch, jak je znázorněno na následujícím obrázku:

Příklad 10: Káhirská mozaikování
Jedná se o velmi zajímavou mozaikování složenou z pětiúhelníků se stranami stejné délky, ale s nerovnými úhly, z nichž dva jsou rovné a ostatní tři mají každý 120 °..
Jeho název vychází ze skutečnosti, že toto mozaikování se nachází na chodníku některých ulic egyptské Káhiry. Obrázek 12 ukazuje mozaikování Káhiry.

Příklad 11: Teselace Al-Andalus
Teselace v některých částech Andalusie a severní Afriky se kromě okrasných prvků, jako je vegetace, vyznačuje také geometrií a epigrafií..
Teselace paláců, jako je palác Alhambra, byla tvořena dlaždicemi vyrobenými z keramických kousků mnoha barev, s několika (ne-li nekonečnými) tvary, které rozpoutaly geometrické vzory..

Příklad 12: mozaikování ve videohrách
Také známý jako tesellation, je to jedna z nejpopulárnějších novinek ve videohrách. Jde o vytváření textur pro simulaci mozaikování různých scénářů, které se v simulátoru objevují.
To je jasný odraz toho, že se tyto povlaky nadále vyvíjejí a překračují hranice reality..
Reference
- Užijte si matematiku. Mozaikování. Obnoveno z: gustolasmatematicas.com
- Rubiños. Tessellations vyřešil příklady. Obnoveno z: matematicasn.blogspot.com
- Weisstein, Eric W. „Demiregular tessellation“. Weisstein, Eric W, ed. MathWorld. Wolfram Research.
- Wikipedia. Mozaikování. Obnoveno z: es.wikipedia.com
- Wikipedia. Pravidelná mozaikování. Obnoveno z: es.wikipedia.com


Zatím žádné komentáře