Existuje přenos tepla když energie jde z jednoho těla do druhého kvůli rozdílu teplot mezi nimi. Proces přenosu tepla přestane, jakmile se teploty kontaktovaných těles vyrovnají nebo když je kontakt mezi nimi vyloučen..
Říká se množství energie přenesené z jednoho těla do druhého v daném časovém období přenesené teplo. Jedno tělo může dát teplo druhému nebo ho může absorbovat, ale teplo vždy jde z těla s nejvyšší teplotou do těla s nejnižší teplotou..
Jednotky tepla jsou stejné jako jednotky energie a v mezinárodním systému měření (SI) je joule (J). Dalšími často používanými jednotkami tepla jsou kalorie a BTU..
Pokud jde o matematické zákony, které řídí přenos tepla, závisí na mechanismu, který je součástí výměny..
Když je teplo vedeno z jednoho tělesa do druhého, je rychlost výměny tepla úměrná teplotnímu rozdílu. Toto je známé jako Fourierův zákon tepelné vodivosti, což vede k Newtonův zákon chlazení.
Rejstřík článků
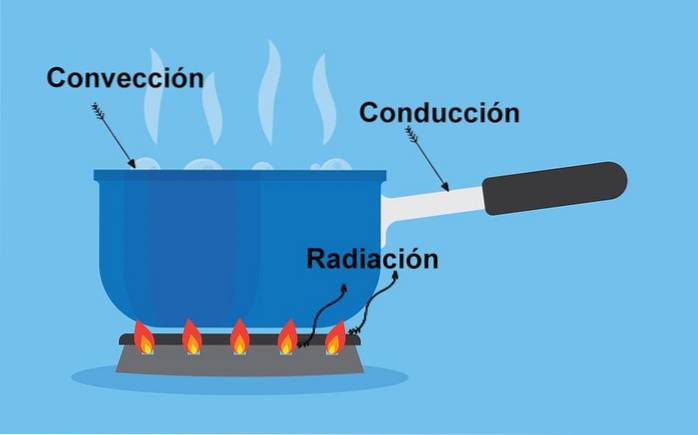
Jsou to způsoby, kterými lze vyměňovat teplo mezi dvěma těly. Rozeznávají se tři mechanismy:
-Řízení
-Proudění
-Záření
V hrnci, jako je ten, který je zobrazen na obrázku výše, existují tyto tři mechanismy přenosu tepla:
-Kov v hrnci se ohřívá především vedením.
-Voda a vzduch se konvekcí zahřívají a stoupají.
-Vyzařované záření ohřívá lidi poblíž hrnce.
Vedení tepla se vyskytuje většinou v pevných látkách, zejména v kovech.
Například sporák v kuchyni přenáší teplo na jídlo uvnitř hrnce prostřednictvím vodivého mechanismu přes kov dna a kovové stěny nádoby. V tepelném vedení nedochází k transportu materiálu, pouze k energii.
Konvekční mechanismus je typický pro kapaliny a plyny. Ty jsou při vyšších teplotách téměř vždy méně husté, z tohoto důvodu dochází k přenosu tepla z teplejších částí tekutiny do vyšších oblastí s chladnějšími částmi tekutiny. V konvekčním mechanismu je transport materiálu.
Radiační mechanismus umožňuje výměnu tepla mezi dvěma tělesy, i když nejsou v kontaktu. Okamžitým příkladem je Slunce, které ohřívá Zemi v prázdném prostoru mezi nimi..
Všechna těla emitují a absorbují elektromagnetické záření. Pokud máte dvě těla o různých teplotách, i když jsou ve vakuu, po chvíli dosáhnou stejné teploty díky výměně tepla elektromagnetickým zářením.
V termodynamických systémech v rovnováze záleží na množství celkového tepla vyměněného s prostředím, takže systém přechází z jednoho stavu rovnováhy do druhého.
Na druhé straně se v přenosu tepla zájem zaměřuje na přechodný jev, kdy systémy ještě nedosáhly tepelné rovnováhy. Je důležité si uvědomit, že množství tepla se vyměňuje v určitém časovém období, to znamená, že existuje rychlost přenosu tepla.
Při tepelné vodivosti se tepelná energie přenáší prostřednictvím srážek mezi atomy a molekulami materiálu, ať už je to pevná látka, kapalina nebo plyn..
Pevné látky jsou lepšími vodiči tepla než plyny a kapaliny. V kovech jsou volné elektrony, které se mohou pohybovat kovem.
Protože volné elektrony mají velkou mobilitu, jsou schopny efektivněji přenášet kinetickou energii srážkami, proto mají kovy vysokou tepelnou vodivost..
Z makroskopického hlediska se tepelná vodivost měří jako množství tepla přeneseného za jednotku času nebo kalorický proud H:
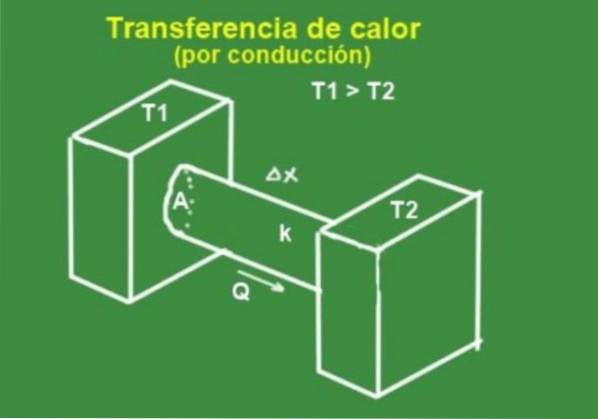
Kalorický proud H je úměrná průřezu plochy NA a teplotní změny na jednotku podélné vzdálenosti.
Tato rovnice se použije k výpočtu kalorického proudu H tyče, jako je ta na obrázku 2, která je mezi dvěma teplotními zásobníky T1 Y Tdva respektive bytí T1> Tdva.
Níže je uveden seznam tepelné vodivosti některých materiálů ve wattech na metr na kelvin: W / (m. K)
Hliník -205
Měď -385
Stříbro - 400
Ocel -50
Korek nebo sklolaminát - 0,04
Beton nebo sklo -0,8
Dřevo - 0,05 až 0,015
Vzduch - 0,024
Při konvekci tepla se energie přenáší v důsledku pohybu tekutiny, která má při různých teplotách různé hustoty. Když se například vaří voda v hrnci, zvyšuje se teplota vody u dna, takže se rozpíná.
Díky této expanzi stoupá horká voda, zatímco studená klesá dolů a zabírá prostor, který zanechala horká voda, která stoupala. Výsledkem je cirkulační pohyb, který pokračuje, dokud se teploty všech úrovní nevyrovnají..
Konvekce určuje to, co určuje pohyb velkých vzdušných hmot v zemské atmosféře, a také určuje cirkulaci mořských proudů..
V mechanismech přenosu tepla vedením a konvekcí je pro přenos tepla vyžadována přítomnost materiálu. Na druhé straně v radiačním mechanismu může teplo procházet z jednoho těla do druhého vakuem..
Jedná se o mechanismus, kterým slunce při vyšší teplotě než Země přenáší energii na naši planetu přímo vakuem vesmíru. Radiace se k nám dostává elektromagnetickými vlnami.
Všechny materiály jsou schopné emitovat a absorbovat elektromagnetické záření. Maximum emitované nebo absorbované frekvence závisí na teplotě materiálu a tato frekvence se zvyšuje s teplotou..
Převládající vlnová délka v emisním nebo absorpčním spektru černého tělesa sleduje Vídeňské právo, který říká, že převládající vlnová délka je úměrná inverzní hodnotě tělesné teploty.
Na druhou stranu výkon (ve wattech), kterým tělo emituje nebo absorbuje tepelnou energii elektromagnetickým zářením, je úměrný čtvrtému výkonu absolutní teploty. Toto je známé jako Stefanův zákon:
P = εAσT4
Ve výše uvedeném výrazu σ je Stefanova konstanta a její hodnota je 5,67 x 10-8 W / mdva K.4. NA je povrch těla a ε je emisivita materiálu, bezrozměrná konstanta, jejíž hodnota je mezi 0 a 1, a závisí na materiálu.
Zvažte lištu na obrázku 2. Předpokládejme, že lišta je 5 cm dlouhá, poloměr 1 cm a je vyrobena z mědi..
Lišta je umístěna mezi dvě stěny, které udržují její konstantní teplotu. První stěna má teplotu T1 = 100 ° C, zatímco druhá má teplotu T2 = 20 ° C. Určit:
a.- Hodnota tepelného proudu H
b. - Teplota měděného prutu při 2 cm, 3 cm a 4 cm od teplotní stěny T1.
Protože měděná tyč je umístěna mezi dvěma stěnami, jejichž stěny udržují po celou dobu stejnou teplotu, lze říci, že je v ustáleném stavu. To znamená, že tepelný proud H má pro každý okamžik stejnou hodnotu.
Pro výpočet tohoto proudu použijeme vzorec, který spojuje proud H s rozdílem teplot a délkou sloupce.
Průřez je:
A = πRdva = 3,14 * (1 × 10-dvam)dva = 3,14 x 10-4 mdva
Teplotní rozdíl mezi konci tyče je
ΔT = (100 ° C - 20 ° C) = (373K - 293K) = 80K
Δx = 5 cm = 5 x 10-dva m
V = 385 W / (m K) * 3,14 x 10-4 mdva * (80 tis. / 5 x 10-dva m) = 193,4 W.
Tento proud je stejný v každém bodě lišty a v každém okamžiku, protože bylo dosaženo ustáleného stavu..
V této části jsme požádáni o výpočet teploty Tp v určitém okamžiku P nachází se na dálku Xp vzhledem ke zdi T1.
Výraz, který dává kalorický proud H na místě P to je:
H = k A (T1 -Tp) / (Xp)
Z tohoto výrazu to lze vypočítat Tp přes:
Tp = T1 - (H Xp) / (k A) = 373 K - (193,4 W / (385 W / (m K) 3,14 x 10)-4 mdva)) * Xp
Tp = 373 K - 1620,4 (K / m) * Xp
Pojďme vypočítat teplotu Tp v pozicích 2 cm, 3 cm a 4 cm, nahrazením číselných hodnot:
Zatím žádné komentáře