
Vlastnosti lichoběžníkového scalenu, vzorce a rovnice, příklady
A trapéz scalene je mnohoúhelník se čtyřmi stranami, z nichž dvě jsou navzájem rovnoběžné a se čtyřmi vnitřními úhly různých měr.
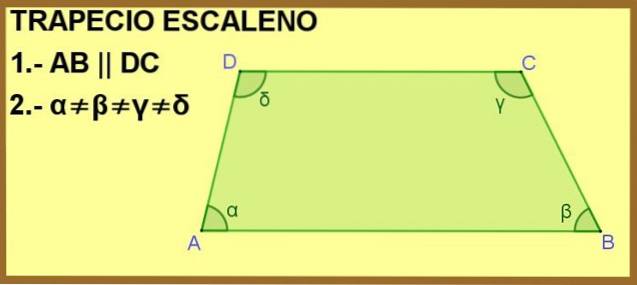
Čtyřúhelník ABCD je zobrazen níže, kde strany AB a DC jsou navzájem rovnoběžné. To je dost na to, aby se z něj stal lichoběžník, ale navíc jsou vnitřní úhly α, β, γ a δ různé, proto je lichoběžník scalen.
Rejstřík článků
- 1 Prvky scalenového lichoběžníku
- 1.1 Ostatní lichoběžníky
- 2 Vlastnosti
- 3 Vzorce a rovnice
- 3.1 Výška
- 3,2 Medián
- 3.3 Úhlopříčky
- 3,4 Obvod
- 3.5 Plocha
- 3.6 Další vztahy pro lichoběžník scalene
- 4 Konstrukce scalenového lichoběžníku s pravítkem a kompasem
- 5 Příklad
- 5.1 - Řešení a
- 5.2 - Řešení b
- 6 Cvičení vyřešeno
- 6.1 Řešení
- 7 Reference
Prvky scalenového lichoběžníku
Zde jsou nejcharakterističtější prvky:
-Základny a boky: rovnoběžné strany lichoběžníku jsou jeho základny a dvě nerovnoběžné strany jsou boční.
Ve scalenovém lichoběžníku jsou základny různé délky a také boční. Scalenový lichoběžník však může mít boční délku rovnou délce k základně..
-Medián: je segment, který spojuje středy bočnic.
-Úhlopříčky: úhlopříčka lichoběžníku je segment, který spojuje dva protilehlé vrcholy. Lichoběžník, stejně jako každý čtyřúhelník, má dvě úhlopříčky. Ve scalenovém lichoběžníku mají různou délku.
Ostatní lichoběžníky
Kromě lichoběžníkového scalenu existují další zvláštní lichoběžníky: pravý lichoběžník a rovnoramenný lichoběžník..
Lichoběžník je obdélník, když jeden z jeho úhlů má pravdu, zatímco rovnoramenný lichoběžník má strany stejné délky.
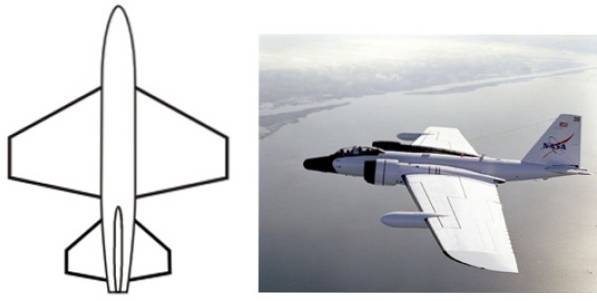
Lichoběžníkový tvar má řadu aplikací na konstrukční a průmyslové úrovni, například v konfiguraci křídel letadel, ve tvaru předmětů každodenní potřeby, jako jsou stoly, opěradla židlí, obaly, peněženky, potisky textilu a další..
Vlastnosti
Níže jsou uvedeny vlastnosti lichoběžníkového scalenu, z nichž mnohé sahají až k dalším typům lichoběžníku. V následujícím textu, když mluvíme o „lichoběžníku“, bude vlastnost použitelná pro jakýkoli typ, včetně scalenu..
1. Medián lichoběžníku, tj. Segmentu, který spojuje středy jeho nerovnoběžných stran, je rovnoběžný s jakoukoli základnou.
2. - Medián lichoběžníku má délku, která je polovičním součtem jeho základen a prořízne jeho úhlopříčky ve středu.
3.- Úhlopříčky lichoběžníku se protínají v bodě, který je rozděluje na dvě části, které jsou úměrné kvocientům bází.
4.- Součet čtverců úhlopříček lichoběžníku se rovná součtu čtverců jeho stran plus dvojnásobný součin jeho základen..
5. - Segment, který spojuje střední body úhlopříček, má délku rovnou semifinále základen.
6.- Úhly sousedící s bočními úhly jsou doplňkové.
7. - U lichoběžníku scalene je délka jeho úhlopříček odlišná.
8. - Lichoběžník má zapsaný obvod pouze v případě, že součet jeho základen se rovná součtu jeho stran.
9. - Pokud má lichoběžník vepsaný obvod, pak úhel s vrcholem ve středu uvedeného obvodu a po stranách, které procházejí konci strany lichoběžníku, je rovný.
10. - Scalenový lichoběžník nemá ohraničený obvod, jediný typ lichoběžníku, který ho má, jsou rovnoramenné.
Vzorce a rovnice
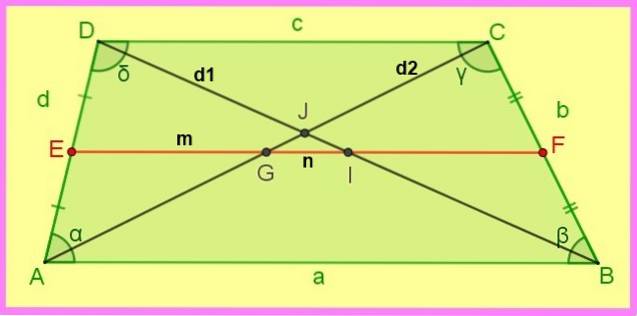
Následující vztahy scalenového lichoběžníku jsou uvedeny na následujícím obrázku.
1. - Pokud AE = ED a BF = FC → EF || AB a EF || DC.
2. - EF = (AB + DC) / 2, tj .: m = (a + c) / 2.
3. - DI = IB = d1 / 2 a AG = GC = ddva /dva.
4. - DJ / JB = (c / a) podobně CJ / JA = (c / a).
5. - DBdva + ACdva = ADdva + před naším letopočtemdva + 2 AB ∙ DC
Ekvivalentně:
d1dva + ddvadva = ddva + bdva + 2 a ∙ c
6. - GI = (AB - DC) / 2
A to:
n = (a - c) / 2
7. - α + δ = 180⁰ a β + γ = 180⁰
8. - Pokud α ≠ β ≠ γ ≠ δ pak d1 ≠ d2.
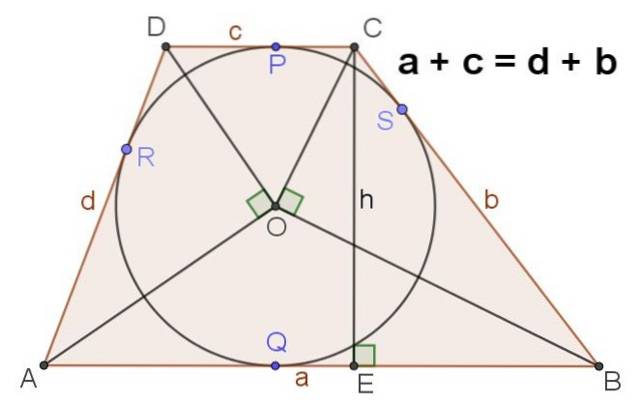
9. - Obrázek 4 ukazuje scalenový lichoběžník, který má vepsaný obvod, v tomto případě platí, že:
a + c = d + b
10. - Ve scalenovém lichoběžníku ABCD s vepsaným obvodem středu O platí také toto:
∡AOD = ∡BOC = 90⁰
Výška
Výška lichoběžníku je definována jako segment, který vede z bodu základny kolmo k opačné základně (nebo k jejímu prodloužení).
Všechny výšky lichoběžníku mají stejné měření h, takže většinu času slovo výška odkazuje na jeho měření. Při syntéze je výška vzdálenost nebo vzdálenost mezi bázemi.
Výška h může být určena znalostem délky jedné strany a jednoho z úhlů sousedících se stranou:
h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)
Medián
Míra mediánu lichoběžníku je poločetem bází:
m = (a + b) / 2
Úhlopříčky
d1 = √ [adva + ddva - 2 ∙ a ∙ d ∙ Cos (α)]
ddva= √ [adva + bdva - 2 ∙ a ∙ b ∙ Cos (β)]
Lze jej také vypočítat, pokud je známa pouze délka stran lichoběžníku:
d1 = √ [bdva + a ∙ c - a (nardva - ddva) / (a - c)]
ddva = √ [ddva + a ∙ c - a (ddva - bdva) / (a - c)]
Obvod
Obvod je celková délka obrysu, tj. Součet všech jeho stran:
P = a + b + c + d
Plocha
Plocha lichoběžníku je poločetem jeho základen vynásobeným jeho výškou:
A = h ∙ (a + b) / 2
Lze jej také vypočítat, pokud jsou známy střední hodnoty ma výška h:
A = m ∙ h
V případě, že je známa pouze délka stran lichoběžníku, lze plochu určit pomocí Heronova vzorce pro lichoběžník:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Kde s je semiperimetr: s = (a + b + c + d) / 2.
Další vztahy pro lichoběžník scalene
Průsečík mediánu s úhlopříčkami a rovnoběžka, která prochází průsečíkem úhlopříček, vede k dalším vztahům.
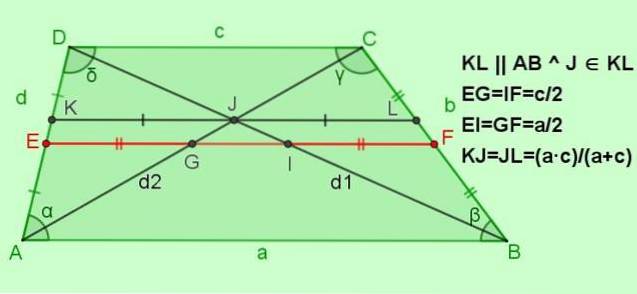
-Vztahy pro střední EF
EF = (a + c) / 2; EG = IF = c / 2; EI = GF = a / 2
-Vztahy pro segment rovnoběžný se základnami KL a procházející bodem J průsečík úhlopříček
Pokud KL || AB || DC s J ∈ KL, pak KJ = JL = (a ∙ c) / (a + c)
Konstrukce scalenového lichoběžníku s pravítkem a kompasem
Vzhledem k základnám délek na Y C, kde a> c a se stranami délek b a d, bytost b> d, postupujte podle těchto kroků (viz obrázek 6):
1. - S pravidlem je nakreslen segment hlavní AB.
2. - Od A se a na AB je bod P označen tak, že AP = c.
3. - S kompasem se středem v P a poloměrem d je nakreslen oblouk.
4. - Vycentrujte na B s poloměrem b a nakreslete oblouk, který zachytí oblouk nakreslený v předchozím kroku. Říkáme Q průsečík.
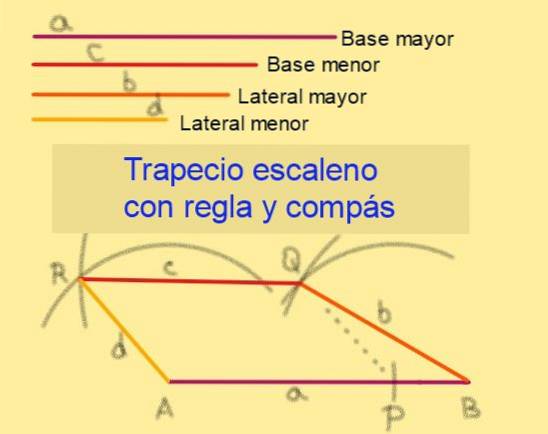
5. - Se středem v A nakreslete oblouk o poloměru d.
6. - Se středem v Q nakreslete oblouk o poloměru c, který zachytí oblouk nakreslený v předchozím kroku. Mezní bod se bude jmenovat R.
7. - Segmenty BQ, QR a RA jsou sledovány pomocí pravítka.
8. - Čtyřúhelník ABQR je scalenový lichoběžník, protože APQR je rovnoběžník, který zaručuje, že AB || Qr.
Příklad
Následující délky jsou uvedeny v cm: 7, 3, 4 a 6.
a) Určete, zda s nimi je možné zkonstruovat scalenový lichoběžník, který může ohraničovat kruh.
b) Najděte obvod, plochu, délku úhlopříček a výšku lichoběžníku, stejně jako poloměr vepsané kružnice.
- Řešení
Pomocí segmentů délky 7 a 3 jako základen a segmentů délky 4 a 6 jako bočnic lze sestrojit scalenový lichoběžník pomocí postupu popsaného v předchozí části.
Zbývá zkontrolovat, zda má vepsaný obvod, ale pamatuji si vlastnost (9):
Lichoběžník má zapsaný obvod pouze v případě, že součet jeho základen se rovná součtu jeho stran.
Vidíme to efektivně:
7 + 3 = 4 + 6 = 10
Poté je splněna podmínka existence zapsaného obvodu.
- Řešení b
Obvod
Obvod P se získá přidáním stran. Vzhledem k tomu, že základny přidávají až 10 a bočnice také, obvod je:
P = 20 cm
Plocha
Pro určení oblasti známé pouze její strany se použije vztah:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Kde s je semiperimetr:
s = (a + b + c + d) / 2.
V našem případě má semiperimetr hodnotu s = 10 cm. Po nahrazení příslušných hodnot:
a = 7 cm; b = 6 cm; c = 3 cm; d = 4 cm
Zůstává:
A = [10/4] √ [(3) (7) (- 1) (- 3)] = (5/2) √63 = 19,84 cm².
Výška
Výška h souvisí s oblastí A následujícím výrazem:
A = (a + c) ∙ h / 2, ze kterého lze zjistit výšku vymazáním:
h = 2A / (a + c) = 2 * 19,84 / 10 = 3,988 cm.
Poloměr vepsané kružnice
Poloměr vepsané kružnice se rovná polovině výšky:
r = h / 2 = 1984 cm
Úhlopříčky
Nakonec se zjistí délka úhlopříček:
d1 = √ [bdva + a ∙ c - a (nardva - ddva) / (a - c)]
ddva = √ [ddva + a ∙ c - a (ddva - bdva) / (a - c)]
Při správném nahrazení hodnot máme:
d1 = √ [6dva + 7 ∙ 3 - 7 (6dva - 4dva) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)
ddva = √ [4dva + 7 ∙ 3 - 7 (4dva - 6dva) / (7 - 3)] = √ (16 + 21-7 (-20) / 4) = √ (72)
To je: d1 = 4,69 cm a ddva = 8,49 cm
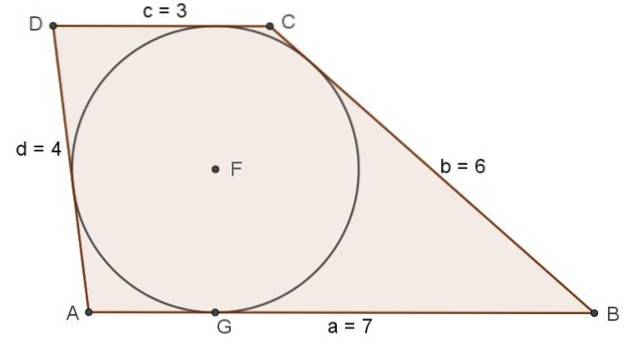
Cvičení vyřešeno
Určete vnitřní úhly lichoběžníku se základnami AB = a = 7, CD = c = 3 a bočními úhly BC = b = 6, DA = d = 4.
Řešení
Kosinovou větu lze použít k určení úhlů. Například úhel ∠A = α je určen z trojúhelníku ABD s AB = a = 7, BD = d2 = 8,49 a DA = d = 4.
Kosinová věta aplikovaná na tento trojúhelník vypadá takto:
ddvadva = adva + ddva - 2 ∙ a ∙ d ∙ Cos (α), to znamená:
72 = 49 + 16-56 ∙ Cos (α).
Řešení pro, kosinus úhlu α se získá:
Cos (α) = -1/8
To znamená, že α = ArcCos (-1/8) = 97,18⁰.
Stejným způsobem se získají ostatní úhly, jejichž hodnoty jsou:
p = 41,41⁰; γ = 138,59⁰ a nakonec δ = 82,82⁰.
Reference
- C. E. A. (2003). Prvky geometrie: s cvičeními a geometrií kompasu. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematika 2. Grupo Redakční Patria.
- Freed, K. (2007). Objevte mnohoúhelníky. Benchmark Education Company.
- Hendrik, V. (2013). Zobecněné polygony. Birkhäuser.
- IGER. (s.f.). Matematika v prvním semestru Tacaná. IGER.
- Jr. geometrie. (2014). Mnohoúhelníky. Lulu Press, Inc..
- Miller, Heeren a Hornsby. (2006). Mathematics: Reasoning And Applications (desáté vydání). Pearson Education.
- Patiño, M. (2006). Matematika 5. Redakční program.
- Wikipedia. Trapéz. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře