
Oválné (geometrické obrazce) charakteristiky, příklady, cvičení
The ovál symetrická je definována jako plochá a uzavřená křivka, která má dvě kolmé osy symetrie - jednu hlavní a jednu menší - a je tvořena dvěma obvodovými oblouky rovnými dvěma dvěma.
Tímto způsobem jej lze nakreslit pomocí kompasu a některých referenčních bodů na jedné z linií symetrie. V každém případě existuje několik způsobů, jak to nakreslit, jak uvidíme později.

Je to velmi známá křivka, protože je rozpoznána jako obrys elipsy, což je zvláštní případ oválu. Ovál však není elipsa, i když někdy vypadá velmi podobně, protože jeho vlastnosti a rozložení se liší. Například elipsa není konstruována pomocí kompasu.
Rejstřík článků
- 1 Funkce
- 2 Příklady
- 2.1 Konstrukce oválu pomocí soustředných kruhů
- 3 cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Vlastnosti
Ovál má velmi rozmanité aplikace: architektura, průmysl, grafický design, hodinářství a šperky jsou jen některé oblasti, kde vyniká jeho použití..
Nejvýraznější charakteristiky této důležité křivky jsou následující:
-Patří do skupiny technických křivek: kreslí se vytvářením obvodových oblouků pomocí kompasu.
-Všechny jeho body jsou ve stejné rovině.
-Chybí křivky nebo smyčky.
-Jeho uspořádání je spojité.
-Křivka oválu by měla být hladká a konvexní.
-Když kreslíte přímku tečnou k oválu, je to všechno na stejné straně čáry.
-Ovál připouští nanejvýš dvě rovnoběžné tečny.
Příklady
Existuje několik metod konstrukce oválek, které vyžadují použití pravítka, čtverce a kompasu. Poté uvedeme některé z nejpoužívanějších.
Konstrukce oválu pomocí soustředných kruhů
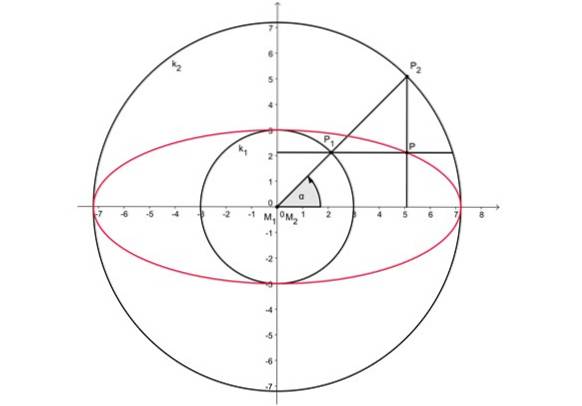
Obrázek 2 výše ukazuje dva soustředné kruhy se středem v počátku. Hlavní osa oválu měří stejně jako průměr vnějšího obvodu, zatímco vedlejší osa odpovídá průměru vnitřního obvodu.
-Na vnější obvod je nakreslen libovolný poloměr, který protíná obě kružnice v bodech P1 A strdva.
-Poté se promítne bod P.dva na vodorovné ose.
-Podobně se promítá bod P.1 na svislé ose.
-Průsečík obou projekčních čar je bod P a patří do oválu.
-Tímto způsobem lze vykreslit všechny body v této části oválu.
-Zbytek oválu lze vysledovat analogickým postupem provedeným v každém kvadrantu.
Výcvik
Dále budou prozkoumány další způsoby konstrukce oválek vzhledem k určitému počátečnímu měření, které určí jejich velikost..
- Cvičení 1
Nakreslete pomocí pravítka a kompasu ovál, známý jako jeho hlavní osa, jehož délka je 9 cm.
Řešení
Na obrázku 3 níže je výsledný ovál zobrazen červeně. Zvláštní pozornost je třeba věnovat tečkovaným čarám, což jsou pomocné konstrukce potřebné k nakreslení oválu, jehož hlavní osa je uvedena. Chystáme se označit všechny nezbytné kroky k dosažení konečného výkresu.
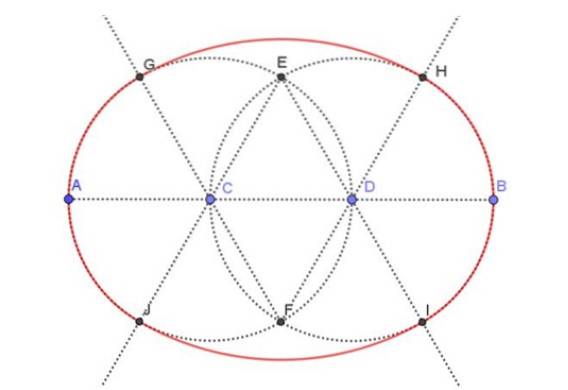
Krok 1
Nakreslete pomocí pravítka segment AB o délce 9 cm.
Krok 2
Trisect segment AB, to znamená, rozdělit jej na tři segmenty stejné délky. Protože původní segment AB je 9 cm, musí segmenty AC, CD a DB měřit každý 3 cm.
Krok 3
S kompasem centrovaným na C a otvorem CA je nakreslen pomocný obvod. Podobně je pomocný obvod se středem D a poloměrem DB nakreslen kompasem..
Krok 4
Průsečíky dvou pomocných kruhů vytvořených v předchozím kroku jsou označeny. Říkáme tomu body E a F.
Krok 5
S pravidlem jsou nakresleny následující paprsky: [FC), [FD), [EC), [ED).
Krok 6
Paprsky předchozího kroku protínají dva pomocné kruhy v bodech G, H, I, J.
Krok 7
Když je střed kompasu vytvořen v F a při otevření (nebo poloměru) FG je oblouk nakreslen GH. Podobně se středem v E a poloměru EI nakreslí oblouk IJ.
Krok 8
Spojení oblouků GJ, JI, IH Y HG tvoří ovál, jehož hlavní osa je 9 cm.
Krok 9
Pokračujeme v mazání (skrývání) pomocných bodů a čar.
- Cvičení 2
Nakreslete ovál pomocí pravítka a kompasu, jehož vedlejší osa je známá a její míra je 6 cm.
Řešení
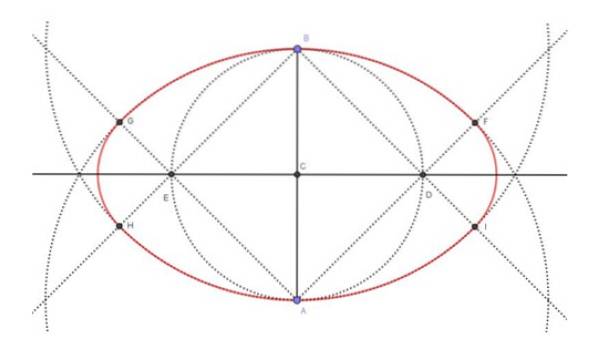
Obrázek nahoře (obrázek 4) ukazuje konečný výsledek konstrukce oválu (červeně) a také mezilehlé konstrukce nezbytné k jeho dosažení. Následující kroky k vytvoření oválné vedlejší osy o průměru 6 cm byly následující:
Krok 1
6 cm dlouhý segment AB je stopován pomocí pravítka.
Krok 2
S kompasem a pravítkem je půlící čára vysledována do segmentu AB.
Krok 3
Průsečík půlové osy se segmentem AB vede ke středu C segmentu AB.
Krok 4
Pomocí kompasu je nakreslen obvod středu C a poloměru CA..
Krok 5
Obvod nakreslený v předchozím kroku protíná půlící část AB v bodech E a D.
Krok 6
Paprsky [AD), [AE], [BD) a [BE) jsou nakresleny.
Krok 7
S kompasem jsou nakresleny obvody středu A a poloměru AB a středu B a poloměru BA..
Krok 8
Průsečíky kruhů nakreslených v kroku 7 s paprsky zkonstruovanými v kroku 6 určují čtyři body, a to: F, G, H, I.
Krok 9
Se středem v D a poloměrem DI je nakreslen oblouk IF. Stejným způsobem se středem v E a poloměrem EG nakreslí oblouk GH.
Krok 10
Spojení obvodových oblouků FG, GH, HI a IF určuje požadovaný ovál.
Reference
- Ed Plastic. Technické křivky: ovály, vejcovody a spirály. Obnoveno z: drajonavarres.wordpress.com.
- Mathematische Basteleien. Vaječné křivky a ovály. Obnoveno z: mathematische-Basteleien.
- University of Valencia. Kónické a ploché technické křivky. Obnoveno z: ocw.uv.es.
- Wikipedia. Ovál. Obnoveno z: es.wikipedia.org.
- Wikipedia. Ovál. Obnoveno z: en.wikipedia.org.



Zatím žádné komentáře