
Vyvažovací vektorový výpočet, příklady, cvičení
The vyrovnávací vektor Je to ten, který je proti výslednému vektoru, a proto je schopen vyvažovat systém, protože má stejnou velikost a stejný směr, ale opačný směr k tomuto.
Vyvažovací vektor mnohokrát odkazuje na vektor síly. Chcete-li vypočítat vyvažovací sílu, nejprve najděte výslednou sílu, jak je znázorněno na následujícím obrázku:
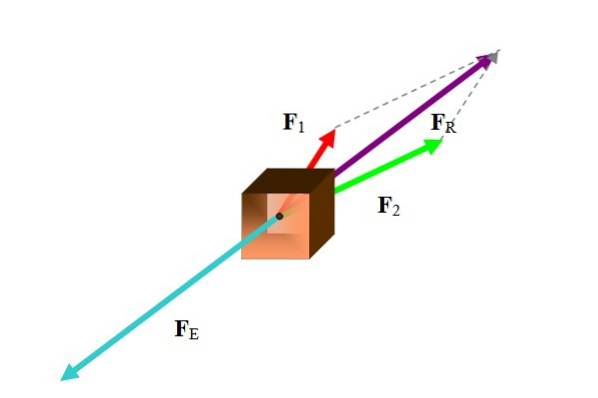
Existují různé způsoby provedení tohoto úkolu v závislosti na dostupných datech. Protože síly jsou vektory, výslednice je vektorový součet zúčastněných sil:
FR = F1 + Fdva + F3 + ... .
Mezi použitými metodami jsou grafické metody jako polygonální, paralelogram a analytické metody, jako je rozklad sil na jejich kartézské složky. V příkladu byla na obrázku použita metoda rovnoběžníku.
Jakmile je výsledná síla nalezena, je vyvažovací síla právě opačný vektor.
Ano FA je vyvažovací síla, pak je uspokojeno, že FA aplikován v určitém bodě, zaručuje translační rovnováhu systému. Pokud se jedná o jedinou částici, nebude se pohybovat (nebo možná bude konstantní rychlostí), ale pokud se jedná o rozšířený objekt, bude mít stále schopnost otáčet:
FR + FA = 0
Rejstřík článků
- 1 Příklady
- 1.1 Tabulka síly
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Příklady
Vyrovnávací síly jsou přítomny všude. Sami jsme vyváženi silou, kterou židle vyvíjí, aby vyrovnala váhu. Objekty, které jsou v klidu: knihy, nábytek, stropní lampy a velké množství mechanismů, jsou neustále vyvažovány silami.
Například kniha v klidu na stole je vyvážena normální silou, kterou působí na knihu a brání jí v pádu. Totéž se děje s řetězem nebo kabelem, který drží lampu visící ze stropu v místnosti. Kabely, které drží břemeno, rozdělují svou váhu prostřednictvím napětí v nich.
V tekutině jsou některé předměty schopné plavat a zůstat v klidu, protože jejich váha je vyvážena vzestupnou silou vyvíjenou kapalinou, tzv. tam.
Je třeba vyvážit různé mechanismy, které znají vektor vyvažovací síly, jako jsou pruty, nosníky a sloupy.
Při použití stupnice je nutné nějakým způsobem vyvážit váhu objektu se silou, která je ekvivalentní, buď přidáním závaží nebo pomocí pružin..
Tabulka síly
Tabulka síly se používá v laboratoři k určení vyvažovací síly. Skládá se z kruhové plošiny, na kterou máte na obrázku pohled shora a která má úhloměr k měření úhlů.
Na okrajích stolu jsou kladky, kterými procházejí lana, která drží závaží a která se sbíhají v kruhu, který je uprostřed.
Například jsou zavěšena dvě závaží. Napětí generovaná v řetězcích těmito váhami jsou nakreslena červeně a modře na obrázku 2. Třetí závaží v zelené barvě může vyvážit výslednou sílu dalších dvou a udržovat systém v rovnováze..
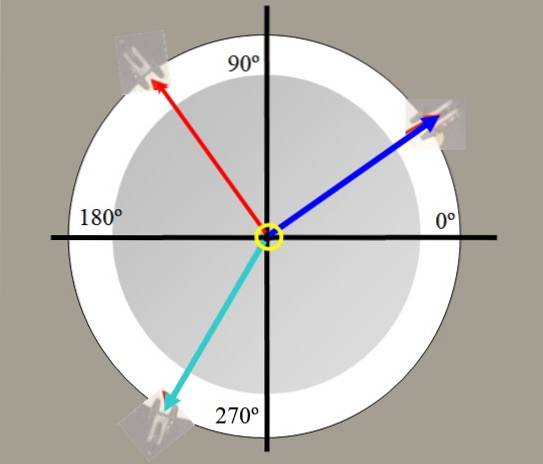
Pomocí silové tabulky je možné ověřit vektorový charakter sil, rozložit síly, najít vyrovnávací sílu a ověřit Lamyho větu:
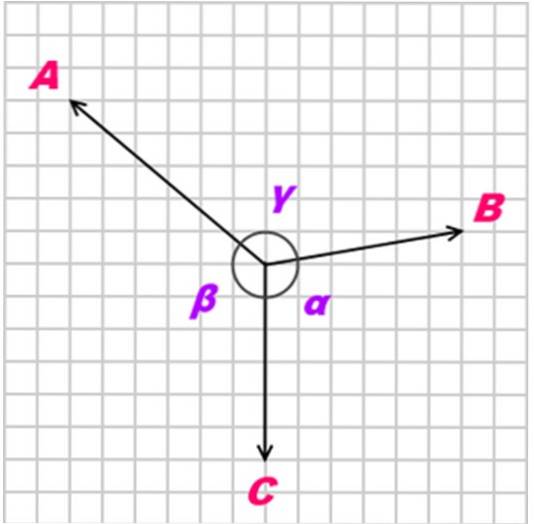
Pokud těleso je v rovnováze díky třem koplanárním silám, souběžným a nekolineárním (ne paralelním), tzv. NA, B Y C, vztah mezi těmito silami je následující:
A / sin α = B / sin β = C / sin γ
Vyřešená cvičení
-Cvičení 1
Hmotnosti 225 g (modré napětí) a 150 g (červené napětí) jsou zavěšeny na silovém stole na obrázku 2 se znázorněnými úhly. Najděte hodnotu vyvažovací síly a úhel, který svírá se svislou osou.
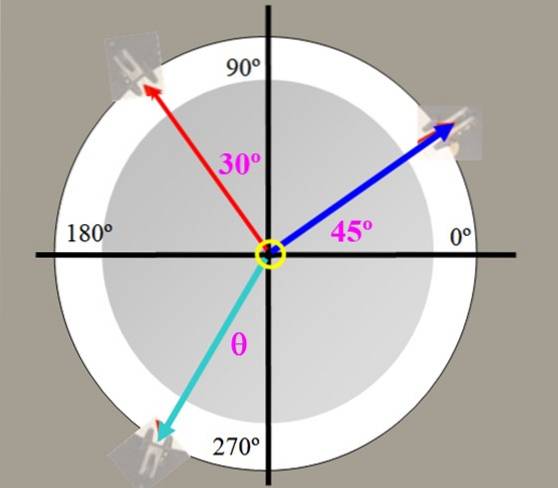
Řešení
Na problému lze pracovat s váhami vyjádřenými v gramech (síly). Ať P1 = 150 gramů a Pdva = 225 gramů, příslušné složky každého z nich jsou:
P1x = 225. cos 45 ° g = 159,10 g; P1 rok = 225. cos 45º g = 159,10 g
P2x = -150. hřích 30 g = -75,00 g; P2 a = 150. cos 30º g = 129,90 g
Výsledná hmotnost PR je nalezen algebraickým přidáním komponent:
PRx = 159,10 - 75,00 g = 84,10 g
PRy = 159,10 + 129,90 g = 289,00 g
Vyvažovací závaží PA je vektor naproti PR:
PBývalý = -84,10 g
PAhoj = -289,00 g
Velikost vyvažovacího závaží se vypočítá z:
PA = (StrBývalýdva + PAhojdva)1/2 = ((-84,10)dva + (-289,00)dva)1/2 g = 301 g
Úhel θ na obrázku je:
θ = arctg (-84,10 / -289,00) = 16,2 ° vzhledem k ose Y záporný.
-Cvičení 2
Najděte vyvažovací vektor systému, který je znázorněn na obrázku, s vědomím, že každý čtverec měří ze strany 10 m.
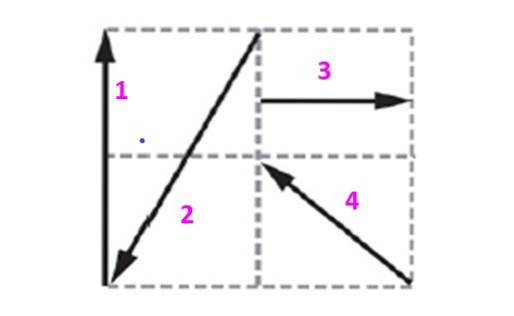
Řešení
Vektory obsažené v této mřížce budou vyjádřeny jednotkovými a ortogonálními vektory i Y j které určují rovinu. Vektor 1, který bude označen jako proti1 má velikost 20 ma směřuje svisle nahoru. Lze jej vyjádřit jako:
proti1 = 0 i +dvacet j m
Z výkresu je vidět, že vektor 2 je:
protidva = -10 i - dvacet j m
Vektor 3 je vodorovný a ukazuje v pozitivním směru:
proti3 = 10 i + 0 j m
Nakonec je vektor 4 nakloněn o 45 °, protože jde o úhlopříčku čtverce, proto jeho součásti měří stejně:
proti4 = -10 i + 10 j m
Všimněte si, že značky označují, ke které straně osy jsou komponenty: nahoře a napravo mají znaménko +, zatímco dole a nalevo mají znaménko -.
Výsledný vektor se získá přidáním komponenty ke komponentě:
protiR = -10 i + 10 j m
Vyvažovací vektor systému je pak:
protiA = 10 i - 10 j m
Reference
- Beardon, T. 2011. Úvod do vektorů. Citováno z: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Fyzika pro vědy a inženýrství. Svazek 1. Kinematika. 31-68.
- Fyzický. Modul 8: Vektory. Obnoveno z: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanics for Engineers. Statický. 6. vydání. Continental Publishing Company. 15-53.
- Kalkulačka sčítání vektorů. Obnoveno z: 1728.org
- Vektory. Obnoveno z: wikibooks.org


Zatím žádné komentáře