
Vzorce průměrné rychlosti, způsob výpočtu a vyřešení cvičení
The průměrná rychlost pro mobilní částice je definována jako poměr mezi změnou polohy, kterou zažívá, a časovým intervalem použitým při změně. Nejjednodušší situace je situace, kdy se částice pohybuje po přímce představované osou x..
Předpokládejme, že pohybující se objekt zaujímá pozice x1 a xdva v dobách t1 a tydva resp. Definice průměrné rychlosti protim je matematicky znázorněno takto:

Jednotky protim v mezinárodním systému jsou to metry za sekundu (m / s). Další běžně používané jednotky, které se objevují v textech a mobilních zařízeních, jsou: km / h, cm / s, míle / h, stopy / s a další, pokud jsou délky / času formuláře.
Řecké písmeno „Δ“ se čte „delta“ a používá se ke krátkému označení rozdílu mezi dvěma veličinami..
Rejstřík článků
- 1 Charakteristiky vektoru střední rychlosti vm
- 2 Známky průměrné rychlosti
- 3 Průměrná rychlost: skalární veličina
- 4 Cvičení vyřešeno
- 5 Reference
Charakteristiky vektoru střední rychlosti vm

Průměrná rychlost je vektor, protože souvisí se změnou polohy, která je zase známá jako svitek vektor.
Tato kvalita je vyjádřena tučně nebo šipkou nad písmenem, které označuje velikost. V jedné dimenzi je však jediným možným směrem směr osy x, a proto lze od vektorového zápisu upustit.
Protože vektory mají velikost, směr a smysl, počáteční pohled na rovnici naznačuje, že průměrná rychlost bude mít stejný směr a smysl jako posunutí..
Představte si, že by se částice v příkladu pohybovala po přímce. K popisu jejího pohybu je nutné uvést referenční bod, kterým bude „počátek“ a bude označen jako O.
Částice se může pohybovat směrem k O nebo od něj, buď doleva nebo doprava. Získání určité polohy může také trvat dlouho nebo krátce..
Zmíněné veličiny: poloha, posunutí, časový interval a průměrná rychlost, popisují chování částice při jejím pohybu. Jde o veličiny kinematika.
K rozlišení pozic nebo umístění nalevo od O se používá znak (-) a ty napravo od O nesou znak (+).
Průměrná rychlost má geometrickou interpretaci, kterou lze vidět na následujícím obrázku. Je to sklon přímky, která prochází body P a Q. Při řezání polohy křivky vs. čas ve dvou bodech, je to přímka sušení.
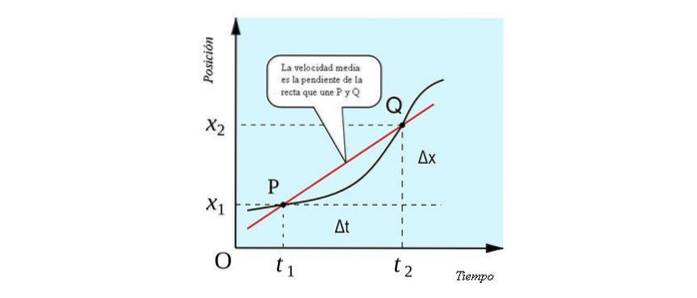
Známky průměrné rychlosti
Pro následující analýzu je třeba vzít v úvahu, že tdva > t1. To znamená, že další okamžik je vždy větší než ten aktuální. Takto tdva - t1 je vždy pozitivní, což obvykle dává každý den smysl.
Potom bude znaménko střední rychlosti určeno znaménkem Xdva - X1. Všimněte si, že je důležité si ujasnit, kde je bod O - původ - protože jde o bod, ve kterém se říká, že částice jde „doprava“ nebo „doleva“.
Buď „vpřed“, nebo „vzad“, jak dává přednost čtenáři.
Pokud je střední rychlost kladná, znamená to v průměru hodnota "X„Zvyšuje se v průběhu času, i když to neznamená, že se v určitém okamžiku uvažovaného časového období mohlo snížit. - Δt -.
Globálně však na konci věků Δt, skončila s větší pozicí, než měla na začátku. Podrobnosti o pohybu jsou v této analýze ignorovány..
Co když se ukáže, že průměrná rychlost bude záporná? Pak to znamená, že částice končí s menší souřadnicí než ta, se kterou začala. Zhruba se vrátil. Podívejme se na několik numerických příkladů:
Příklad 1: Vzhledem k vyznačené počáteční a koncové poloze uveďte znaménko průměrné rychlosti. Kam se částice globálně posunula??
a) x1 = 3 m; Xdva = 8 m
Odpovědět: Xdva- X1 = 8 m - 3 m = 5 m. Pozitivní střední rychlost, částice se pohybovala dopředu.
b) x1 = 2 m; Xdva = -3 m
Odpovědět: Xdva - X1 = -3 m - 2 m = -5 m. Záporná střední rychlost, částice se pohnula dozadu.
c) x1 = - 5 m; Xdva = -12 m
Odpovědět: Xdva - X1 = -12 m - (-5 m) = -7 m. Záporná střední rychlost, částice se pohnula dozadu.
d) x1 = - 4 m; Xdva = 10 m
Odpovědět: Xdva - X1 = 10 m - (-4 m) = 14 m. Pozitivní střední rychlost, částice se pohybovala dopředu.
Může být průměrná rychlost 0? Ano, pokud je výchozí bod a bod příjezdu stejný. Znamená to, že částice byla nutně po celou dobu v klidu??
Ne, znamená to jen, že cesta byla zpáteční. Možná cestoval rychle nebo možná velmi pomalu. Zatím to není známo.
Průměrná rychlost: skalární veličina
To nás vede k definování nového pojmu: střední rychlost. Ve fyzice je důležité rozlišovat mezi vektorovými veličinami a nevektorovými veličinami: skaláry.
U částice, která způsobila okružní cestu, je průměrná rychlost 0, ale mohla nebo nemusí být velmi rychlá. Chcete-li zjistit, střední rychlost je definována jako:

Jednotky pro průměrnou rychlost jsou stejné jako jednotky pro průměrnou rychlost. Základní rozdíl mezi oběma veličinami je v tom, že průměrná rychlost zahrnuje zajímavé informace o směru a smyslu částice..
Na druhou stranu průměrná rychlost poskytuje pouze číselné informace. S ním je známo, jak rychle nebo pomalu se částice pohybovala, ale ne pokud se pohybovala dopředu nebo dozadu. Jde tedy o skalární velikost. Jak je rozlišit, když je označujeme? Jedním ze způsobů je ponechat tučné tuky pro vektory nebo umístit na ně šipku.
A je důležité si uvědomit, že průměrná rychlost se nemusí rovnat průměrné rychlosti. Pro zpáteční let je průměrná rychlost nulová, ale průměrná rychlost není. Oba mají stejnou číselnou hodnotu, když cestujete vždy stejným směrem.
Cvičení vyřešeno
Jedete zpět domů ze školy v klidu rychlostí 95 km / h po dobu 130 km. Začíná pršet a zpomaluje na 65 km / h. Nakonec se vrátí domů po 3 hodinách a 20 minutách jízdy.
a) Jak daleko jste doma od školy?
b) Jaká byla průměrná rychlost?
Odpovědi:
a) Je nutné provést několik předběžných výpočtů:
Cesta je rozdělena na dvě části, celková vzdálenost je:
d = d1 + ddva, s d1 = 130 km


t2 = 3,33 - 1,37 hodiny = 1,96 hodiny
Výpočet ddva:
ddva = 65 km / h x 1,96 h = 125,4 km.
Škola je vzdálená d1 + ddva = 255,4 km od domova.
b) Nyní můžeme najít střední rychlost:


Reference
- Giancoli, D. Fyzika. Zásady s aplikacemi. Šesté vydání. Prentice Hall. 21-22.
- Resnick, R. (1999). Fyzický. Svazek 1. Třetí vydání ve španělštině. Mexiko. Compañía Editorial Continental S.A. de C.V. 20-21.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7ma. Edice. Mexiko. Cengage Learning Editors. 21-23.



Zatím žádné komentáře