
Axiální zatížení, jak se počítá a cvičení řeší
The axiální zatížení Je to síla, která je směrována rovnoběžně s osou symetrie prvku, který tvoří strukturu. Axiální silou nebo zatížením může být napětí nebo tlak. Pokud se linie působení axiální síly shoduje s osou symetrie, která prochází těžiště uvažovaného prvku, pak se říká, že jde o soustředné axiální zatížení nebo sílu.
Naopak, pokud se jedná o axiální sílu nebo zatížení rovnoběžné s osou symetrie, ale jehož linie působení není na samotné ose, jedná se o excentrickou axiální sílu.
-
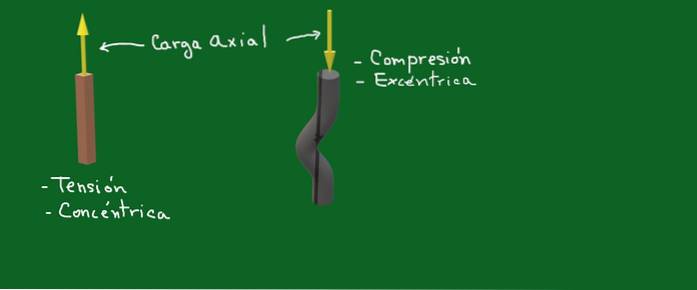
Obrázek 1. Axiální zatížení. Zdroj: vlastní výroba
Na obrázku 1 představují žluté šipky axiální síly nebo zatížení. V jednom případě se jedná o koncentrickou napínací sílu a ve druhém máme co do činění s excentrickou kompresní silou.
Jednotkou měření axiálního zatížení v mezinárodním systému SI je Newton (N). Ale často se používají i jiné jednotky síly, jako je kilogram síla (kg-f) a síla libry (lb-f)..
Rejstřík článků
- 1 Jak se počítá?
- 1.1 Vztah axiálního zatížení s normálovým napětím
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Jak se to počítá?
Pro výpočet hodnoty osového zatížení v prvcích konstrukce je třeba dodržet následující kroky:
- Na každém prvku vytvořte silový diagram.
- Aplikujte rovnice, které zaručují translační rovnováhu, to znamená, že součet všech sil je nula.
- Zvažte rovnici momentů nebo momentů tak, aby byla splněna rotační rovnováha. V takovém případě musí být součet všech momentů nulový.
- Vypočítejte síly a určete síly nebo axiální zatížení v každém z prvků.
Poměr axiálního zatížení k normálnímu napětí
Průměrné normální napětí je definováno jako poměr axiálního zatížení děleno plochou průřezu. Jednotky normálního úsilí v mezinárodním systému S.I. jsou to Newton přes metr čtvereční (N / m²) nebo Pascal (Pa). Následující obrázek 2 ilustruje koncept normálního napětí pro jasnost..
-
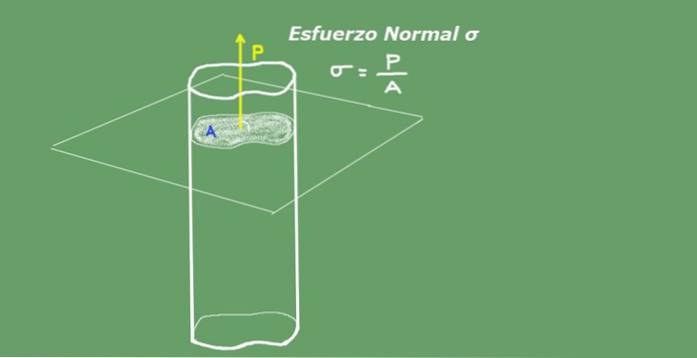
Obrázek 2. Normální napětí. Zdroj: vlastní výroba.
Vyřešená cvičení
-Cvičení 1
Vezměme si válcový betonový sloup o výšce h a poloměru r. Předpokládejme, že hustota betonu je ρ. Sloup nepodporuje žádné další zatížení kromě své vlastní hmotnosti a je nesen na obdélníkové základně.
- Najděte hodnotu axiálního zatížení v bodech A, B, C a D, které jsou v následujících polohách: A ve spodní části sloupu, B a ⅓ výšky h, C a ⅔ výšky h a poslední D v horní část sloupce.
- Určete také průměrné normální napětí v každé z těchto pozic. Vezměte následující číselné hodnoty: h = 3m, r = 20cm a ρ = 2250 kg / m³
-
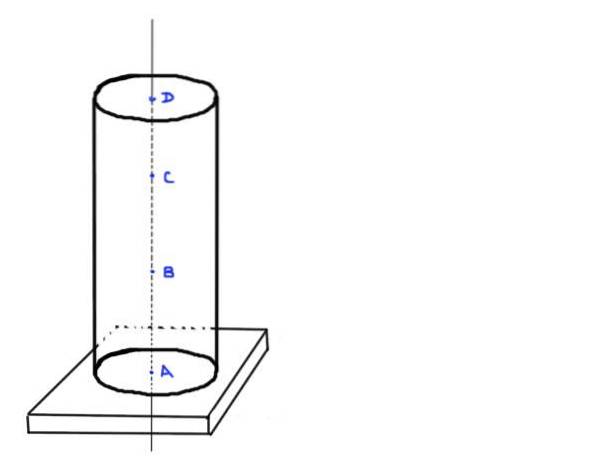
Obrázek 3. Válcový sloup. Zdroj: vlastní výroba.
Řešení
Celková hmotnost sloupce
Celková hmotnost W kolony je součinem její hustoty a objemu vynásobeného gravitačním zrychlením:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Axiální zatížení v A
V bodě A musí sloup podporovat jeho plnou hmotnost, takže axiální zatížení v tomto bodě je komprese se rovná hmotnosti sloupu:
PA = W = 8313 N
Axiální zatížení při B
Pouze ⅔ sloupu bude v bodě B, takže axiální zatížení v tomto bodě bude komprese a jeho hodnota ⅔ hmotnost sloupu:
PB = ⅔ W = 5542 N
Obrázek 3. Válcový sloup. Zdroj: vlastní výroba.
Nad pozicí C je pouze ⅓ sloupu, takže jeho axiální zatížení v tlaku bude ⅓ jeho vlastní hmotnosti:
PC = ⅓ W = 2771 N.
Axiální zatížení v D
Nakonec v bodě D, který je horním koncem sloupu, nedochází k žádnému zatížení, takže axiální síla v tomto bodě je nulová..
PD = 0 N.
Normální úsilí v každé z pozic
Pro určení normálového napětí v každé z poloh bude nutné vypočítat průřez oblasti A, který je dán vztahem:
A = π ∙ r² = 0,126m²
Tímto způsobem bude normální napětí v každé z poloh kvocient mezi osovou silou v každém z bodů dělenou již vypočítanou plochou průřezu, která je v tomto cvičení pro všechny body stejná, protože se jedná o sloupec válcový.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Cvičení 2
Obrázek ukazuje strukturu tvořenou dvěma pruhy, které budeme nazývat AB a CB. Lišta AB je na konci A podepřena kolíkem a na druhém konci spojena s druhou lištou jiným kolíkem B..
Podobně je tyč CB podepřena na konci C pomocí čepu a na konci B čepem B, který ji spojuje s druhou tyčí. Na čep B působí svislá síla nebo zatížení F, jak je znázorněno na následujícím obrázku:
-
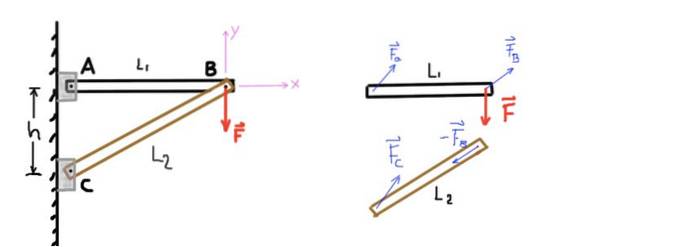
Obrázek 4. Struktura dvou sloupců a diagram volného těla. Zdroj: vlastní výroba.
Předpokládejme, že hmotnost tyčí bude zanedbatelná, protože síla F = 500 kg-f je mnohem větší než hmotnost konstrukce. Vzdálenost mezi podpěrami A a C je h = 1,5 ma délka tyče AB je L1 = 2 m. Určete axiální zatížení na každé z tyčí a určete, zda se jedná o axiální zatížení v tlaku nebo v tahu.
Řešení 2
Obrázek ukazuje pomocí diagramu volného těla síly působící na každý z prvků konstrukce. Rovněž je uveden kartézský souřadný systém, se kterým budou stanoveny rovnice silové rovnováhy..
Momenty nebo momenty se vypočítají v bodě B a budou považovány za pozitivní, pokud směřují od obrazovky (osa Z). Rovnováha sil a momentů pro každý sloupec je:
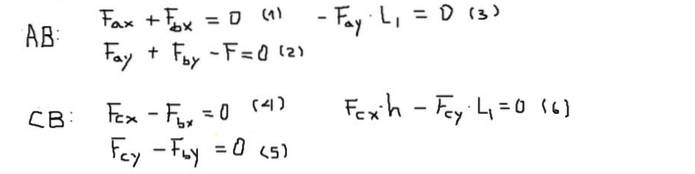
Dále jsou složky sil každé z rovnic řešeny v následujícím pořadí:
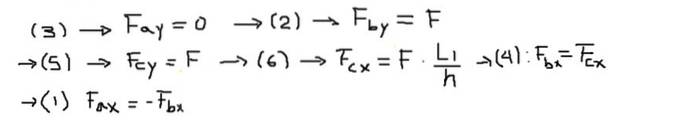
Nakonec se vypočítají výsledné síly na koncích každé tyče:
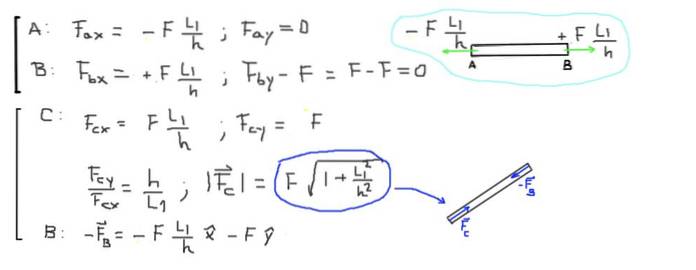
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
Prut CB je v tlaku díky dvěma silám působícím na jeho koncích, které jsou rovnoběžné s prutem a směřují k jeho středu. Velikost axiální kompresní síly v tyči CB je:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Reference
- Pivo F… Mechanika materiálů. 5. Edice. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mechanika materiálů. Osmé vydání. Prentice Hall. 2011. 3-60.
- Gere J. Mechanika materiálů. Osmé vydání. Cengage Learning. 4-220.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6. vyd. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Poznámky k obecné fyzice. UNAM. 87-98.



Zatím žádné komentáře