
Shoda kongruentní čísla, kritéria, příklady, cvičení
The shoda, V geometrii to poukazuje na to, že pokud mají dvě rovinné postavy stejný tvar a rozměry, jsou shodné. Například dva segmenty jsou shodné, když jsou jejich délky stejné. Podobně mají shodné úhly stejnou míru, i když nejsou v rovině orientovány stejným způsobem..
Termín „shoda“ pochází z latiny shodný, jehož význam je korespondence. Dvě shodné postavy si tedy přesně odpovídají..
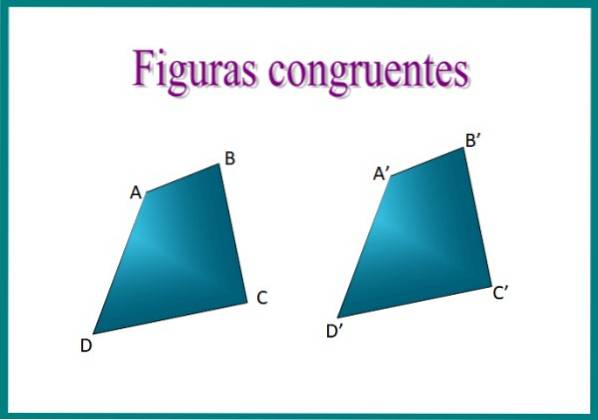
Například pokud překryjeme dva čtyřúhelníky v obrázku, zjistíme, že jsou shodné, protože uspořádání jejich stran je identické a měří stejné.
Umístěním čtyřúhelníků ABCD a A'B'C'D 'na sebe budou čísla přesně odpovídat. Jsou vyvolány odpovídající strany homologní strany nebo odpovídající a pro vyjádření shodnosti se používá symbol ≡. Pak můžeme konstatovat, že ABCD ≡ A'B'C'D '.
Rejstřík článků
- 1 Kritéria shody
- 1.1 Shodnost, identita a podobnost
- 2 Příklady shody
- 2.1 - Úhlová kongruence
- 2.2 - Shoda trojúhelníků
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Kritéria shody
Následující vlastnosti jsou společné pro shodné polygony:
-Stejný tvar a velikost.
-Identické míry jejich úhlů.
-Stejná míra na každé z jeho stran.
V případě, že dva dotyčné polygony jsou pravidelné, to znamená, že všechny strany a vnitřní úhly měří stejně, je zajištěna shoda, když jsou splněny nějaký následujících podmínek:
-Boky jsou shodné
-The apothemy mají stejnou míru
-The rádio každého polygonu měří stejně
Apothem pravidelného mnohoúhelníku je vzdálenost mezi středem a jednou ze stran, zatímco poloměr odpovídá vzdálenosti mezi středem a vrcholem nebo rohem obrázku.
Kritéria shody se často používají, protože tolik dílů a dílů všeho druhu se vyrábí hromadně a musí mít stejný tvar a rozměry. Tímto způsobem je lze v případě potřeby snadno vyměnit, například matice, šrouby, plechy nebo dlažební kameny na zemi na ulici..

Shodnost, identita a podobnost
Existují například geometrické pojmy související s kongruencí stejné údaje a podobné údaje, to nutně neznamená, že čísla jsou shodná.
Všimněte si, že shodné obrazce jsou identické, avšak čtyřúhelníky na obrázku 1 by mohly být v rovině orientovány různými způsoby a stále zůstávat shodné, protože odlišná orientace nemění velikost jejich stran ani jejich úhlů. V takovém případě by přestali být totožní.
Druhým konceptem je podobnost obrázků: dvě rovinné postavy jsou podobné, pokud mají stejný tvar a jejich vnitřní úhly se měří stejně, i když velikost obrázků se může lišit. V takovém případě nejsou údaje shodné.
Příklady shody
- Shoda úhlu
Jak jsme naznačili na začátku, shodné úhly mají stejnou míru. Existuje několik způsobů, jak získat shodné úhly:
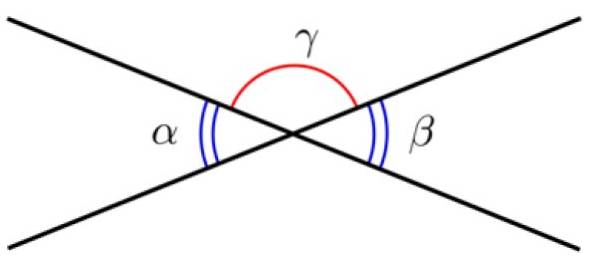
Příklad 1
Dvě přímky se společným bodem definují dva úhly, tzv Opačné úhly vrcholem. Tyto úhly mají stejnou míru, a proto jsou shodné.
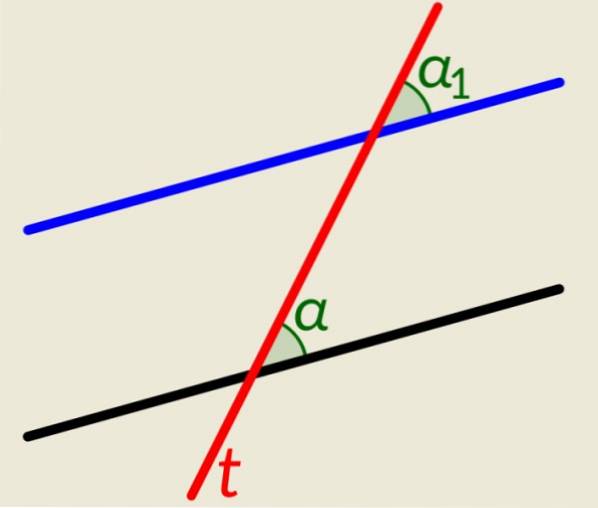
Příklad 2
Existují dvě paralelní linie plus jedna linie t který je protíná oba. Stejně jako v předchozím příkladu, když tato čára protíná rovnoběžky, generuje shodné úhly, jeden na každém řádku na pravé straně a další dva na levé straně. Obrázek ukazuje α a α1, napravo od čáry t, které jsou shodné.
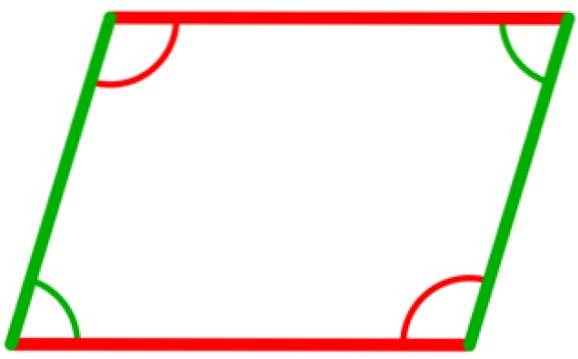
Příklad 3
V rovnoběžníku jsou čtyři vnitřní úhly, které jsou shodné dva až dva. Jsou to ty, které jsou mezi protilehlými vrcholy, jak je znázorněno na následujícím obrázku, ve kterém jsou dva úhly zelené shodné, stejně jako dva úhly červené.
- Shoda trojúhelníků
Dva trojúhelníky stejného tvaru a velikosti jsou shodné. Chcete-li to ověřit, existují tři kritéria, která lze zkoumat při hledání shody:
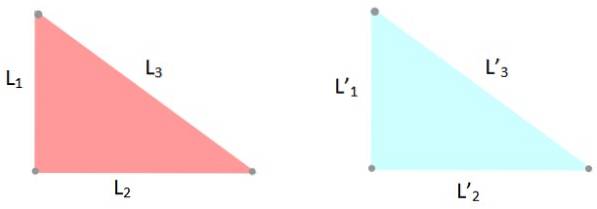
-Kritérium LLL: tři strany trojúhelníků mají stejná měření, proto L1 = L '1; Ldva = L 'dva a L.3 = L '3.
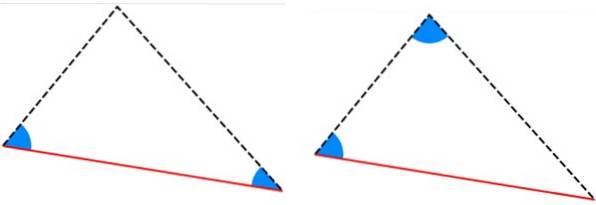
-Kritéria ALA a AAL: trojúhelníky mají dva stejné vnitřní úhly a strana mezi těmito úhly má stejnou míru.
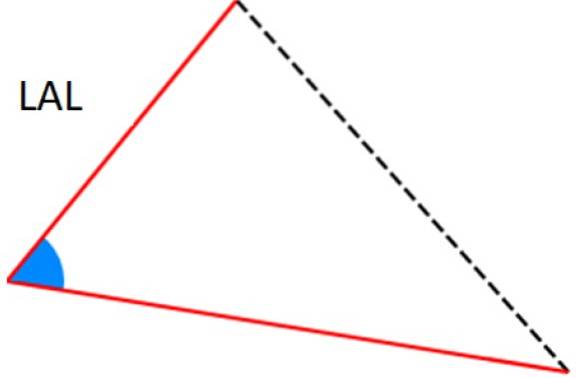
-Kritérium LAL: dvě strany jsou identické (odpovídající) a mezi nimi je stejný úhel.
Vyřešená cvičení
- Cvičení 1
Na následujícím obrázku jsou znázorněny dva trojúhelníky: ΔABC a ΔECF. Je známo, že AC = EF, že AB = 6 a že CF = 10. Dále jsou úhly ∡BAC a ∡FEC shodné a úhly ∡ACB a ∡FCB jsou rovněž shodné..
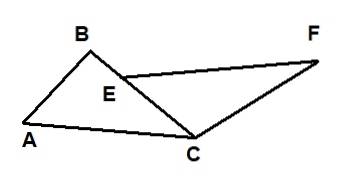
Pak se délka segmentu BE rovná:
i) 5
ii) 3
(iii) 4
(iv) 2
(v) 6
Řešení
Protože dva trojúhelníky mají stranu se stejnou délkou AC = EF složenou ze stejných úhlů ∡BAC = ∡CEF a ∡BCA = ∡CFE, lze říci, že tyto dva trojúhelníky odpovídají kritériu ALA.
To znamená, ΔBAC ≡ ΔCEF, takže musíme:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Vypočítaný segment je však BE = BC - EC = 10 - 6 = 4.
Správná odpověď je tedy (iii).
- Cvičení 2
Na obrázku níže jsou znázorněny tři trojúhelníky. Je také známo, že dva uvedené úhly měří každý 80 ° a že segmenty AB = PD a AP = CD. Najděte hodnotu úhlu X uvedenou na obrázku.
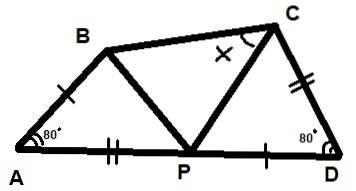
Řešení
Musíte použít vlastnosti trojúhelníků, které jsou podrobně popsány krok za krokem.
Krok 1
Počínaje kritériem shodnosti trojúhelníku LAL lze konstatovat, že trojúhelníky BAP a PDC jsou shodné:
ΔBAP ≡ ΔPDC
Krok 2
Výše uvedené vede k potvrzení, že BP = PC, proto je trojúhelník ΔBPC rovnoramenný a ∡PCB = ∡PBC = X.
Krok 3
Pokud nazýváme úhel BPC γ, vyplývá z toho, že:
2x + γ = 180 °
Krok 4
A pokud nazýváme úhly APB a DCP β a α úhly ABP a DPC, máme:
α + β + γ = 180 ° (protože APB je rovinný úhel).
Krok 5
Dále α + β + 80º = 180º součtem vnitřních úhlů trojúhelníku APB.
Krok 6
Spojením všech těchto výrazů máme:
α + β = 100 °
Krok 7
A proto:
γ = 80 °.
Krok 8
Nakonec z toho vyplývá, že:
2X + 80º = 180º
S X = 50 °.
Reference
- Baldor, A. 1973. Geometrie roviny a prostoru. Středoamerický kulturní.
- Nadace CK-12. Shodné polygony. Obnoveno z: ck 12.org.
- Užijte si matematiku. Definice: Poloměr (mnohoúhelník). Obnoveno z: gustolasmatematicas.com.
- Matematická otevřená reference. Testování polygonů na shodu. Obnoveno z: mathopenref.com.
- Wikipedia. Shodnost (geometrie). Obnoveno z: es.wikipedia.org.
- Zapata, F. Trojúhelníky, historie, prvky, klasifikace, vlastnosti. Obnoveno z: lifeder.com.

Zatím žádné komentáře